Дано 3 нечетких множества A, B, C (заданы их функции принадлежности). Построить функцию принадлежности нечеткого множества 
и определить степень принадлежности одного элемента множеству D, используя метод ограничений.
t = 0:0.01:20; % определяем число значений по оси абсцисс
a=2; b=8; c=13; %Параметры функции принадлежности М_А
a1=3; b1=5; %Параметры функции принадлежности М_В
a2=2; b2=8; c2=9; d2=14; %Параметры функции принадлежности М_С
% Рассчитываем значения оси ординат функций принадлежности М_А, М_B, М_C
j=1;
for i = 0:0.01:20
if i<=a M_A(j)=0;
elseif (i>a)&(i<=b) M_A(j)=0.5*(i-a)/(b-a);
elseif (i>b)&(i<=c) M_A(j)=0.5*(c-i)/(c-b);
elseif (i>c) M_A(j)=0; end;
if i<=a1 M_B(j)=0;
elseif (i>a1)&(i<=b1) M_B(j)=(i-a1)/(b1-a1);
elseif (i>b1) M_B(j)=1; end;
if i<=a2 M_C(j)=0;
elseif (i>a2)&(i<=b2) M_C(j)=0.5*(i-a2)/(b2-a2);
elseif (i>b2)&(i<=c2) M_C(j)=-0.25*i+2.5;
elseif (i>c2)&(i<=d2) M_C(j)=0.25*(d2-i)/(d2-c2);
elseif (i>d2) M_C(j)=0; end
j=j+1;
end;
% Строим график функции принадлежности М_А, М_B, М_C
subplot(2, 3, 1)
plot(t, M_A, 'LineWidth', 4); grid on; xlabel('X'); ylabel('M_A(x)');
subplot(2, 3, 2)
plot(t, M_B, 'LineWidth', 4); grid on; xlabel('X'); ylabel('M_B(x)');
subplot(2, 3, 3)
plot(t, M_C, 'LineWidth', 4); grid on; xlabel('X'); ylabel('M_C(x)');
Описание процесса решения. Для построения функции принадлежности нового множества необходимо:
1) Определить последовательность выполнения операций в формуле.
2) Построить на отдельных графиках промежуточные множества, согласно определенной последовательности действий. Свести промежуточные множества на одном графике и определить итоговую функцию принадлежности.
3) Используя определенный в задаче метод, определить аналитически степень принадлежности элемента, входящего в ядро итогового множества.
4) Проверить аналитические вычисления по построенному графику функции принадлежности.
Решение.
1) Множество 
, значит, последовательность операций будет следующей: 
.
% Рассчитываем значения последовательности операций
j=1;
for i = 0:0.01:20
M_n_A(j)=1-M_A(j); % Рассчитываем значение отрицания А (M_n_A)
if (M_A(j)+M_B(j))<1 M_A_B(j)=M_A(j)+M_C(j); else M_A_B(j)=1; end;% Рассчитываем значение объединения А и В (M_A_B)
if (M_A_B(j)+M_C(j))<1 M_A_B_C(j)=M_A_B(j)+M_C(j); else M_A_B_C(j)=1; end; %Рассчитываем значение объединения (M_A_B_C)
if (M_A_B_C(j)+M_n_A(j)-1)>0 M_D(j)=M_A_B_C(j)+M_n_A(j)-1; else M_D(j)=0; end; % Рассчитываем значение M_D
j=j+1;
end;
2) Построим согласно этой последовательности операций графики функций принадлежности:
% Строим графики функций рассчитанных функций принадлежности
subplot(2, 3, 4)
plot(t, M_n_A, 'LineWidth', 4); grid on; xlabel('X'); ylabel('M_n_A(X)');
subplot(2, 3, 5)
plot(t, M_A_B_C, 'LineWidth', 4); grid on; xlabel('X'); ylabel('M_A_B_C(X)');
subplot(2, 3, 6)
plot(t, M_D, 'LineWidth', 4); grid on; xlabel('X'); ylabel('M_D(X)');
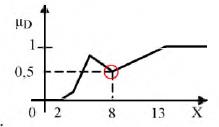
3) Носитель множества D состоит из элементов из интервала [2, 15]. Ядро множества D состоит из элементов [13, 14, 15]. Выберем элемент 8.
4) 
Контрольные вопросы к защите
1. Каким образом задается нечеткое множество?
2. Назовите операции над нечеткими множествами?
3. Что такое функция принадлежности?
4. Каким образом задается функция принадлежности?
5. Может ли функция принадлежности изменяться в интервале [-1, +1]?
