Лабораторная работа №2. Использование нечетких операций при построении функции принадлежности
Цель работы: Изучить операции, выполняемые над нечеткими множествами.
Теоретическая часть
Нечеткие множества и нечеткая логика
С точки зрения характеристической функции, нечеткие множества есть естественное обобщение обычных множеств, когда мы отказываемся от бинарного характера этой функции и предполагаем, что она может принимать любые значения на отрезке [0, 1]. В теории нечетких множеств характеристическая функция называется функцией принадлежности, а ее значение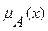 
— степенью принадлежности элемента 
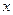нечеткому множеству 
.
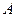Более строго, нечетким множеством 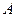называется совокупность пар
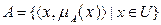
где 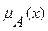— функция принадлежности, т.е. 
.
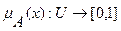Операции над нечеткими множествами
Над нечеткими множествами можно производить различные операции, при этом необходимо определить их так, чтобы в частном случае, когда множество является четким, операции переходили в обычные операции теории множеств, то есть операции над нечеткими множествами должны обобщать соответствующие операции над обычными множествами. При этом обобщение может быть реализовано различными способами, из-за чего какой-либо операции над обычными множествами может соответствовать несколько операций в теории нечетких множеств. Для определения пересечения и объединения нечетких множеств наибольшей популярностью пользуются следующие три группы операций:
1. Максиминные:
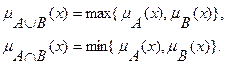
2. Алгебраические:
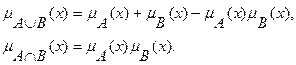
3. Ограниченные:
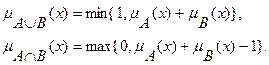
Дополнение нечеткого множества во всех трех случаях определяется одинаково: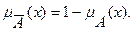 
Более детально представление операций над нечеткими множествами представлено в теме 2 настоящего учебного пособия.
Кусочно-линейные функции принадлежности
Наиболее характерным примером таких функций являются "треугольная" (рисунок 2.1, а) и "трапециевидная" (рисунок 2.1, б) функции принадлежности.
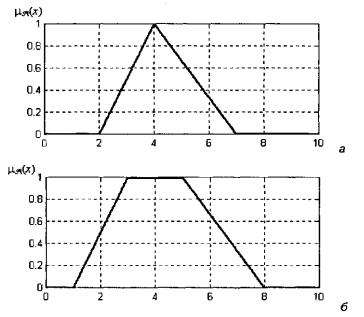
Рисунок 2.1 - Графики функций принадлежности треугольной (а)
и трапециевидной (б) формы
Первая из этих функций принадлежности в общем случае может быть задана аналитически следующим выражением:
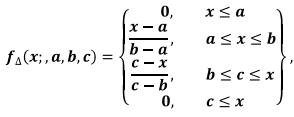
где a, b, с — некоторые числовые параметры, принимающие произвольные действительные значения и упорядоченные отношением: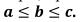 
Как нетрудно заметить, параметры a и c характеризуют основание треугольника, а параметр b — его вершину.
Трапециевидная функция принадлежности в общем случае может быть задана аналитически следующим выражением:
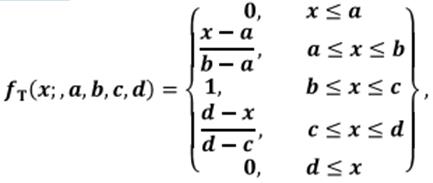
где а, b, с, d— некоторые числовые параметры, принимающие произвольные действительные значения и упорядоченные отношением: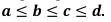 
В качестве частных случаев Z- и S-образных кривых удобно рассматривать так называемую линейную Z-образную функцию (рисунок 2.2, а) и линейную S-образную функцию (рисунок 2.2, б). Первая из этих функций в общем случае может быть задана аналитически следующим выражением:
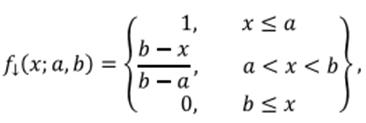
где а, b — некоторые числовые параметры, принимающие произвольные действительные значения и упорядоченные отношением: а<b.
Вторая из этих функций в общем случае может быть задана аналитически следующим выражением:
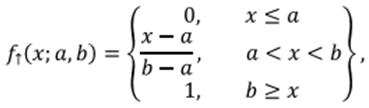
где a, b — некоторые числовые параметры, принимающие произвольные действительные значения и упорядоченные отношением: а<b.
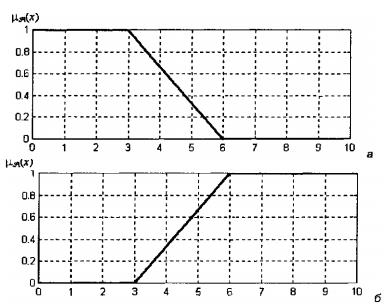
Рисунок 2.2 - Графики линейной Z-образной функции (а) и линейной S-образной функции (б) принадлежности для значений параметров а=3, b=6
Общая постановка задачи
Дано 3 нечетких множества в форме функций принадлежности. Необходимо построить функцию принадлежности заданного нечеткого множества D согласно Вашего варианта и определить степень принадлежности одного элемента множеству D, используя один из подходов. При этом необходимо рассчитать и построить графики:
