Предложенный американским специалистом в области исследования операций Томасом Саати метод аналитической иерархии (analytic hierarchy process; другой вариант русского перевода — метод анализа иерархий) оказался одним из наиболее востребованных методов принятия решений при многих критериях.
В основе методики лежат две идеи. Первая — это идея иерархической декомпозиции системы критериев. Вторая — идея перехода от непосредственной оценки важности отдельных критериев и качества альтернатив с точки зрения критериев к сравнительной попарной оценке критериев и альтернатив. Рассмотрим их на примере простейшей иерархии (рис. 4.1).
| Глобальная цель |
| Локальная цель 1 |
| Локальная цель 2 |
| Критерий 1 |
| Критерий 2 |
| Критерий 3 |
| Критерий 4 |
| Критерий 5 |
| Критерий 6 |
| А 1 |
| А 2 |
| А 3 |
| А 1 |
| А 2 |
| А 3 |
| А 1 |
| А 2 |
| А 3 |
| А 1 |
| А 2 |
| А 3 |
| А 1 |
| А 2 |
| А 3 |
| А 1 |
| А 2 |
| А 3 |
Рис. 4.1. Пример иерархии, (А – альтернатива 1,2….).
Смысл идеи иерархии здесь состоит в следующем. Выделены одна глобальная, две локальные цели и по три критерия, выражающие степень реализации каждой из локальных целей. Обе локальные цели оцениваются с точки зрения глобальной цели (в какой мере каждая из них важна для реализации последней). Все критерии оцениваются с точки зрения соответствующей локальной цели (в какой мере они ее отражают). Затем каждая из трех альтернатив оценивается с точки зрения каждого из критериев (в какой мере она ему соответствует). Таким образом, у нас должно быть в данном случае 18 оценок альтернатив, плюс 6 оценок значимости критериев, плюс 2 оценки важности локальных целей. После того, как все оценки получены, «снизу вверх» начинается расчет. Веса критериев вычисляются путем умножения значимости критерия на важность локальной цели, на которую «работает» данный критерий. Интегральные оценки альтернатив находятся по следующей схеме: оценка альтернативы по каждому критерию умножается на вес критерия, и все оценки данной альтернативы складываются. Поскольку оценки всех элементов иерархии на каждом ее уровне нормируются (т.е. в сумме дают единицу), то и интегральные оценки альтернатив тоже в сумме будут давать единицу. Выбирается альтернатива, имеющая максимальную интегральную оценку.
Идея попарного сравнения работает так. Каждая из необходимых нам в рассматриваемом примере 26 оценок получается в результате следующей процедуры. Элементы иерархии одного уровня, связанные с одним вышестоящим узлом, сравниваются попарно между собой. Результаты сравнения заносятся в квадратную таблицу (матрицу) размера n*n, где п — число элементов иерархии на данном уровне. Поскольку в каждой паре сравнение достаточно произвести только один раз (если в результате сравнения первой локальной цели со второй выяснилось, что первая локальная цель важнее, нет необходимости сравнивать вторую с первой) и результат сравнения любого элемента иерархии с ним же самим очевиден, то всего на каждом уровне иерархии придется провести п(п - 1)/2 сравнений. В нашем примере лицу, принимающему решение, пришлось бы осуществить 25 попарных сравнений (нужно 1 сравнение для локальных целей; по 3 — для критериев, соответствующих каждой из двух локальных целей – всего 6; по 3 — для альтернатив по каждому из шести критериев – всего 18). При проведении сравнений используется числовая шкала, представленная в табл. 4.4.
Табл.4.4. Шкала попарных сравнений в методе аналитической иерархии
| Позиция шкалы | Описание позиции |
| Равная важность для целей и критериев. Равное качество для альтернатив. (Пример: две локальные цели вносят одинаковый вклад в достижение глобальной цели). | |
| Умеренное превосходство первого из двух сравниваемых элементов иерархии над вторым. Имеются некоторые соображения в пользу предпочтения первого элемента, но недостаточно убедительные. | |
| Существенное превосходство первого из двух сравниваемых элементов иерархии над вторым. Имеются надежные суждения или логические выводы для предпочтительности первого элемента. | |
| Значительное превосходство первого из двух сравниваемых элементов иерархии над вторым. Существуют убедительные свидетельства в пользу первого элемента. | |
| Очень большое превосходство первого из двух сравниваемых элементов иерархии над вторым. |
Обратите внимание, что в соответствии с идеями, рассмотренными ранее (материалы по шкалированию), мы можем утверждать, что получаемые таким способом оценки являются количественными. Если, по мнению эксперта, соотношение между сравниваемыми элементами иерархии носит промежуточный характер между указанными в табл. 4.4. вариантами, то используются четные оценки: 2, 4, 6, 8. Наконец, если первый элемент иерархии уступает второму, то результат сравнения будет представлен обратными величинами: 1/3, 1/5, 1/7, 1/9. Таким образом, элементы матриц, построенных по результатам попарных сравнений, симметричные относительно главной диагонали, будут обязательно взаимно обратными.
Из полученной матрицы оценок элементов иерархии данного уровня рассчитываются элементы ее собственного вектора, соответствующего максимальному собственному значению. Логика, в соответствии с которой в качестве весов берутся именно эти параметры, такова. Пусть w1,..., wn — оценки элементов иерархии (веса критериев), оцененные по шкале от 1 (самый неважный) до 9 (самый важный). Тогда матрица попарных сравнений критериев при условии идеально логичного поведения ЛПР должна была бы выглядеть так:

C точки зрения математика, это — очень специфическая матрица. Все ее строки пропорциональны друг другу. Каким образом из этой матрицы можно получить сами веса w1,..., wn? Нетрудно видеть, что для этого нужно матрицу A умножить на вектор w = (w1,..., wn). Имеем
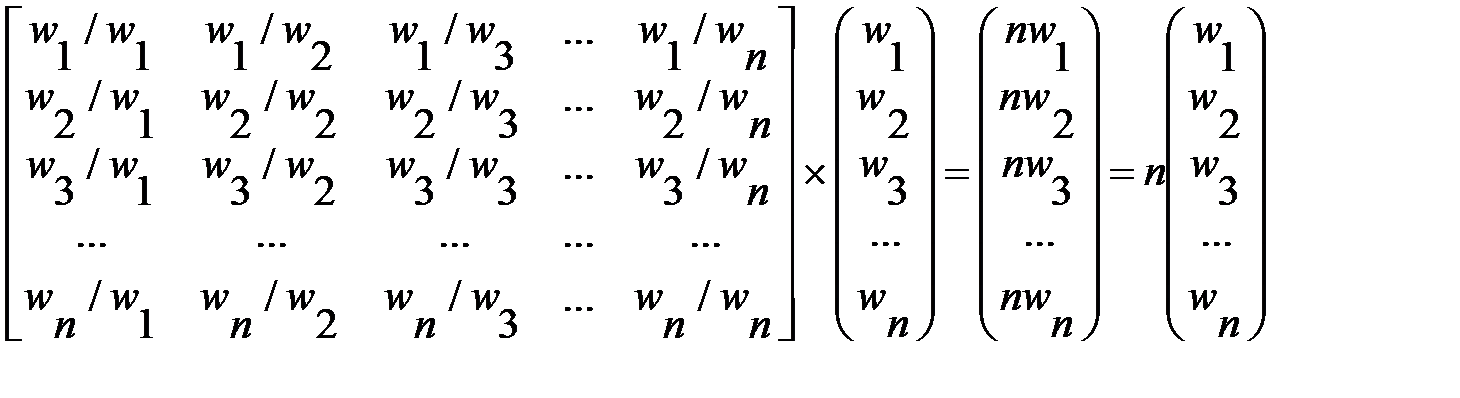
Это уравнение можно переписать в виде
А × w = n w. (4.1)
С математической точки зрения это означает, что вектор весов w есть собственный вектор матрицы A, соответствующий собственному значению п. Структура матрицы A такова, что ее максимальное собственное значение равно n, а все остальные значения равны нулю. Компоненты вектора w могут быть вычислены с помощью простых формул:
 (4.2)
(4.2)
 (4.3)
(4.3)
Заметим, что уравнение (4.2) — это не что иное, как формула вычисления так называемого среднего геометрического — стандартная операция, которая входит в библиотеку встроенных функций Microsoft Excel. Поэтому реализация метода аналитической иерархии каких-либо специфических вычислительных сложностей не таит.
Однако все это справедливо лишь при условии, что лицо, принимающее решение, действует абсолютно логично. На практике это, разумеется, не так, в результате чего матрица A приобретает несколько иной вид и свойства. Речь идет о следующем. Предположим, ЛПР утверждает, что критерий 1 значительно превосходит по важности критерий 2, а критерий 2 равен по важности критерию 3. Каков должен быть результат сравнения по важности критерия 1 и критерия 3? Вопреки, казалось бы очевидному, на практике часто оказывается, что ЛПР утверждает, что критерий 1 лишь умеренно превосходит по важности критерий 3. Дело тут не в неразумности ЛПР, а в том, что в процессе попарных сравнений ему не удается держать в памяти все свои предыдущие ответы и в ходе опроса он постоянно корректирует, переоценивает свои предыдущие суждения. Поэтому максимальное собственное значение λmax матрицы A оказывается несколько большим п, а это и является индикатором нарушения логики в ответах ЛПР. Следует отметить, что трудность, с которой мы здесь сталкиваемся, является оборотной стороной эффективного принципа декомпозиции: сложную задачу непосредственной оценки критериев и альтернатив мы заменили множеством относительно простых задач их сравнительной (попарной) оценки. При «обратной сборке» полученных ответов на частные простые вопросы и возникает та самая трудность.
Нахождение собственных векторов и собственных значений— это классическая задача вычислительной математики, эффективные методы решения которой хорошо известны. Для матрицы рассчитывается ее фактическое максимальное собственное значение λmax и так называемый индекс однородности ИО (т.е. непротиворечивости) суждений ЛПР:
ИО = (λmax – n)/(n-1)
Найденное значение индекса однородности сопоставляется со средним его значением для матриц данного размера. Эти средние значения получены в результате компьютерного моделирования произвольных (совершенно не ограниченных логикой) ответов ЛПР на вопросы о попарном сравнении элементов. Если индекс однородности составляет не более 10% от среднего значения индекса, то результаты попарных сравнений считают приемлемыми. В противном случае ЛПР предлагают пересмотреть свои ответы.
Процесс отыскания собственных векторов не должен быть пугающе сложным для ЛПР. Для него вся эта процедура, составляющая внутреннюю механику метода аналитической иерархии, невидима.
Помимо изящных идей иерархической декомпозиции задачи принятия решения и перехода от непосредственной оценки к попарному сравнению, успеху метода аналитической иерархии в очень большой степени способствовала компьютерная реализация методики — программа Expert Choice. Благодаря дружественному интерфейсу и предоставляемым возможностям групповой работы и обмена данными со стандартными приложениями Microsoft Office программа Expert Choice получила широкое распространение. В частности, она использовалась в таких компаниях, как ABN Amro, Allianz Life, America Online, Ford Motor Company, General Electric, General Motors, Hewlett Packard, IBM, John Hancock, Lockheed Martin, Mayo Collaborative Services, а также National Association of Counties, National Association of Home Builders.
Так называемая пробная версия программы Expert Choice может быть загружена с сайта производящей ее компании, созданной Т. Саати с сотрудниками: www. expertchoice.com/software/grouptrialreg.htm.
Типичные области применения данной методики — это распределение ресурсов; наем, оценка и продвижение персонала; оценка слияний и поглощений; управление качеством; реструктуризация; реинжиниринг бизнес-процессов; оценка инвестиций; стратегическое планирование.
Пример (распределение энергии).
Предположим, что нам необходимо разрешить проблему распределения энергии в некоторой развитой стране между тремя ее крупнейшими пользователями: бытовым потреблением (БП), транспортом (TP) и промышленностью (ПР). Они составляют третий, или низший, уровень иерархии. Целями, по отношению к которым оцениваются эти потребители, являются вклад в развитие экономики (Э), вклад в качество окружающей среды (С) и вклад в национальную безопасность (Б). Цели составляют второй уровень иерархии. Общая цель — благоприятное социальное и политическое положение (Бл) — первый уровень иерархии (рис. 2).



Необходимые пояснения к таблице. Экономика имеет сильное превосходство перед окружающей средой (5) и слабое перед национальной безопасностью (3). Числа во 2-й и 3-й строках выбраны так, чтобы полученная матрица сравнений была обратно-симметричной и согласованной. Столбец приоритетов, вычисленный любым из описанных выше четырех способов, имеет вид
 (4.4)
(4.4)
Следовательно, в соответствии со сравнением по социально-политическому влиянию экономика получает приоритет 0,65, окружающая среда — 0,13 и национальная безопасность — 0,22 (рис. 3).

Проведем теперь оценку относительной важности каждого потребителя с точки зрения экономики, окружающей среды и национальной безопасности (составляющих второй уровень иерархии).
Соответствующие матрицы попарных сравнений, индексы согласованности и столбцы приоритетов имеют следующий вид:



Запишем полученные столбцы в виде матрицы. Имеем:
 (4.5)
(4.5)
Умножая эту матрицу на столбец w (4.4), находим искомый столбец приоритетов третьего уровня иерархии, представляющего потребителей энергии БП, TP и ПР (взвешенный согласно их общему влиянию):
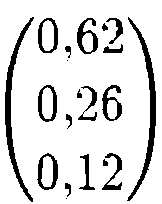
Итак, в соответствии с нашими вычислениями на бытовое потребление следует выделить 62% энергии, на транспорт — 26% и на промышленность — 12%.