Представим систему линейных уравнений для рассмотренного примера реализации МНК для параболической аппроксимирующей функции:
Представим данную систему уравнений в матричной форме. Правая часть системы уравнений представляет собой матрицу столбец В.
Матрица А формируется коэффициентами, которые определяются в зависимости от вида после получения производной и подстановкой из имеющейся выборки данных.
Матрица столбец R (root) представляет собой неизвестные переменные, которые необходимо рассчитать.
Таким образом, получено матричное представление системы уравнений:
Функции и операции над матрицами, используемые для получения решения :
1. Функция inv(Y) - вычисляет матрицу, обратную квадратной матрице Y.
2. «'» — транспонирование матрицы, то есть замена строк столбцами и наоборот. Например, Y' — транспонированная матрица Y.
3. «^» — возведение матрицы в степень. Y^р — это Y в степени р, если р — скаляр. Если р — целое число, то степень матрицы вычисляется путем умножения Y на себя р раз. Если р — целое отрицательное число, то Y сначала инвертируется.
4. «\» — левое деление. Выражение 
дает решение ряда систем линейных уравнений , где А — матрица размера 
и В — матрица столбец.
5. «/» — правое деление. Выражение 
дает решение ряда систем линейных уравнений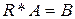 
.
На основании описанных функций и операций, возможны следующие подходы к решению системы уравнений :
1. С использованием операции левого деления:
>> A=[2,3,-1; 1,-2,1; 1,0,2]
B=[9; 3; 2]
R=A\B
A =
2 3 -1
1 -2 1
1 0 2
B =
9
3
2
R =
4
0
-1
2. Решение при помощи метода обратной матрицы.
>> R=inv(A)*B
R =
4.0000
-0.0000
-1.0000
Пример. Реализация МНК в среде MatLab. Реализуем аппроксимацию параболической зависимости 
.
% исходные данные
X = [0.2, 0.4, 0.6, 0.8, 1, 1.2, 1.4, 1.6, 1.8, 2, 2.2, 2.4];
Y = [0.07, 0.47, 0.66, 1.33, 1.94, 2.93, 3.87, 5.17, 6.42, 8.05, 9.63, 11.57];
A=zeros(3,3); % Матрица, содержащая суммы столбцов исходных данных по Х
B=zeros(3,1); % Матрица, содержащая суммы столбцов исходных данных по Y
%Формирование матриц A и B
for i=1:1:12
A(1,1)=A(1,1)+(X(i)^4);
A(1,2)=A(1,2)+(X(i)^3);
A(1,3)=A(1,3)+(X(i)^2);
A(2,1)=A(2,1)+(X(i)^3);
A(2,2)=A(2,2)+(X(i)^2);
A(2,3)=A(2,3)+X(i);
A(3,1)=A(3,1)+(X(i)^2);
A(3,2)=A(3,2)+X(i);
A(3,3)=A(3,3)+i;
B(1)=B(1)+(X(i)^2)*Y(i);
B(2)=B(2)+X(i)*Y(i);
B(3)=B(3)+Y(i);
end;
%>> A
%A =
% 97.1360 48.6720 26.0000
% 48.6720 26.0000 15.6000
% 26.0000 15.6000 78.0000
%>> B
%BS =
% 194.3996
% 97.4180
% 52.1100
%Сформирована система уравнений, которую можно решить любым удобным методом (например, метод обратной матрицы).
Root=zeros(1,3);% массив для записи корней уравнения
Root=inv(A)*B
%Root =
% 1.9987
% 0.0048
% 0.0009
% Вычисление СКО
E=0;
for i=1:1:12
F(i)=Root(1)*X(i)^2+Root(2)*X(i)+Root(3);
E=E+(Y(i)-F(i))^2;
end;
S=sqrt(E/12);
%>>S
%S =
% 0.0649
% Вывод графиков
plot(X,Y,'r.'); % исходная функция
hold on;
plot(X,F,'k'); % аппроксимированная функция
На рис. 4.3 представлен результат аппроксимации. Красные точки принадлежат исходной функции, а кривая соответствует аппроксимирующей функции.
Рис. 4.3. Графики исходной и аппроксимированной функций
Пример. Формирование выборки с учетом вида аппроксимирующей функции и погрешности отклонения данных с целью придания случайного характера распределения значений выборки.
% формирование выборки на основании эмпирической формулы с заданным случайным отклонением для нахождения аппроксимирующей функции
n=20;
a=5; % коэффициент аппроксимирующей функции
b=5; % коэффициент аппроксимирующей функции
c=5; % коэффициент аппроксимирующей функции
h=1:n; % аргумент эмпирической формулы
p=1; %погрешность +/- отклонение от функции y
for i=1:n
f(i)=a/h(i)+b; % эмпирическая формула
% y с погрешностью
maxY(i)=f(i)+p;
minY(i)=f(i)-p;
dY(i)=maxY(i)-minY(i);
y(i)=dY(i)*rand+minY(i);
% округление y до сотых
y(i)=y(i)*100;
y(i)=round(y(i))/100;
% x с погрешностью
maxX(i)=x(i)+p;
minX(i)=x(i)-p;
dX(i)=maxX(i)-minX(i);
x(i)=dX(i)*rand+minX(i);
% округление x до сотых
x(i)=x(i)*100;
x(i)=round(x(i))/100;
end;
plot(h,f, x,y,'*');
XX=x';
YY=y';
Выполнение работы
Необходимо подобрать аппроксимирующую функцию с наименьшим квадратическим отклонение, выражающую функциональную зависимость между X и Y.
| Вар. 1 | Вар. 2 | Вар. 3 | Вар. 4 | Вар. 5 | ||||||
| X | Y | X | Y | X | Y | X | Y | X | Y | |
| 0,79 | 9,51 | 1,70 | 0,96 | 1,97 | 10,83 | 0,54 | 0,57 | 0,400 | 9,99 | |
| 2,54 | 6,97 | 1,93 | -0,90 | 1,54 | 7,51 | 1,64 | -0,54 | 1,39 | 8,04 | |
| 3,6 | 6,10 | 3,26 | -0,35 | 3,02 | 5,87 | 3,64 | 0,69 | 3,46 | 6,58 | |
| 3,37 | 6,11 | 4,16 | -0,53 | 4,53 | 6,42 | 4,14 | 0,21 | 4,16 | 6,10 | |
| 5,33 | 5,78 | 5,20 | 0,240 | 5,32 | 5,17 | 5,4 | -0,30 | 5,54 | 6,45 | |
| 6,06 | 6,25 | 5,07 | -0,03 | 5,34 | 5,87 | 5,88 | 0,81 | 5,57 | 6,44 | |
| 7,55 | 5,97 | 6,82 | 0,20 | 7,18 | 6,59 | 6,93 | 0,24 | 7,56 | 5,38 | |
| 7,73 | 7,92 | -0,46 | 8,88 | 5,51 | 8,35 | 0,070 | 8,01 | 5,76 | ||
| 8,57 | 4,92 | 9,10 | 0,49 | 8,90 | 5,87 | 9,82 | 1,54 | 9,45 | 5,71 | |
| 10,31 | 5,81 | 10,4 | 1,61 | 10,07 | 6,18 | 9,52 | 1,49 | 9,58 | 5,54 | |
| 11,12 | 5,98 | 10,1 | 2,35 | 11,36 | 5,56 | 10,26 | 1,71 | 10,9 | 5,39 | |
| 12,59 | 4,82 | 11,92 | 1,93 | 11,48 | 5,15 | 11,38 | 0,98 | 12,17 | 6,07 | |
| 12,7 | 5,81 | 13,58 | 4,63 | 13,73 | 5,54 | 13,17 | 1,49 | 13,31 | 5,66 | |
| 14,68 | 5,42 | 13,67 | 5,28 | 13,23 | 5,17 | 14,64 | 1,89 | 14,02 | 5,14 | |
| 15,47 | 5,64 | 15,48 | 6,71 | 14,6 | 5,22 | 15,85 | 3,82 | 14,52 | 5,41 | |
| 15,96 | 5,22 | 15,4 | 10,5 | 16,67 | 5,12 | 16,31 | 4,08 | 16,27 | 5,40 | |
| 16,68 | 5,38 | 16,34 | 14,05 | 16,78 | 5,10 | 17,08 | 5,69 | 17,47 | 5,19 | |
| 18,01 | 5,63 | 17,74 | 19,4 | 17,28 | 18,95 | 5,4 | 17,8 | 5,60 | ||
| 18,73 | 5,47 | 18,03 | 25,64 | 18,17 | 4,78 | 18,65 | 5,93 | 18,84 | 5,20 | |
| 19,97 | 4,74 | 20,25 | 32,66 | 19,51 | 5,11 | 19,73 | 8,95 | 20,33 | 5,64 |
| Вар. 6 | Вар. 7 | Вар. 8 | Вар. 9 | Вар. 10 | ||||||
| X | Y | X | Y | X | Y | X | Y | X | Y | |
| 1,76 | 0,33 | 0,58 | 3,59 | 1,43 | 3,93 | 0,54 | 2,19 | 0,26 | 0,28 | |
| 2,75 | 0,42 | 1,74 | 2,28 | 1,51 | 3,30 | 1,86 | 1,37 | 2,30 | -0,09 | |
| 2,28 | 0,07 | 3,48 | 1,78 | 3,11 | 3,09 | 3,49 | 1,37 | 2,62 | 0,66 | |
| 4,43 | -0,68 | 4,25 | 1,69 | 3,77 | 2,42 | 4,26 | 0,70 | 4,77 | -0,18 | |
| 5,34 | -0,14 | 4,67 | 1,75 | 4,98 | 1,93 | 4,97 | 1,21 | 4,48 | 0,42 | |
| 6,06 | 0,64 | 5,61 | 1,64 | 5,55 | 1,69 | 6,31 | 0,37 | 5,58 | 0,54 | |
| 7,01 | 0,88 | 7,23 | 1,34 | 6,76 | 1,45 | 6,62 | 0,60 | 6,01 | -0,42 | |
| 0,58 | 7,63 | 1,21 | 8,11 | 1,34 | 8,14 | 0,93 | 7,87 | -0,21 | ||
| 8,78 | 1,69 | 9,01 | 0,85 | 9,31 | 1,84 | 9,41 | 0,09 | 8,58 | -0,34 | |
| 9,48 | 0,34 | 10,36 | 0,86 | 10,21 | 1,71 | 9,54 | -0,01 | 10,87 | -0,45 | |
| 11,68 | 1,86 | 11,31 | 0,94 | 11,28 | 1,68 | 11,19 | 0,90 | 10,79 | 0,81 | |
| 11,43 | 2,95 | 12,46 | 0,74 | 12,49 | 0,94 | 0,26 | 12,13 | 0,08 | ||
| 13,17 | 3,24 | 13,04 | 0,23 | 13,15 | 0,76 | 12,55 | 0,62 | 12,54 | 0,15 | |
| 14,02 | 3,47 | 13,98 | 0,40 | 13,74 | 0,81 | 14,2 | 0,56 | 13,37 | 1,21 | |
| 15,3 | 4,94 | 14,71 | 0,77 | 14,7 | 0,88 | 15,08 | 0,27 | 14,07 | 1,04 | |
| 15,6 | 7,17 | 15,83 | 0,66 | 16,45 | 15,67 | 0,13 | 16,5 | 0,09 | ||
| 17,65 | 8,20 | 16,63 | 0,90 | 17,08 | 0,84 | 17,42 | 0,18 | 16,34 | 0,87 | |
| 18,55 | 11,96 | 18,46 | 0,10 | 18,21 | 1,01 | 17,86 | -0,01 | 18,09 | 1,70 | |
| 18,22 | 15,8 | 18,65 | 0,13 | 19,36 | 0,76 | 18,58 | 0,07 | 19,16 | 0,59 | |
| 20,75 | 19,59 | 0,11 | 20,25 | 1,25 | 20,33 | 0,25 | 20,79 | 2,31 |
Контрольные вопросы к защите
1. Объясните цель метода наименьших квадратов?
2. Что такое аппроксимирующая функция?
3. Каким образом выбирается вид аппроксимирующей функции?
4. Какие виды аппроксимирующих функций вы знаете?
5. Что представляет собой мера отклонения?
6. Каким образом подбираются критерии аппроксимации?
7. Опишите процесс получения аппроксимирующей функции при линейной зависимости?
8. Опишите процесс получения аппроксимирующей функции при квазилинейной зависимости?
9. Что представляет собой среднеквадратичное отклонение?
10. Почему ошибка отклонения i-й итерации возводится в квадрат?