ЦЕЛЬ РАБОТЫ
1. Ознакомится с методикой обработки и представлением результатов прямых многократных равноточных измерений с учетом требований ГОСТ 8.207-76 ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения.
2. Получение навыков практического использования таблиц ГОСТ 8.207-76 ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения.
ЗАДАНИЕ
1. Статистическая обработка результатов измерений.
2. Исключение аномальных результатов наблюдений.
3. Определение статистических характеристик выборки.
4. Определение абсолютных погрешностей.
5. Интервальная оценка параметров распределения.
НЕОБХОДИМЫЕ ПРИБОРЫИ ПОСОБИЯ
ГОСТ 8.207-76 ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Равноточными называются измерения, у которых все значения отсчетов 
имеют одинаковую дисперсию (точность).
Обработка результатов многократных равноточных измерений производится в следующем порядке:
1. Определение оценок числовых характеристик 
и 
закона распределения вероятности результата измерения ( и – среднее арифметическое и оценка среднего квадратического отклонения измеряемой величины соответственно);
5. Исключение «грубых промахов», если таковые имеются, из результатов измерений и пересчет оценок числовых характеристик закона распределения вероятности результата измерения;
6. Представление результата измерения в виде доверительного интервала, соответствующего определенному уровню доверительной вероятности
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. При многократном измерении силы получены значения: 263,5; 268,1; 273,9; 265,4; 267,7; 261,5; 266,7; 264,4; 267,2; 271,7; 270,3; 272,9, 280,1; 265,3(Н). Погрешность динамометра составила +0,6 Н. Укажите доверительные границы истинного значения силы с вероятностью Р = 0,9; Р = 0,95; Р = 0,99
2. Исключаем известную систематическую погрешность (
) из результатов измерения (поправку равна: 
). Результаты измерений после исключения систематической погрешности: 262,9; 267,5; 273,3; 264,8; 267,1; 260,9; 266,1; 263,8; 266,6; 271,1; 269,7; 272,3; 279,5; 264,7.
3. Проверяем результаты наблюдений на наличие грубых промахов:
3.1. Располагаем результаты наблюдений по возрастанию
260,9<262,9<263,8<264,7<264,8<266,1<266,6<267,1<267,5<269,7<271,1<272,3<273,3<279,5
Определяем размах результатов измерений:
.
3.2. Определяем среднее арифметическое значение результатов измерений:
.
3.3. Определяем среднюю квадратическую погрешность результатов единичных измерений:
.
3.4. Проведем проверку наличия грубых погрешностей в представленной выборке.
Рассчитаем значение критерия Романовского:
;
;
.
;
;
;
;
Сравниваем полученные значения с критерием 
для 
. Проверяем выполнение условия 
, т.к. для всех 
условие не выполняется, то среди результатов измерений промахов не обнаружено.
4. Определяем абсолютные случайные погрешности 
исправленных отдельных результатов наблюдений 
:
.
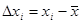Проверяем условие 
.
Результаты заносим в таблицу:
5. Определяем среднее квадратическое отклонение измеренного напряжения (п.5.4, ф.4 ГОСТ Р 8.736-2011):
.
6. Определяем доверительные границы случайной погрешности (п.6.1, ф.5 ГОСТ Р 8.736-2011):
,
где 
- коэффициент Стьюдента, который в зависимости от доверительной вероятности и числа результатов измерений. 
; 
; 
(Приложение Б).
для 
;
для 
;
для 
.
7. Запишем результаты измерения:
; ;
; ;
; .
Или
; ;
; ;
; .
Полученные данные заносим в табл.2.
8. Начертим график распределения результатов измерений в зависимости от вероятности получения доверительного интервала.
Рисунок 1 – График распределения результатов измерений
ВЫВОД
В ходе выполнения работ изучены особенности обработки равноточных прямых измерений в соответствии с ГОСТ 8.207-76 ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения. Проведены расчеты среднего арифметического 14-ти результатов измерения силы, проведена проверка наличия грубых промахов по критерию Романовского, промахи не выявлены. Определены среднее квадратическое отклонение единичного результата измерения и серии. В заключительной части определены доверительные интервалы абсолютной погрешности для различных значений доверительной вероятности.