Формула Кардано
Если воспользоваться современным математическим языком и современной символикой, то вывод формулы Кардано может быть найден с помощью следующих в высшей степени элементарных соображений:
Пусть нам дано общее уравнение 3-й степени:
ax3+3bx2+3cx+d=0 (1)
Если положить
, то мы приведем уравнение (1) к виду
(2)
где 
,
.
Введем новое неизвестное U с помощью равенства
.
Внося это выражение в (2), получим
(3)
Отсюда
,
следовательно
Если числитель и знаменатель второго слагаемого умножить на выражение 
и учесть, получающееся в результате выражение для u оказывается симметричным относительно знаков «+» и «-», то окончательно получим
.
(Произведение кубических радикалов в последнем равенстве должно равняться p).
Это и есть знаменитая формула Кардано. Если перейти от y вновь к x, то получим формулу, определяющую корень общего уравнения 3-й степени.
Молодой человек, так безжалостно обошедшийся с Тарталья, разбирался в математике столь же легко, как и в правах неприхотливой тайны. Феррари находит способ решения уравнения 4-й степени. Кардано поместил этот способ в свою книгу. Что же представляет собой этот способ?
Пусть 
(1)
– общее уравнение 4-й степени.
Если положить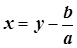 
,
то уравнение (1) можно привести к виду
, (2)
где p,q,r – некоторые коэффициенты, зависящие от a,b,c,d,e. Легко видеть, что это уравнение можно записать в таком виде:
(3)
В самом деле, достаточно раскрыть скобки, тогда все члены, содержащие t, взаимно уничтожается, и мы возвратимся к уравнению (2).
Выберем параметр t так,чтобы правая часть уравнения (3) была полным квадратом относительно y. Как известно, необходимым и достаточным условием этого является обращение в нуль дискриминанта из коэффициентов трехчлена (относительно y), стоящего справа:
(4)
Получили полное кубическое уравнение, которое мы уже можем решить. Найдем какой либо его корень и внесем его в уравнение (3), теперь примет вид
.
Отсюда
.
Это квадратное уравнение. Решая его, можно найти корень уравнения (2), а следовательно и (1).
За 4 месяца до смерти Кардано закончил свою автобиографию, которою он напряженно писал весь последний год и которая должна была подвести итог его сложной жизни. Он чувствовал приближение смерти. По некоторым сведениям его собственный гороскоп связывал его кончину с 75- летием. Он умер 21сентября 1576г. за 2 дня до годовщины. Имеется версия, что он покончил с собой в ожидании неминуемой смерти или даже чтобы подтвердить гороскоп. В любом случае Кардано – астролог относился к гороскопу серьезно.
Замечание о формуле Кардано
Проанализируем формулу для решения уравнения 
в вещественной области. Итак,
При вычислении x нам приходится извлекать в начале квадратный корень, а затем кубический. Мы сможем извлечь квадратный корень, оставаясь в вещественной области, если 
. Два значения квадратного корня, отличающихся знаком, фигурируют в разных слагаемых для x. Значения кубического корня в вещественной области единственно и получается единственный вещественный корень x при 
. Исследуя график кубического трехчлена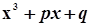 
,нетрудно убедиться, что он в самом деле имеет единственный вещественный корень при 
. При 
имеется три вещественных корня. При 
имеется двукратный вещественный корень и однократный, а при 
-трехкратный корень x=0.
Продолжим исследование формулы при 
. Оказывается. Что если при этом уравнение с целыми коэффициентами имеет целочисленный корень, при вычислении его по формуле могут возникнуть промежуточные иррациональности. Например, уравнение 
имеет единственный корень (вещественный) – x=1. Формула Кардано дает для этого единственного вещественного корня выражение
.
Значит,
. Но фактически любое доказательство предполагает использование того, что это выражение является корнем уравнения 
. Если же не угадать того, при преобразовании будут возникать неистребимые кубические радикалы.
О проблеме Кардано – Тартальи вскоре забыли. Формулу для решения кубического уравнения связали с «Великим искусством» и постепенно стали называть формулой Кардано.
У многих возникало желание восстановить истинную картину событий в ситуации, когда их участники несомненно не говорили всей правды. Для многих было важно установить степень вины Кардано. К концу XIX века часть дискуссий стала носить характер серьезных историко-математических исследований. Математики поняли, какую большую роль в конце XVI века сыграли работы Кардано. Стало ясно то, что еще раньше отмечал Лейбниц: «Кардано был великим человеком при всех его недостатках; без них он был бы совершенством».