Учебный модуль 7. Последовательности и ряды. Тема 17. Ряды Фурье. Основные определения. Разложение функций в тригонометрические ряды. Ряды от четных и нечетных функций. Интегральное преобразование Фурье.
ЛЕКЦИЯ 17. Ряды Фурье
Пусть функция f (x) определена на всей оси  и является периодической функцией с периодом 2 π. В этом случае достаточно рассмотреть поведение функции в интервале (−π, π ]. Тогда такую функцию можно представить в виде суммы функционального тригонометрического ряда, который называется рядом Фурье
и является периодической функцией с периодом 2 π. В этом случае достаточно рассмотреть поведение функции в интервале (−π, π ]. Тогда такую функцию можно представить в виде суммы функционального тригонометрического ряда, который называется рядом Фурье
 (17.1)
(17.1)
Числа 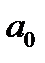 ,
,  ,….,
,….,  ,…,
,…,  ,…
,…  … называются коэффициентами ряда Фурье и вычисляются по формулам
… называются коэффициентами ряда Фурье и вычисляются по формулам

| (17.2) |

| (17.3) |

| (17.4) |
Коэффициент 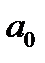 имеет смысл среднего значения функции f (x) на интервале (−π, π ].
имеет смысл среднего значения функции f (x) на интервале (−π, π ].
Замечание 1. Существует другой вариант записи ряда Фурье
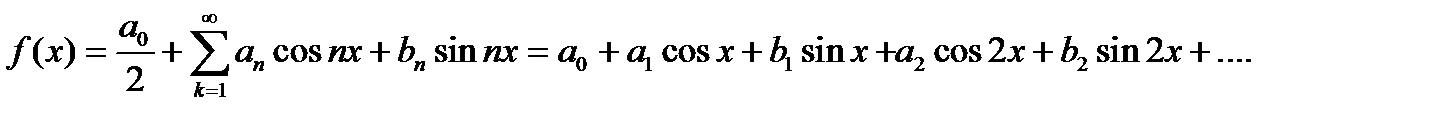
В этом случае  вычисляется по формуле
вычисляется по формуле

Эта формула совпадает с формулой (17.3) когда  .
.
Замечание 2. Для 2 π периодической функции можно рассматривать и интервал [ −π, π). Можно 2 π периодическую функцию, рассматривать на любом интервале длины 2 π. Если функция не является периодической, то она задается на интервале [ −π, π ].
Существует несколько разных ограничений на функцию f (x), обеспечивающих сходимость ряда Фурье к значению функции.
1. Если функция дифференцируема в точке  , тогда ряд Фурье сходится к значению функции в данной точке.
, тогда ряд Фурье сходится к значению функции в данной точке.
2. Функция называется кусочно монотонной на отрезке  , если отрезок можно разбить на конечное число интервалов
, если отрезок можно разбить на конечное число интервалов 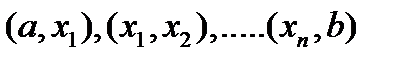 , таких что на каждом интервале функция или не убывает или не возрастает (рис. 17.1).
, таких что на каждом интервале функция или не убывает или не возрастает (рис. 17.1).
Если функция кусочно монотонна и ограничена на отрезке  , то она может иметь только точки разрыва первого рода.
, то она может иметь только точки разрыва первого рода.

Рис. 17.1. Кусочно монотонная функция на отрезке  , имеющая разрыв первого пода в точке
, имеющая разрыв первого пода в точке 
Ряд Фурье для кусочно монотонной, периодической с периодом 2 π, ограниченной на интервале [ −π, π ] функции f (x) сходится к значению функции во всех точках непрерывности. В точках с разрывов первого рода сходится к полусумме пределов функции слева и справа
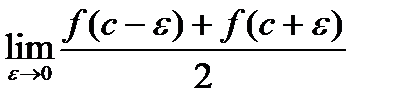 .
.
3. Пусть функция f (x) непрерывно в точке  и имеет в этой точке конечные односторонние пределы
и имеет в этой точке конечные односторонние пределы

 (17.5)
(17.5)
то в точке  ряд Фурье сходится к значению функции в данной точке.
ряд Фурье сходится к значению функции в данной точке.
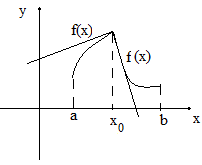
Рис. 17.2. Односторонние касательные.
Замечание. Существование пределов (17.5) означает наличие односторонних касательных слева и справа (или односторонних производных) (рис. 17.2).
При вычислении коэффициентов ряда Фурье полезны следующие формулы
 ,
,  ,
,
 (
( ).
).
Пример. Разложить периодическую функцию f (x) в ряд Фурье

Решение.

Найдем коэффициенты ряда Фурье.


Здесь мы объединили два интеграла от одной и той же функции. Первый интеграл равен нулю, второй вычислим методом интегрирования по частям. Напомним формулу метода интегрирования по частям в определенном интеграле
 ,
, 
Следовательно

Итого

Аналогично вычислим bn

Первый интеграл равен нулю (интеграл от нечетной функции по симметричному промежутку), второй вычислим методом интегрирования по частям

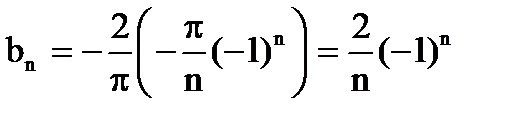 .
.
Итого 
Ряд Фурье для четных и нечетных функций.
Интеграл от нечетной функции по симметричному интервалу равен нулю,
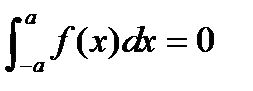 ,
,  нечетная, т. е.
нечетная, т. е. 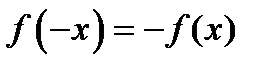 ,
,
а интеграл от четной функции по симметричному интервалу можно упростить «сдвоив» его
 ,
,  четная, т. е.
четная, т. е. 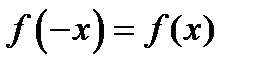
Если в ряд Фурье разлагается нечетная функция  , то произведение
, то произведение  есть также нечетная функция, а
есть также нечетная функция, а  - четная, следовательно,
- четная, следовательно,

| (17.5) |
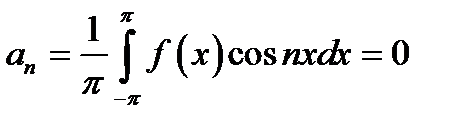
| (17.6) |

| (17.7) |
то есть, ряд Фурье для нечетной функции является разложением по синусам:

| (17.8) |
где

Если в ряд Фурье разлагается четная функция  , то произведение
, то произведение  есть также четная функция, а
есть также четная функция, а 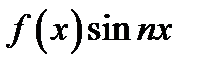 - нечетная, следовательно,
- нечетная, следовательно,

| (17.9) |
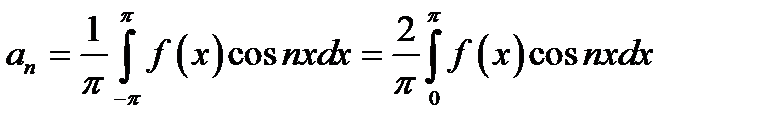
| (17.10) |

| (17.11) |
то есть, ряд Фурье четной функции является разложением только по косинусам:
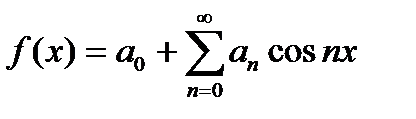
| (17.12) |
где


Пример.
Функция 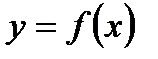 задана на промежутке
задана на промежутке  :
:

и продолжена четным образом на промежуток  , а затем продолжена
, а затем продолжена  -периодически, т.е. с периодом
-периодически, т.е. с периодом  . Сделать чертеж функции
. Сделать чертеж функции 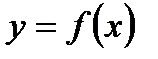 и найти ее разложение в ряд Фурье.
и найти ее разложение в ряд Фурье.
Сделаем чертеж четного продолжения функции 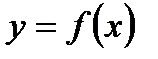 (рис. 17.3).
(рис. 17.3).

Определим коэффициенты  и
и 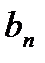 .
.

Рис. 17.3 Четное продолжение функции, заданной на интервале  .
.
Так как функция 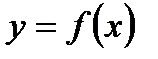 четным образом продолжена на промежуток
четным образом продолжена на промежуток  , то ряд Фурье является разложением только по косинусам
, то ряд Фурье является разложением только по косинусам
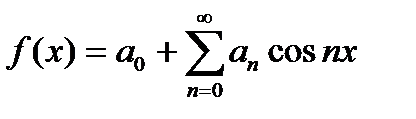 ,
,
а коэффициенты определяются по формулам (17.9, 17.10)


Здесь

 , так как
, так как 

так как 

так как  . Следовательно, подставив полученные выражения в формулу для
. Следовательно, подставив полученные выражения в формулу для 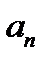 , получим
, получим
 =
=
Теперь мы можем написать разложение в ряд Фурье

Это выражение можно упростить, если учесть отдельно четные и нечетные значения n.
Для четных 


Для нечетных 

Ряд Фурье для функции с периодом  .
.
Для такой функцииряд Фурье имеет вид
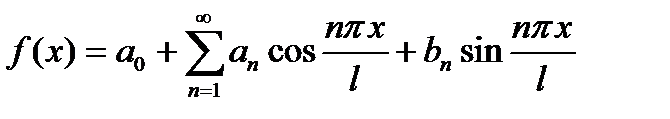 (17.13)
(17.13)

|

|

|
Это разложение можно получить из ряда Фурье, если ввести новую переменную  ,
,  ,
, 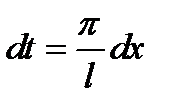
 ,
,  . Тогда, для переменной t можно написать стандартный ряд Фурье
. Тогда, для переменной t можно написать стандартный ряд Фурье
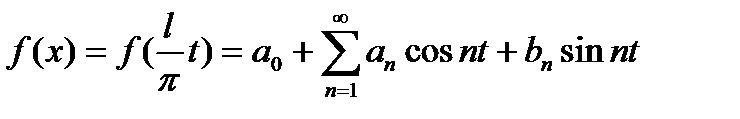

|

|

|
Вернемся к переменной  . Тогда
. Тогда

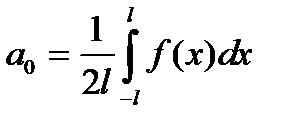
|

|
 . .
|
Все теоремы о сходимости ряда Фурье сохраняются и здесь. Существуют также возможность упростить вычисление для четных и нечетных функций.