НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Понятие первообразной
Основной задачей дифференциального исчисления является нахождение по заданной функции F (x) ее производной f (x). В интегральном исчислении основной задачей является обратная: нахождение функции F (x) по ее известной производной F ¢(x) = f (x). Искомую функцию F (x) называют первообразной функции f (x).
| Определение 1. Функцию F (x) называют первообразной функции f (x) на интервале (a, b), если " х Î (a, b) выполняется равенство F ¢(x) = f (x). |
Если F (x) является первообразной для функции f (x) на интервале (a, b), то и функция Ф (x) = F (x) + С, где С - произвольная постоянная, будет первообразной
для f (x) на (a, b). В самом деле, Ф ¢ (x) = (F (x) + С)¢ = F ¢ (x) = f (x) " х Î (a, b).
Т.о., если функция f (x) имеет на (a, b) первообразную, то она имеет на этом интервале бесконечное множество первообразных. Между двумя различными первообразными для одной и той же функции существует тесная связь, которая устанавливается следующей теоремой.
| Теорема 1. ЕслиF (x) иФ (x) – две любые первообразные для функции f (x) на интервале (a, b), то их разность равна некоторой постоянной Ф (x) – F (x) = С, С = const, х Î (a, b). |
· Пусть F (x) и Ф (x) – первообразные для функции f (x) на (a, b), т.е. F ¢ (x) = f (x) и Ф ¢ (x) = f (x) " х Î (a, b). Рассмотрим функцию j (x) = Ф (x) – F (x). Для нее имеем
j ¢ (x) = Ф ¢ (x) – F ¢ (x) = f (x) – f (x) = 0 " х Î (a, b).
Возьмем в интервале (a, b) любые две точки х 0 и х и применим теорему Лагранжа (о конечных приращениях) к функции j (x) на отрезке [ х 0, x ]. Тогда получим j (x) – j (x 0) = (x – x 0) j ¢(x), где x Î [ х 0, x ]. Т.к. j ¢ (x) = 0 на (a, b), то и j ¢(x) = 0 и, значит, j (x) = j (x 0) " х Î (a, b), т.е. функция j (x) на (a, b) постоянна. Т.о., Ф (x) – F (x) = С, где С = const, " х Î (a, b). ·
| Следствие. Если F (x) – одна из первообразных для функции f (x) на интервале (a, b), то любая другая первообразная Ф (x) для функции f (x) имеет вид Ф (x) = F (x) + С, где С - const. |
Неопределенный интеграл
| Определение. Совокупность всех первообразных для функции f (x), определенных на интервале (a, b), называется неопределенным интегралом от функции f (x) на этом интервале и обозначается символом ò f (x) dx. Здесь знак ò называетсязнаком интеграла, выражение f (x) dx – подынтегральным выражением, сама функция f (x) - подынтегральной функцией, аx называется переменной интегрирования. |
Если F (x) – какая-либо первообразная для функции f (x) на интервале (a, b), то в силу следствия будем иметь
| ò f (x) dx = F (x) + С, |
где С - произвольная постоянная.
Операция нахождения неопределенного интеграла называется интегрированием функции.
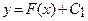
Геометрически неопределенный интеграл представляет
собой семейство “параллельных” кривых у = F (x) + С
(каждому числовому значению С соответствует опре-
деленная кривая семейства) (см. рис.). График каждой
первообразной (кривой) называется интегральной
кривой.
Условие существования неопределенного интеграла Рис.
| Теорема 2. Функцияf (x), непрерывная на интервале (a, b), имеет на этом интервале первообразную, а следовательно, и неопределенный интеграл. |
Свойства неопределенного интеграла
Будем считать, что все рассматриваемые функции определены и непрерывны на одном и том же интервале (a, b), следовательно, на этом интервале существуют неопределенные интегралы от этих функций.
1. Дифференциал от неопределенного интеграла равен подынтегральному выражению
| d (ò f (x) dx) = f (x) dx |
· d (ò f (х) dx) = d (F (x) + С) = d F (x) = F ¢(x) dx = f (x) dx. ·
2. Производная от неопределенного интеграла равна подынтегральной функции
| (ò f (x) dx)¢ = f (x) |
· Следует из свойства 1. ·
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс const
| ò d F (x) = F (x) + C |
· ò d F (x) = ò F ¢ (x) dx = ò f (х) dx = F (x) + С. ·
4. Постоянный множитель можно выносить за знак неопределенного интеграла или вносить под знак интеграла
| ò А f (х) dx = А ò f (х) dx |
· В силу свойства 2 имеем
(ò А f (x) dx)¢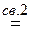 
А f (x), (А ò f (x) dx)¢ = А (ò f (x) dx)¢ 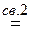А f (x).
Т. о., ò А f (x) dx и А ò f (x) dx являются первообразными для одной и той же функции А f (x). Следовательно, они отличаются друг от друга на некоторую постоянную С. ·
5. Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме неопределенных интегралов от этих функций
| ò(f (x) ± g (x)) dx = ò f (x) dx ± ò g (x) dx |
· В силу свойства 2 (ò(f (x) ± g (x)) dx)¢ 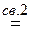f (x) ± g (x).
C другой стороны, (ò f (x) dx ± ò g (x) dx)¢ = (ò f (x) dx)¢ ± (ò g (x) dx)¢ 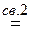f (x) ± g (x).
Таким образом, ò(f (x) ± g (x)) dx и ò f (x) dx ± ò g (x) dx являются первообразными для одной и той же функции f (x) ± g (x). Следовательно, они отличаются друг от друга на некоторую постоянную С. ·
неопределенный интеграл от линейной комбинации конечного числа функций равен линейной комбинации неопределенных интегралов от этих функций
6. (Инвариантность формулы интегрирования) Если ò f (x) dx = F (x) + С, то и
ò f (u) du = F (u) + С, где u = g (x) – произвольная функция, имеющая непрерывную производную.
· Пусть ò f (x) dx = F (x) + С и u = g (x). Рассмотрим сложную функцию F (u) = F (g (x)). В силу инвариантности формы первого дифференциала имеем d F (u) = F ¢(u) du = f (u) du. Отсюда ò f (u) du =ò d F (u) = F (u) + С. ·
Т.о., формула для неопределенного интеграла остается справедливой независимо от того, является ли переменная интегрирования независимой переменной или любой функцией от нее, имеющей непрерывную производную.
Например, ò cos (x) dx =sin (x) + С, следовательно,ò cos (x 2) d x 2=sin (x 2) + С,
ò cos (ln x) d (ln x)=sin (ln x) + С, ò cos (x +2) d (x +2)=sin (x +2) + С и т.д.
Табличные интегралы
Иногда к этому списку добавляют еще несколько интегралов:
Справедливость всех приведенных выше формул устанавливается с помощью дифференцирования, которое показывает, что производная правой части этих равенств равна подынтегральной функции.
Замечание. В силу инвариантности формулы интегрирования во всех интегралах (в т.ч. и табличных) х можно заменить на u (x), где u (x) – произвольная функция, имеющая непрерывную производную.