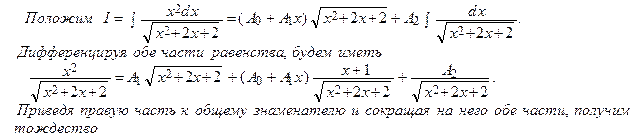Как было сказано выше, любую неправильную рациональную дробь можно представить в виде суммы некоторого многочлена и правильной рациональной дроби, причем это представление единственно. Интегрирование многочлена не представляет трудностей, поэтому рассмотрим вопрос об интегрировании правильной рациональной дроби.
Т.к. любая правильная рациональная дробь представима в виде суммы простейших дробей, то ее интегрирование сводится к интегрированию простейших дробей.
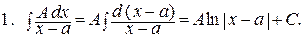
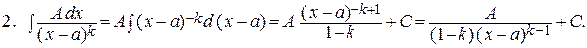
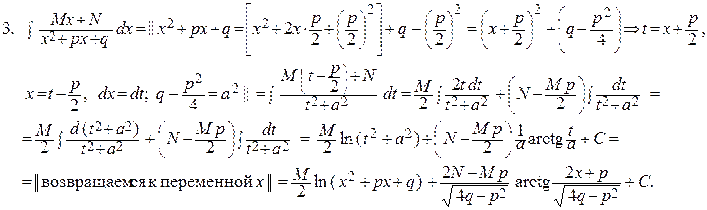
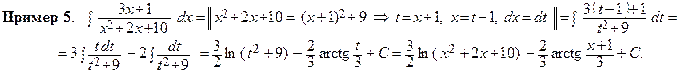
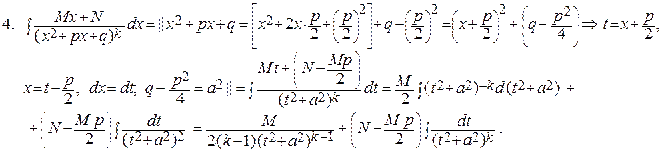
Интеграл в правой части обозначим через Jk и преобразуем его следующим образом:
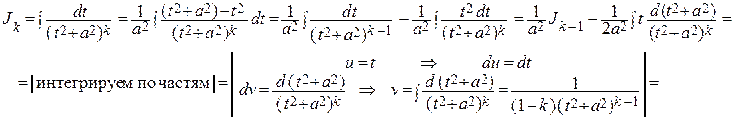
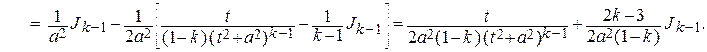
Т.о., мы получили рекуррентную формулу Jk = 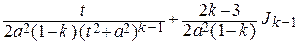 ,
,
которая позволяет найти интеграл Jk для любого k = 2, 3, ….
Действительно, интеграл J 1 является табличным: J 1 = 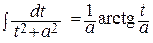 + С.
+ С.
Полагая в рекуррентной формуле k = 2, найдем:
J 2 = 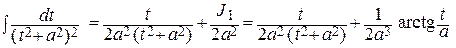 + С.
+ С.
Зная J 2 и полагая k = 3, легко найдем J 3 и т.д.
В окончательном результате, подставляя всюду вместо t и a их выражения через х и коэффициенты p и q, получим для первоначального интеграла выражение его через х и заданные числа M, N, p, q.
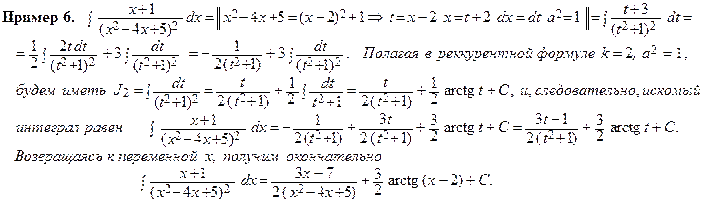
Интегрирование рациональных дробей (общий случай)
Из результатов пп.1 и 2 этого параграфа непосредственно следует
правило интегрирования рациональных дробей.
1. Если дробь неправильная, то представить ее в виде суммы многочлена и правильной дроби (см. п.2).
2. Разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших рациональных дробей.
3. Проинтегрировать многочлен и полученную сумму простейших дробей.

Разложим правильную дробь на простейшие дроби:
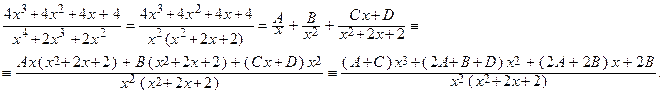
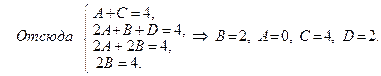
Т.о., 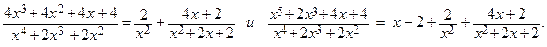
Интегрируем полученное равенство 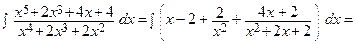
= 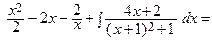
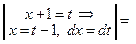
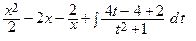 =
=
= 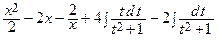 =
= 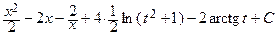 =
=
= 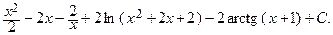
Отметим, что любая рациональная функция интегрируется в элементарных функциях.
Интегрирование иррациональных функций
Интегралы от квадратичных иррациональностей
Интегралы типа  ,
, 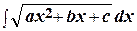 ,
, 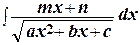 называются неопределенными интегралами от квадратичных иррациональностей.
называются неопределенными интегралами от квадратичных иррациональностей.
Их можно найти следующим образом: под знаком радикала выделить полный квадрат:
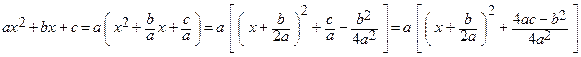
и сделать подстановку 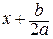 = t. При этом первые два интеграла приводятся к табличным, а третий – к сумме двух табличных интегралов.
= t. При этом первые два интеграла приводятся к табличным, а третий – к сумме двух табличных интегралов.
Пример 8. Найти интеграл 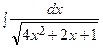 .
.
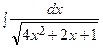 =
= 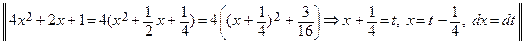 =
=
= 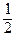
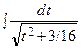 =
= 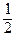 ln
ln 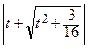 + C =
+ C = 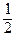 ln
ln 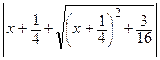 + C.
+ C.
Пример 9. Найти интеграл 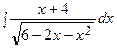 .
.
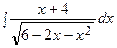 =
= 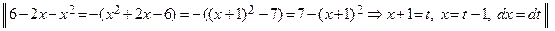 =
=
= 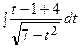 =
= 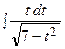 + 3
+ 3  = –
= – 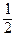
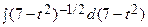 + 3
+ 3 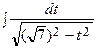 =
=
= – 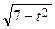 + 3arcsin
+ 3arcsin 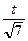 + C = 3arcsin
+ C = 3arcsin 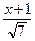 –
– 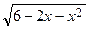 + C.
+ C.
Интегралы типа 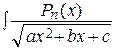 dx, где Pn (x)– многочлен степени n, удобно вычислять, пользуясь формулой
dx, где Pn (x)– многочлен степени n, удобно вычислять, пользуясь формулой
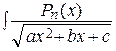 dx = Qn – 1(x) ·
dx = Qn – 1(x) · 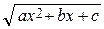 + An
+ An 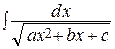 . (1)
. (1)
Здесь Qn – 1(x) = A 0 + A 1 х +…+ An – 1 х n – 1 – многочлен степени n с неопределенными коэффициентами.
Для нахождения коэффициентов A 0, A 1, …, An продифференцируем обе части (1)
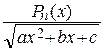 = Q′n – 1(x) ·
= Q′n – 1(x) · 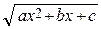 + Qn – 1(x) ·
+ Qn – 1(x) · 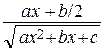 + An
+ An 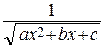 (2)
(2)
Затем правую часть равенства (2) приводим к общему знаменателю, равному знаменателю левой части, т.е. 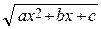 , сокращая на который обе части (2), получим тождество
, сокращая на который обе части (2), получим тождество
Pn (x)= Q′n – 1(x) · (ax 2 + bx + c) + Qn – 1(x) · (ax + b /2) + An, (3)
в обеих частях которого стоят многочлены степени n. Приравнивая коэффициенты при одинаковых степенях х в левой и правой частях (3), получим n + 1 уравнений, из которых находим искомые коэффициенты Ak, k = 0, 1, 2, …, n. Подставляя их значения в правую часть (1) и найдя интеграл 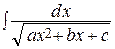 , (см. выше) получим ответ для данного интеграла.
, (см. выше) получим ответ для данного интеграла.
Пример 10. Найти интеграл 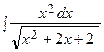 .
.