Тематика решаемых задач.
Практическое занятие по теме ПМ – МА.9 «Методика исследования функций на непрерывность. Построение схематического графика функции» предполагает применение теоретических положений данной темы к исследованию функции на непрерывность, определение точек разрыва, установление характера разрыва и схематического построения графика функции на основании полученных результатов исследования.
Вам необходимо уметь:
- В зависимости от аналитического выражения функции применить то или иное определение непрерывности функции.
- По виду функции определять точки разрыва, т.е. точки в которых функция не определена.
- Определять характер разрыва.
- Исследовать «поведение» функции на бесконечности, т.е. при х ® ±¥.
- Строить схематический график исследуемой функции.
Структурно – логическая схема тематики решаемых задач.
 |
Пример 1. Пользуясь вторым определением непрерывности, доказать, что функция
f (х) = 2 х 2 – 3 х + 4 непрерывна в точке х 0 = 1.
Решение. Заданная функция определена в точке х 0 = 1 и ее окрестности. Мы должны показать, что бесконечно малому приращению аргумента в точке х 0 = 1 соответствует бесконечно малое приращение функции, то есть
 , где D f (х 0) = f (х 0 + D х) – f (х 0), D х = х – х 0.
, где D f (х 0) = f (х 0 + D х) – f (х 0), D х = х – х 0.
Вычислим значение функции в точке х 0 = 1 f (х 0) = f (1) = 2×12 – 3×1 + 4 = 2 – 3 + 4 = 3.
Дадим х 0 приращение D х и найдем значение функции при х = х 0 + D х = 1 + D х.
f (х 0 + D х) = f (1 + D х) = 2×(1 + D х)2 – 3××(1 + D х) + 4 = 2 (1 + 2× D х + (D х)2) – 3 – 3 D х + 4 =
= 2 + 4× D х + 2 (D х)2 – 3 – 3 D х + 4 = 2 (D х)2 + D х + 3.
Теперь найдем приращение функции в точке х 0 = 1
D f (х 0) = D f (1) = f (х 0 + D х) – f (х 0) = f (1 + D х) – f (1) = 2 (D х)2 + D х + 3 – 3 = 2 (D х)2 + D х
Вычислим предел приращения функции при условии, что приращение аргумента D х ® 0
 .
.
Это и доказывает непрерывность заданной функции в точке х 0 = 1.
Пример 2. Каков характер разрыва функции
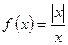
в точке х = 0?
Решение. В этой точке функция разрывна, так как f (0) не существует. Вычислим односторонние пределы при х ® 0 - e и х ® 0 + e, где e > 0, e ® 0, то есть e - бесконечно малая положительная величина

 .
.
Следовательно, односторонние пределы функции в точке х = 0 существуют, но не равны между собой, f (0 + e) ¹ f (0 - e), поэтому в точке х = 0 функция терпит разрыв 1-го рода. Величина скачка 1 – (-1) = 2. Схематический график функции имеет вид

Пример 3. Исследовать на непрерывность и построить схематический график функции
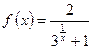 .
.
Решение. В точке х = 0 функция не существует. Следовательно, в этой точке нарушено условие непрерывности и х = 0 является точкой разрыва. Для определения характера разрыва найдем односторонние пределы.
Правосторонний предел:
 .
.
Действительно, так как e > 0 и e ® 0, то 1/ e - бесконечно большая положительная величина, тогда  - также бесконечно большая величина, а обратная ей величина
- также бесконечно большая величина, а обратная ей величина
 -
-
бесконечно малая, то есть ее предел равен нулю.
Левосторонний предел:
 .
.
Действительно, так как e > 0 и e ® 0, то 1/ e - бесконечно большая положительная величина, а
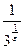 -
-
бесконечно малая, то есть ее предел равен нулю.
Следовательно, в точке х = 0 имеет место разрыв 1-го рода, так как
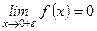 ,
, 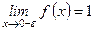 и
и 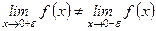 .
.
Чтобы построить схематичный график заданной функции, уточним ее поведение при х ® ±¥. В этом случае
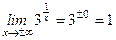 .
.
Следовательно,
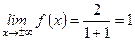 .
.
Это означает, что на бесконечности график функции асимптотически приближается к прямой у = 1. График функции схематически изображен на рисунке

Пример 4. Найти точки разрыва функции и установить их характер
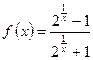 .
.
Решение. Заданная функция не существует в точке х = 0. Следовательно, нарушается условие непрерывности функции в точке х = 0, а, значит, эта точка является точкой разрыва. Чтобы установить характер разрыва, вычислим односторонние пределы.
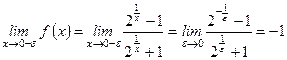 .
.
Здесь, 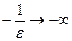 при e ® 0, а
при e ® 0, а  .
.
 .
.
При e ® 0 имеем неопределенность вида (¥/¥), т.к. 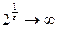 , при e ® 0. Чтобы раскрыть эту неопределенность, разделим почленно числитель и знаменатель дроби на
, при e ® 0. Чтобы раскрыть эту неопределенность, разделим почленно числитель и знаменатель дроби на 
 .
.
Здесь 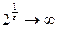 при e ® 0, а
при e ® 0, а 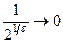 .
.
В точке х = 0 имеем разрыв первого рода. Установим поведение функции при х ® ±¥.
 ,
,
т.е. график асимптотически приближается к оси Ох.
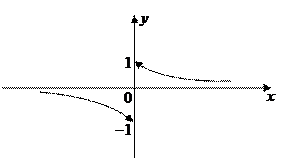
Пример 5. Найти точки разрыва и построить схематический график функции
 .
.
Решение. Функция в точке х = 1 не определена, значит, эта точка является точкой разрыва. Найдем односторонние пределы функции в точке х = 1.
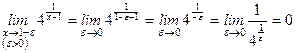 .
.
 .
.
Правосторонний предел равен бесконечности, поэтому х = 1 – точка разрыва 2-го рода. На бесконечности график функции асимптотически приближается к прямой у = 1, так как
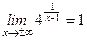 .
.
Схематический график исследуемой функции имеет вид
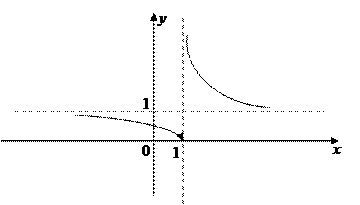 |
Пример 6. Найти точки разрыва функции и построить схематический график функции
 .
.
Решение. Функция определена при всех значениях х, кроме х = ±1. Эта функция элементарна, поэтому она непрерывна во всей области своего определения:
х Î (-¥; -1) È (-1; 1) È (1; +¥).
Вычислим односторонние пределы:

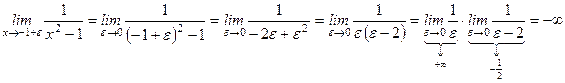

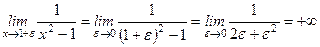 .
.
Следовательно, в точках х = ±1 бесконечный разрыв, т.е. разрыв 2-го рода. Следует отметить, что при х ® ±¥, f (х) ® 0, т.е. график функции приближается асимптотически к оси Ох. Кроме того, график пересекает ось Оу в точке у = -1.
 |
Пример 7. Исследовать на непрерывность и найти точки разрыва функции
 ,
,
построить схематический график.
Решение. Функция определена, т.е. может быть вычислена при всех значениях х, кроме
х = 0. Вычислим односторонние пределы

 .
.
Следовательно, функция в точке х = 0 имеет устранимый разрыв. При х ® ±¥ функция стремится к единице

Доопределим функцию, чтобы она стала непрерывной
 .
.
Пример 8. Найти точки разрыва функции и установить их характер
 .
.
Решение. Функция не определена в точках х = ±2. Найдем односторонние пределы

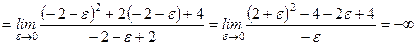 ;
;
 .
.
В точке х = -2 функция терпит разрыв 2-го рода

 .
.
В точке х = 2 устранимый разрыв.
Пример 9. Исследовать на непрерывность и построить схематичный график
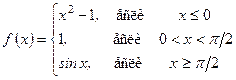 .
.
Решение. Данная функция составлена из элементарных функций, которые непрерывны на всей числовой оси. Точками возможного разрыва могут быть только точки, в которых изменяется аналитическое выражение функции, то есть х = 0 и х = p /2.
В окрестности точки х = 0 функция определена двумя различными выражениями: слева и в самой точке х = 0 f (х) = х 2 – 1, справа – f (х) = 1. Вычислим односторонние пределы

 .
.
Значение функции в точке х = 0 равно
 .
.
Следовательно, односторонние пределы существуют, конечны, но не равны между собой. Таким образом, в точке х = 0 функция имеет разрыв 1-го рода. Скачок равен 2.
В окрестности точки х = p /2 функция задается также двумя различными аналитическими выражениями: слева f (х) = 1, а справа и в самой точке х = p /2 f (х) = sin x
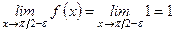
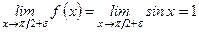 .
.
Здесь односторонние пределы конечны, равны между собой и равны значению функции в точке
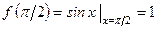 .
.
Следовательно, в точке х = p /2 функция непрерывна.
Схема проведенного анализы наглядно иллюстрируется следующей условной графической интерпретацией
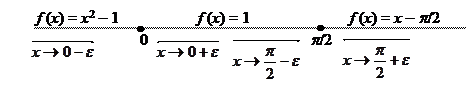
Схематический график заданной функции имеет вид.
 |
Пример 10. Подобрать числа а и b такие, чтобы функция

была непрерывной.
Решение. Для того чтобы функция была непрерывной в точке х = 1, должно выполняться условие
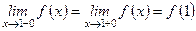
Найдем односторонние пределы
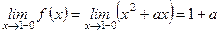
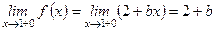 .
.
Кроме того, f (1) = 1 + а. Следовательно, чтобы функция была непрерывной, должно выполняться равенство 1 + а = 2 + b или а – b = 1. Это уравнение содержит две независимые величины а и b. Поэтому одной из них мы даем произвольное значение, а вторую находим из имеющегося соотношения. Например, а = 0, тогда b = -1 или а = 2, то b = 1 и т.д.
Самостоятельная работа.
- Доказать, что функция f (х) непрерывна в точке х 0, используя определение непрерывности функции в точке на языке приращений, т.е.
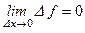 .
.
а) f (х) = 4 х 2 + 2, х 0 = 2
б) 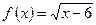 , х 0 = 7
, х 0 = 7
- Доказать, что функция f (х) имеет разрыв в точке х 0 = 0, и построить график функции, если
а) 
б) 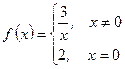
- Найти точки разрыва функции и установить их характер:
а)  Ответ: х = -2–т. разрыва 1-го рода скачок равен 2
Ответ: х = -2–т. разрыва 1-го рода скачок равен 2
б) 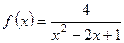 Ответ: х = 1 т. разрыва 2-го рода
Ответ: х = 1 т. разрыва 2-го рода
в)  Ответ: х = 0 – т. разрыва 2-го рода,
Ответ: х = 0 – т. разрыва 2-го рода,
х = 1 – т. разрыва 1-го рода
г)  Ответ: х =6 разрыв 2-го рода, х =-6 устранимый разрыв
Ответ: х =6 разрыв 2-го рода, х =-6 устранимый разрыв
д) f (х) = ln (2 х + 1) Ответ: 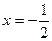 - т. разрыва 2-го рода
- т. разрыва 2-го рода
- Найти точки разрыва и построить схематический график
а) 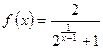 Ответ: х = 1 – т. разрыва 1-го рода
Ответ: х = 1 – т. разрыва 1-го рода
б) 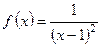 Ответ: х = 1 – т. разрыва 2-го рода
Ответ: х = 1 – т. разрыва 2-го рода
в) 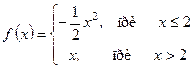 Ответ: х = 2 т. разрыва 1-го рода
Ответ: х = 2 т. разрыва 1-го рода
г) 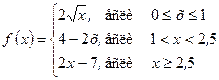 Ответ: х = 1 – т. непрерывности
Ответ: х = 1 – т. непрерывности
х = 2,5 – т. разрыва 1-го рода
д)  Ответ: х = –1 разрыв 1-го рода
Ответ: х = –1 разрыв 1-го рода
х = 1 разрыв 2-го рода
- Следующие функции требуется доопределить в точке х = 0, чтобы они стали непрерывными
а) 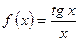 Ответ: f (0) = 1
Ответ: f (0) = 1
б)  Ответ: f (0) = -3/2
Ответ: f (0) = -3/2
в) 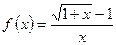 Ответ: f (0) = 1/2
Ответ: f (0) = 1/2
г)  Ответ: f (0) = 2
Ответ: f (0) = 2