МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Специальность
Прикладная математика и информатика
УТВЕРЖДАЮ
Зав. кафедрой дифференциальныхуравнений
Проф. Шашкин А. И.
«» ______________________ 2007 г.
РАБОЧАЯ ПРОГРАММА
1. Шифр и наименование специальности:
010501 Прикладная математика и информатика
2. Уровень образования: Высшее профессионально образование
3. Форма обучения: Очная
4. Код и наименование дисциплины (в соответствии с учебным планом):
ЕН. Ф. 01. 1.1. Математический анализ
5. Кафедра, отвечающая за дисциплину:
Кафедра дифференциальных уравнений
6. Составители:
Мешков В.З., д.ф.-м.н., профессор, факультет ПММ, кафедра дифференциальных уравнений,
Ларин А.А., к.ф.-м.н., доцент, факультет ПММ, кафедра дифференциальных уравнений,
Половинкин И.П., к.ф.-м.н., доцент, факультет ПММ, кафедра дифференциальных уравнений,
Виноградова Г.А., к.ф.-м.н., доцент, факультет ПММ, кафедра дифференциальных уравнений,
7. Кем рекомендовано к использованию в учебном процессе:
Кафедрой дифференциальных уравнений
Протокол о рекомендации № 1 от 9 сентября 2005 г.
8. Учебный год: 2005/2006, семестр 1,2,3,4
Количество часов, отводимых на изучение дисциплины в
соответствии с планом учебного процесса:
Аудиторные занятия: 420, в том числе:
лекции: 210
практики: 210
Самостоятельная работа: 250
Всего часов: 670
10. Количество контрольных работ, предусмотренных учебным планом: 16
11. Формы итогового контроля:
Зачёт - 1,2,3,4 семестр,
Экзамен - 1,2,3,4 семестр
12. Тематика (по ГРНТИ): Математика
13. Поисковый образ (ключевые слова):
последовательность; предел последовательности; функция; непрерывность; предел функции; производная; дифференциал; формула Тейлора; правило Лопиталя; интеграл; несобственный интеграл; числовой ряд; функциональный ряд; ряд Фурье; криволинейный интеграл; экстремум; условный экстремум
14. Цели и задачи изучения дисциплины:
Цель курса сообщить сведения по математическому анализу в объеме, необходимом для изучения смежных дисциплин физико-математического цикла и для свободной ориентации в вопросах анализа и его приложений, которые могут встретиться в теоретической и практической работе; выработать навыки применения основных методов и приемов математического анализа для решения конкретных задач. Задачи курса – усвоение основных идей и фактов дифференциального и интегрального исчисления, теории меры и интеграла и элементов комплексного и гармонического анализа. Имеется в виду достаточно глубокая проработка теоретических аспектов и практическая сторона предмета.
15. Основные знания, умения и навыки, которыми студент должен овладеть в результате изучения дисциплины:
В процессе обучения студенты должны изучить такие понятия математического анализа как последовательность, функция (функция многих переменных), интеграл (неопределенный, определенный, n- кратный, криволинейный, поверхностный, несобственный, зависящий от параметра), ряд (числовой, функциональный, Фурье); приобрести навыки вычислений пределов последовательностей и функций, навыки доказательств основных теорем о пределах; навыки вычисления производных, применения аппарата дифференциального исчисления к исследованию функций, вычислению пределов функций, навыки доказательств основных теорем дифференциального исчисления, навыки вычисления интегралов, навыки доказательства основных теорем интегрального исчисления, навыки доказательств основных теорем о числовых и функциональных рядах, в том числе о степенных рядах и рядах Фурье, навыки исследования вопроса сходимости ряда.
ТЕМАТИЧЕСКИЙ ПЛАН И СЕТКА ЧАСОВ ДИСЦИПЛИНЫ
| № п/п | Название темы* | Лекции (час) | Практич. занятия (час) | Лаборат. занятия (час) | Самост. работа (час) | Формы текущего контроля |
| Введение | проверка д.з., опрос | |||||
| Теория последовательностей | проверка д.з., опрос, к.р. | |||||
| Пределы функций | проверка д.з., опрос, к.р. | |||||
| Дифференциальное исчисление функций вещественной переменной | проверка д.з., опрос, к.р. | |||||
| Первообразная функции и неопределенный интеграл | проверка д.з., опрос, к.р. | |||||
| Определенный интеграл Римана | проверка д.з., опрос, к.р. | |||||
| Несобственные интегралы | проверка д.з., опрос, к.р. | |||||
| Числовые ряды | проверка д.з., опрос, к.р. | |||||
| Функциональные последовательности и ряды | проверка д.з., опрос, к.р. | |||||
| Ряды Фурье | проверка д.з., опрос, к.р. | |||||
| Функции нескольких переменных | проверка д.з., опрос, к.р. | |||||
| Интегралы, зависящие от параметра | проверка д.з., опрос, к.р. | |||||
| Несобственные интегралы, зависящие от параметра | проверка д.з., опрос, к.р. | |||||
| Криволинейные интегралы | проверка д.з., опрос, к.р. | |||||
| Двойные и n-кратные интегралы | проверка д.з., опрос, к.р. | |||||
| Поверхностные интегралы | проверка д.з., опрос, к.р. | |||||
| Элементы теории поля | проверка д.з., опрос, к.р. | |||||
| Несобственные кратные интегралы | проверка д.з., опрос | |||||
| Интеграл Стилтьеса. Интеграл Лебега. | проверка д.з., опрос |
Рабочая программа дисциплины должна соответствовать Государственному образовательному стандарту высшего профессионального образования и Плану учебного процесса соответствующей специальности (направления)
УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА ДИСЦИПЛИНЫ
Лекции
| № темы | № лекции | План лекции | Ссылки на литературу* для обязательного изучения | Ссылки на литературу* для самостоятельной работы | Формы текущего контроля |
| 1. | Множества и операции над ними. Понятия отображения, функции. Сюръективные, инъективные и биективные отображения. Понятие обратной функции и сложной функции. Использование специальных и логических символов. | [2], Т.1, С.5-15 | [2], Т.1, С.5-15 | ||
| 2. | Вещественные числа и их основные свойства. Абсолютная величина вещественного числа. Аксиома полноты (непрерывности). Числовые множества, понятие расширенной числовой прямой, окрестности, промежутки. Ограниченные и неограниченные множества. Точные верхние и нижние грани числовых множеств, их существование | [2], Т..1, С.15-20, 27-30,33-42 | [2], Т..1, С.15-20, 27-30, 33-42 | ||
| 3. | Символы n!, n!!, Cnk. Бином Ньютона. Принцип вложенных отрезков. Равномощные множества. Счетные и несчетные множества. Теорема Кантора. | [2], Т.1, С.44-48. 82-85 | [2], Т.1, С.44-48. 82-85 | ||
| 4. | Числовые последовательности. Определение предела числовой последовательности. Вычисление пределов на основе определения предела числовой последовательности. Сходящиеся, расходящиеся, бесконечно большие последовательности. Единственность предела числовой последовательности. Ограниченность сходящейся последовательности. | [2], Т.1, С.48-55, 59-60 | [2], Т.1, С.48-55, 59-60 | ||
| 5. | Переход к пределу в неравенствах. Понятие подпоследовательности. Лемма о пределе подпоследовательности. | [2], Т.1, С.56-59 | [2], Т.1, С.56-59 | ||
| 6. | Монотонные последовательности. Теорема Вейерштрасса. Число e. Теорема Больцано-Вейерштрасса (свойство компактности ограниченной последовательности). Частичные пределы. | [2], Т.1, С. 60-65 | [2], Т.1, С.60-65 | ||
| 7. | Фундаментальные последовательности и критерий Коши. Бесконечно малые последовательности. Свойства пределов, связанные с арифметическими действиями над последовательностями. | [2], Т.1, С. 65-72 | [2], Т.1, С. 65-72 | ||
| 8. | Верхний и нижний пределы последовательности. Теорема существования. Необходимое и достаточное условие того, что b (a) -- верхний (нижний) предел числовой последовательности. Критерий существования предела. | [2], Т.1, С.86-89 | [2], Т.1, С.86-89 | ||
| 9. | Числовые функции. Точки прикосновения, изолированные точки и предельные точки множеств. Определение предела функции в точке по Гейне. Свойство “локальности” предела. Условие существования предела (метод “смешивания”). Определение предела функции по Коши. | [2], Т.1, С.89-106 | [2], Т.1, С.89-106 | ||
| 10. | Критерий Коши существования предела функции в точке. Свойства пределов функций. | [2], Т.1, С.107-110, С. 113-115 | [2], Т.1, С.107-110, С. 113-115 | ||
| 11. | Бесконечно малые и бесконечно большие функции, их основные свойства. Сравнение функций в окрестности точки. О – символика (символы Ландау). Понятие асимптотического равенства. Главная часть функции в точке. | [1], Ч.1, С.119-121, [2], Т.1, С.144-154 | [1], Ч.1, С.119-121, [2], Т.1, С.144-154 | ||
| 12. | Различные формы записи непрерывности функции в точке. Функции, разрывные в точке. Классификация точек разрыва функций. Понятие одностороннего разрыва. Непрерывность функции на множестве. | [1], Ч.1, С.127-131, 162-166 | [1], Ч.1, С.127-131, 162-166 | ||
| 13. | Теорема о пределах монотонной функции. Разрывы монотонной функции. Условие непрерывности монотонной функции. Предел и непрерывность композиции функций. | [2], Т.1, С.111-113, 120, [5], Т.1, С.154,155 | [2], Т.1, С.111-113, 120, [5], Т.1, С.154,155 | ||
| 14. | Теорема Больцано-Коши и следствие из нее. Теорема существования, монотонности и непрерывности обратной функции у монотонной непрерывной функции. Теорема Вейерштрасса. | [2], Т.1, С. 121-129 | [2], Т.1, С. 121-129 | ||
| 15. | Элементарные функции и их непрерывность. Замечательные пределы. | [2], Т.1, С. 131-144 | [2], Т.1, С. 131-144 | ||
| 16. | Понятие равномерной непрерывности. Теорема Кантора. Колебание функции на промежутке. | [1], Ч.1, С.176-180 | [1], Ч.1, С.176-180 | ||
| 17. | Производная функции в точке. Определение односторонних производных. Производные на концах промежутка. Определение функции, дифференцируемой в точке. Дифференциал функции. Критерий дифференцируемости. Дифференциал аргумента функции. Непрерывность дифференцируемой функции. | [1], Ч.1, С.189-197 | [1], Ч.1, С.189-197 | ||
| 18. | Дифференцировние суммы, произведения и частного дифференцируемых функций. Дифференцирование обратной функции. Дифференцирование сложной функции. Инвариантность формы первого дифференциала. | [1], Ч.1, С.197-205 | [1], Ч.1, С.197-205 | ||
| 19. | Производные высших порядков. Формула Лейбница. Дифференциалы высших порядков. Нарушение инвариантности формы дифференциалов высших порядков. | [1], Ч.1, С.213-220 | [1], Ч.1, С.213-220 | ||
| 20. | Теоремы Ферма, Ролля, Лагранжа и Коши. | [2], Т.1, С. 192-201 | [2], Т.1, С. 192-201 | ||
| 21. | Раскрытие неопределенностей по правилу Лопиталя. | [2], Т.1, С. 201-205 | [2], Т.1, С. 201-205 | ||
| 22. | Формула Тейлора для многочлена. Разложение произвольных функций: формула Тейлора с дополнительным членом в форме Лагранжа, Коши и Пеано. Единственность многочлена Тейлора. Примеры разложений по формуле Тейлора. | [3] Т.1, С. 183-190, [2], Т.1, С. 214-215 | [3] Т.1, С. 183-190, [2], Т.1, С. 214-215 | ||
| 23. | Применение дифференциального исчисления к исследованию функций. Необходимое и достаточное условие монотонности функции на интервале. Достаточное условие строгой монотонности. Локальные экстремумы функций. Достаточное условие локального экстремума функции в терминах смены производной. Достаточное условие локального экстремума функции, имеющей производные высших порядков. | [2], Т.1, С. 221-230 | [2], Т.1, С. 221-230 | ||
| 24. | Понятие выпуклости функции. Определение точек перегиба. Необходимое и достаточное условие выпуклости функции. Нахождение точек перегиба. | [5], Т.1, С. 294-305 | [5], Т.1, С. 294-305 | ||
| 25. | Асимптоты графика функции. Исследование функций и построение графиков функций. | [2], Т.1, С. 236-241 | [2], Т.1, С. 236-241 | ||
| 26. | Функции, заданные параметрически. Вычисление производных высших порядков от параметически заданных функций. | [2], Т.1, С. 188-192 | [2], Т.1, С. 188-192 | ||
| Исследование функций, заданных параметрически и построение их графиков. | [2], Т.1, С. 242-248 | [2], Т.1, С. 242-248 | ЭКЗАМЕН | ||
| 28. | Определение первообразной функции. Свойства первообразной функции. Неопределенный интеграл. Свойства неопределенного интеграла Табличное интегрирование | [2], Т.1, С. 378-384 | [2], Т.1, С. 378-384 | ||
| 29. | Интегрирование подстановкой и по частям. Интегрирование рациональных функций | [2], Т.1, С. 384-389, 412-416 | [2], Т.1, С. 384-389, 412-416 | ||
| 30. | Интегрирование рациональной функции от степеней дробно-линейной функции. Интегрирование функций, содержащих корень из квадратного трехчлена. Подстановки Эйлера. | [2], Т.1, С. 421-426 | [2], Т.1, С. 421-426 | ||
| 31. | Интегрирование дифференциального бинома. Интегрирование тригонометрических функций. Универсальная тригонометриче ская подстановка. Обзор частных случаев. | [2], Т.1, С. 426-428, 431-434 | [2], Т.1, С. 426-428, 431-434 | ||
| 32. | Интегралы от трансцендентных функций, вычисляемые с помощью интегрирования по частям Интегрирование гиперболических функций | [2], Т.1, С. 434-436 | [2], Т.1, С. 434-436 | ||
| 33. | Некоторые специальные приёмы вычисления интегралов Неопределенные интегралы, не выражающиеся через элементарные функции. | [2], Т.1, С. 436-438, [5], Т.2, С. 66- 72 | [2], Т.1, С. 436-438, [5], Т.2, С. 66- 72 | ||
| 34. | Интегрируемость функции по Риману. Определение определенного интеграла Римана в терминах интегральных сумм Римана. Геометрический смысл интегральной суммы Римана. Интегрируемость постоянной на отрезке функции. Ограниченность интегрируемой на отрезке функции. Неинтегрируемость функции Дирихле. | [1], Ч.1, С.330-333 | [1], Ч.1, С.330-333 | ||
| 35. | Верхние и нижние суммы Дарбу. Геометрический смысл сумм Дарбу. Свойства сумм Дарбу: оценки интегральных сумм Римана, приближение сумм Дарбу суммами Римана, монотонность сумм Дарбу, неравенства для верхних и нижних сумм Дарбу различных разбиений. Ограниченность сумм Дарбу. | [1], Ч.1, С.334-337 | [1], Ч.1, С.334-337 | ||
| 36. | Верхний и нижний интегралы Дарбу. Определение. Лемма о неравенстве для верхнего и нижнего интегралов Дарбу. Лемма об оценке разности сумм Дарбу разбиения и его измельчения. Понятие предела суммы Дарбу. Основная лемма Дарбу. | [1], Ч.1, С.337-339 | [1], Ч.1, С.337-339 | ||
| 37. | Необходимое и достаточное условие интегрируемости по Риману ограниченной функции в терминах верхнего и нижнего интегралов Дарбу (вспомогательная теорема). Основная теорема о необходимом и достаточном условии интегрируемости по Риману ограниченной на отрезке функции. | [1], Ч.1, С.339-341 | [1], Ч.1, С.339-341 | ||
| 38. | Интегрируемость непрерывных и монотонных на отрезке функций. Достаточное условие интегрируемости разрывной ограниченной функции. Следствия. Пример интегрируемой функции, имеющей бесконечно много точек разрыва. | [1], Ч.1, С.341-344 | [1], Ч.1, С.341-344 | ||
| 39. | Интегрируемость сложной функции. Следствие. Простейшие свойства определенного интеграла Римана (линейность, интегрируемость произведения, интегрируемость на подмножествах, аддитивность определенного интеграла). | [1], Ч.1, С.344-350 | [1], Ч.1, С.344-350 | ||
| 40. | Свойства интеграла Римана, связанные с неравенствами. Формулы среднего значения для определенного интеграла Римана. | [1], Ч.1, С.350-353 | [1], Ч.1, С.350-353 | ||
| 41. | Интеграл с переменным верхним пределом. Дифференцируемость интеграла с переменным верхним пределом. Существование первообразной у непрерывной функции. Дифференцирование интеграла с переменным пределом. Непрерывность интеграла с переменным верхним пределом. | [1], Ч.1, С.357-359 | [1], Ч.1, С.357-359 | ||
| 42. | Формула Ньютона-Лейбница. Методы вычисления определенного интеграла (интегрирование подстановкой и по частям). Формула Тейлора с остаточным членом в интегральной форме. | [1], Ч.1, С.359-363 | [1], Ч.1, С.359-363 | ||
| 43. | Приложения определенного интеграла к вычислению площади криволинейной трапеции и площади криволинейного сектора. Экономические и физические приложения. | [1], Ч.1, С.405-416 | [1], Ч.1, С.405-416 | ||
| 44. | Приложения определенного интеграла к вычислению объема тела вращения и к вычислению длины дуги. | [1], Ч.1, С.391-403, 418-421 | [1], Ч.1, С.391-403, 418-421 | ||
| 45. | Несобственные интегралы первого и второго рода. Определение, примеры. Главное значение несобственного интеграла. Критерий Коши сходимости несобственного интеграла. Абсолютная и условная сходимость. Общий признак сравнения для несобственных интегралов в форме неравенств и в предельной форме. Частные признаки сравнения для несобственных интегралов первого и второго рода в форме неравенств и в предельной форме. | [1], Ч.1, С.371-376 | [1], Ч.1, С.371-376 | ||
| 46. | Признак Дирихле-Абеля сходимости несобственного интеграла. Замена переменной и интегрирование по частям в несобственных интегралах. | [1], Ч.1, С.376-384 | [1], Ч.1, С.376-384 | ||
| 47. | Числовой ряд. Сходимость. Критерий Коши сходимости числового ряда. Необходимое условие сходимости. Необходимое и достаточное условие сходимости в терминах остатка. Простейшие свойства и признаки сходимости числовых рядов. Абсолютная сходимость числового ряда | [3], Т.2, С.11-15, 29-30 | [3], Т.2, С.11-15, 29-30 | ||
| 48. | Числовые ряды с неотрицательными членами. Необходимое и достаточное условие сходимости. Признак Коши. Признаки Раабе и Гаусса (без доказательства). Признаки сравнения сходимости числовых рядов с неотрицательными членами в форме неравенств и в предельной форме. Интегральный признак сходимости числового ряда с неотрицательными членами. Расходимость гармонического ряда. | [3], Т.2, С.15-28 | [3], Т.2, С.15-28 | ||
| 49. | Знакочередующиеся ряды. Признак Лейбница сходимости знакочередующегося ряда. Преобразование Абеля. Признаки Дирихле и Абеля сходимости знакопеременных рядов. Теорема о перестановке членов абсолютно сходящегося ряда. Сочетательное свойство сходящегося ряда. Теорема Римана о перестановке членов условно сходящегося ряда. Теорема о перемножении абсолютно сходящихся рядов. | [3], Т.2, С.32-42, [1], Ч. 2, С 36-39 | [3], Т.2, С.32-42, [1], Ч. 2, С 36-39 | ||
| 50. | Поточечная и равномерная сходимость функциональных последовательностей и рядов. Критерий Коши равномерной сходимости. Признак Вейерштрасса равномерной сходимости функционального ряда. Признак Дирихле равномерной сходимости функционального ряда. Признак Абеля. Почленный переход к пределу в функциональной последовательности и функциональном ряде. Непрерывность суммы равномерно сходящегося функционального ряда, состоящего из непрерывных функций. Теорема Дини. Почленное интегрирование функциональных последовательностей и рядов. Почленное дифференцирование функциональных последовательностей и рядов. | [1], Ч. 2, С 67 -93 | [1], Ч. 2, С 67 -93 | ||
| 51. | Определение степенного ряда. Теорема Коши-Адамара. Теорема о радиусе сходимости степенных рядов, полученных почленным дифференцированием и интегрированием степенного ряда. Следствие. Вещественно аналитические функции. Единственность разложения в степенной ряд. Ряд Тейлора. Пример бесконечно дифференцируемой неаналитической функции. Достаточное условие разложимости функции в степенной ряд. | [1], Ч. 2, С 102-108 | [1], Ч. 2, С 102-108 | ||
| 52. | Разложение в ряд Тейлора показательной, логарифмической, гиперболических, тригонометрических функций. Биномиальный ряд. Разложение функций в степенные ряды методом почленного дифференцирования и интегрирования. | [1], Ч. 2, С 108-110, [2], Т. 1, С.636-649 | [1], Ч. 2, С 108-110, [2], Т. 1, С.636-649 | ЭКЗАМЕН | |
| 53. | Определение ряда Фурье для абсолютно интегрируемой функции. Предложение о стремлении к нулю при   интегралов вида интегралов вида  , ,  от абсолютно интегрируемой функции f(x). Лемма об аппроксимации. Лемма Римана. от абсолютно интегрируемой функции f(x). Лемма об аппроксимации. Лемма Римана.
| [2,т.2 ] С.267-274 | [2,т.2 ] С.267-274 | ||
| 54. | Ядро Дирихле и его свойства. Интеграл Дирихле. Принцип локализации. Сходимость рядов Фурье для кусочно-дифференцируемых функций. | [2,т.2 ] С.274-284, [3,т.2 ] С.383-384 | [2,т.2 ] С.274-284, [3,т.2 ] С.383-384 | ||
| 55. | Суммирование рядов Фурье методом средних арифметических. Свойства ядер Фейера. Теорема о сходимости сумм Фейера. | [2,т.2 ]С.2847-287 | [2,т.2 ]С.2847-287 | ||
| 56. | Теорема Вейерштрасса-Стоуна о приближении непрерывной на отрезке функции алгебраическими многочленами. Полнота систем функций в смысле равномерного приближения. Теорема о полноте тригонометрической системы и системы целых неотрицательных степеней x. | [2,т.2 ] С.290-292 | [2,т.2 ] С.290-292 | ||
| 57. | Полнота в смысле среднего квадратичного приближения. Полнота тригонометрической системы функций и системы целых неотрицательных степеней x для множества непрерывных функций. | [2,т.2 ] С.267-274 [3,т.2 ] С.413-416 | [2,т.2 ] С.267-274 [3,т.2 ] С.413-416 | ||
| 58. | Минимальное свойство коэффициентов Фурье. Неравенство Бесселя. Равенство Парсеваля и следствия из него (случай непрерывной функции). | [2,т.2 ] С.292-296 [3,т.2 ] С.409-412 | [2,т.2 ] С.292-296 [3,т.2 ] С.409-412 | ||
| 59. | Почленное дифференцирование рядов Фурье. Предложение о порядке убывания коэффициентов Фурье при 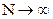 . Достаточное условие равномерной сходимости ряда Фурье. . Достаточное условие равномерной сходимости ряда Фурье.
| [2,т.2 ] С.296-301 [3,т.2 ] С.418-419 | [2,т.2 ] С.296-301 [3,т.2 ] С.418-419 | ||
| 60. | Определение N-мерного евклидова пространства Е. Основные понятия и определения. Свойства расстояния в Е. | [2,т.1 ] С.267-274 | [2,т.1 ] С.267-274 | ||
| 61. | Последовательности точек в Е. Сходящиеся последовательности и их свойства. Критерий Коши сходимости последовательности точек в Е. Теорема Больцано-Вейерштрасса. Предельные точки множества. Открытые и замкнутые множества. Операция замыкания. Компакты в Е. | [2,т.1 ] С.274-291 | [2,т.1 ] С.274-291 | ||
| 62. | Функции нескольких действительных переменных. Определение предела функции в точке. Арифметические свойства пределов функций. Критерий Коши существования конечного предела функции n переменных. Повторные пределы. | [2,т.1 ] С.291-298 | [2,т.1 ] С.291-298 | ||
| 63. | Непрерывность функции n переменных. Арифметические операции над непрерывными функциями. Свойства непрерывных функций (теорема об устойчивости знака, теорема о прохождении непрерывной функции через любое промежуточное значение, теорема Вейерштрасса.) Равномерная непрерывность функций. Теорема Кантора. | [2,т.1 ] С.229-308 | [2,т.1 ] С.229-308 | ||
| 64. | Частные производные функции нескольких переменных Дифференцируемость в точке. Связь дифференцируемости с существованием частных производных. Геометрический смысл условия дифференцируемости в случае функций двух переменных. Достаточные условия дифференцируемости. Понятие дифференциала. Дифференцируемость сложной функции и инвариантность формы первого дифференциала. Производная по направлению. Градиент. | [2,т.1 ] С.310-321 | [2,т.1 ] С.310-321 | ||
| 65. | Частные производные и дифференциалы высших порядков. Теорема о равенстве смешанных производных. | [2,т.1 ] С.322-339 | [2,т.1 ] С.322-339 | ||
| 66. | Формула Тейлора для функций нескольких переменных с дополнительным членом в форме Лагранжа и Пеано. Формула конечных приращений и следствия из нее. | [2,т.2 ] С.4-12 | [2,т.2 ] С.4-12 | ||
| 67. | Экстремум функции n переменных. Необходимое условие экстремума в терминах первого дифференциала. Достаточные условия строгого экстремума. Условие, достаточное для отсутствия экстремума в точке. | [2,т.2 ] С.18-25 | [2,т.2 ] С.18-25 | ||
| 68. | Неявные функции. Теорема о неявных функциях, определяемых одним уравнением (без доказательства). Вычисление производных неявных функций, определяемых системой уравнений. Якобиан системы функций. Вычисление производных неявных функций, определяемых из системы уравнений. | [2,т.2 ] С.26-31 | [2,т.2 ] С.26-31 | ||
| 69. | Отображения из Е в Е. Предел отображения, непрерывность отображения. Отображения, дифференцируемые в точке. Дифференциал отображения. Матрица производной отображения. Непрерывно дифференцируемые отображения. | [2,т.2 ] С.41-48 | [2,т.2 ] С.41-48 | ||
| 70. | Непрерывная дифференцируемость композиции отображений. Теорема об открытости образа открытого множества в случае непрерывно дифференцируемого отображения с неравным нулю якобианом. Теорема об обратном отображении. | [2,т.2 ] С.41-48 | [2,т.2 ] С.41-48 | ||
| 71. | Формулы замены переменных. Полярная замена. | [2,т.2 ] С.64-68 | [2,т.2 ] С.64-68 | ||
| 72. | Условный экстремум. Метод неопределенных множителей Лагранжа. | [2,т.2 ] С.74-85 | [2,т.2 ] С.74-85 | ||
| 73. | Понятие интеграла, зависящего от параметра. Собственные интегралы, зависящие от параметра. Непрерывность, дифференцирование и интегрирование по параметру. | [3,т.2 ] С. 138-148 | [3,т.2 ] С. 138-148 | ||
| 74. | Несобственные интегралы, зависящие от параметра. Равномерная сходимость. Критерий Коши равномерной сходимости. Признаки Вейерштрасса, Дирихле и Абеля равномерной сходимости несобственных интегралов, зависящих от параметра. | [3,т.2 ] С. 148-154 | [3,т.2 ] С. 148-154 | ||
| 75. | Теорема о предельном переходе под знаком интеграла. Непрерывность интеграла по параметру. | [3,т.2 ] С.154-157 | [3,т.2 ] С.154-157 | ||
| 76. | Теорема об интегрируемости несобственного интеграла, зависящего от параметра. Теорема о дифференцируемости несобственного интеграла по параметру. Несобственные интегралы от неограниченных функций. | [3,т.2 ] С. 157-167 | [3,т.2 ] С. 157-167 | ||
| 77. | Вычисление интегралов Дирихле и Пуассона. | [3,т.2 ] С. 161-167 | [3,т.2 ] С. 161-167 | ||
| 78. | Гамма-функция Эйлера и ее основные свойства. | [3,т.2 ] С. 167-169 | [3,т.2 ] С. 167-169 | ||
| 79. | Бета-функция Эйлера и ее основные свойства. | [3,т.2 ] С. 170-175 | [3,т.2 ] С. 170-175 | ЭКЗАМЕН | |
| 80. | Простейшие сведения о кривых. Определение простой непрерывной кривой. Направление на кривой. Длина дуги кривой. Длина дуги в роли параметра, натуральное представление кривой. Особые точки на кривой, гладкие кривые. Положительное направление касательной на кривой. | [2,т.2 ] С. 131-142 | [2,т.2 ] С. 131-142 | ||
| 81. | Криволинейные интегралы 1-го рода. Определение и формула для вычисления. Свойства интегралов 1-го рода. | [2,т.2 ] С.132-136 | [2,т.2 ] С.132-136 | ||
| 82. | Криволинейные интегралы 2-го рода. Определения и свойства. Лемма о хордах. Вычисление интегралов 2-го рода. Частные случаи, обобщения. Связь криволинейных интегралов 1-го и 2-го родов | [2,т.2 ] С.136-143 | [2,т.2 ] С.136-143 | ||
| 83. | Условие независимости криволинейного интеграла 2-го рода от пути интегрирования. | [2,т.2 ] С151-160 | [2,т.2 ] С151-160 | ||
| 84. | Квадрируемые множества на плоскости. Множества площади нуль. Критерий квадрируемости. | [2,т.2 ] С.85-92 | [2,т.2 ] С.85-92 | ||
| 85. | Квадрируемость фигуры, граница которой состоит из одной или нескольких спрямляемых кривых. Некоторые свойства меры Жордана. | [2,т.2 ] С.92-96 | [2,т.2 ] С.92-96 | ||
| 86. | Определение и условия существования двойного интеграла по прямоугольной области. Интегрируемость непрерывной функции. Ослабление условий интегрируемости. Определение и условия существования двойного интеграла в случае произвольной квадрируемой области. Лемма о пределах интегральных сумм специального вида. | [3,т.2 ] С. 237-242 | [3,т.2 ] С. 237-242 | ||
| 87. | Определение двойного интеграла при помощи произвольных разбиений области. Эквивалентность определений интегрируемости. Основные свойства двойного интеграла. | [3,т.2 ] С. 237-246 | [3,т.2 ] С. 237-246 | ||
| 88. | Сведение двойного интеграла к повторному. Случай прямоугольной области и произвольной квадрируемой области. Примеры вычисления двойного интеграла. | [2,т.2 ] С.105-111 | [2,т.2 ] С.105-111 | ||
| 89. | Формула Грина. Вычисление площадей плоских фигур с использованием криволинейных интегралов. | [2,т.2 ] С.143-147 | [2,т.2 ] С.143-147 | ||
| 90. | Критерий полного дифференциала в односвязной области. Восстановление функции по ее дифференциалу. | [2,т.2 ] С.143-147 | [2,т.2 ] С.143-147 | ||
| 91. | Тройные и n-кратные интегралы. Определение и основные свойства. Сведение кратных интегралов к повторным. | [2,т.2 ] С.94-105, С. 111-112 | [2,т.2 ] С.94-105, С. 111-112 | ||
| 92. | Свойства биективных непрерывно дифференцируемых отображений с необращающимся в нуль якобианом. Преобразование гладких кривых и контуров. Криволинейные координаты. Формула для площади образа области. Геометрический смысл знака якобиана. Геометрический смысл модуля якобиана. Замена переменных в двойном интеграле. Замена переменных в n-кратном интеграле. | [2,т.2 ] С.112-132 | [2,т.2 ] С.112-132 | ||
| Вычисление объемов. Полярные, сферические, цилиндрические координаты. Примеры замены переменных. Вычисление интеграла Пуассона. | [3,т.2 ] С. 334-339 | [3,т.2 ] С. 334-339 | |||
| Элементы теории поверхностей. Носитель поверхности, точка поверхности. Координатные линии на поверхности. Понятие кратной точки поверхности. Касательная к координатным линиям. Особые точки поверхности. Гладкие поверхности. Касательная плоскость к поверхности, нормальный вектор, нормальная прямая. Поверхности, задаваемые неявно. Уравнение касательной плоскости и нормального вектора. Понятие о поверхности уровня функции. Ортогональность градиента к поверхности уровня. | [2,т.2 ] С.267-274 | [2,т.2 ] С.267-274 | |||
| Понятие площади поверхности. Формула для вычисления площади поверхности. | [2,т.2 ] С.194-197 | [2,т.2 ] С.194-197 | |||
| Ориентация поверхности, односторонние и двусторонние поверхности. Кусочно-гладкие поверхности и их ориентация. | [2,т.2 ] С.197-205 | [2,т.2 ] С.197-205 | |||
| Определение и существование поверхностных интегралов 1-го и 2-го родов. Свойства поверхностных интегралов, примеры их вычисления. Поверхностные интегралы как пределы интегральных сумм. Интегралы по кусочно-гладким поверхностям. | [2,т.2 ] С.205-214 | [2,т.2 ] С.205-214 | |||
| Формула Гаусса-Остроградского: формулировка основной теоремы, доказательство формулы для специального класса областей. Выражение объема области через поверхностный интеграл. Многомерная формула интегрирования по частям. | [2,т.2 ] С.219-227 | [2,т.2 ] С.219-227 | |||
| Понятие векторного поля. Дифференцируемые векторные поля. Дивергенция и ротор векторного поля. Интерпретация формулы Гаусса-Остроградского в терминах теории поля. | [2,т.2 ] С.214-218, С. 227-231 | [2,т.2 ] С.214-218, С. 227-231 | |||
| Формула Стокса. | [2,т.2 ] С.227-236 | [2,т.2 ] С.227-236 | |||
| Определение последовательности областей, монотонно исчерпывающей данную область. Определение несобственного интеграла. Теорема о необходимом и достаточном условии сходимости несобственного интеграла от неотрицательной функции. Пример вычисления несобственного интеграла. | [2,т.2 ] С. 161-168 | [2,т.2 ] С. 161-168 | |||
Общий признак сравнения для несобственных интегралов. Стандартные функции сравнения 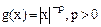 . Кратные несобственные интегралы в смысле главного значения. . Кратные несобственные интегралы в смысле главного значения.
| [2,т.2 ] С. 161-171 | [2,т.2 ] С. 161-171 | |||
| Определение функции с ограниченным изменением. Случай конечного промежутка и случай бесконечного промежутка. Классы функций с ограниченным изменением. Свойства функций с ограниченным изменением. Свойства функций с ограниченным изменением. Критерий для функций с ограниченным изменением (теорема 1, теорема 2). | [5,т.3 ] С. 74--88 | [5,т.3 ] С. 74--88 | |||
Интеграл Стилтьеса. Определение интеграла Стилтьеса. Общие условия существования интеграла Стилтьеса. Существование интеграла 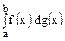 в случае, когда f(x) непрерывна, а g(x) имеет ограниченное изменение. Существование интеграла Стилтьеса в случае, когда f(x) интегрируема по Риману а g(x) липшицева. Вычисление интеграла Стилтьеса в случае, когда g(x) является пе в случае, когда f(x) непрерывна, а g(x) имеет ограниченное изменение. Существование интеграла Стилтьеса в случае, когда f(x) интегрируема по Риману а g(x) липшицева. Вычисление интеграла Стилтьеса в случае, когда g(x) является пе
Поиск по сайту©2015-2025 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2019-04-29 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |