Уравнения с разделяющимися переменными - это уравнение, правая часть которого f(x,y) есть произведение двух сомножителей f(x) и g(y), каждый из которых зависит только от одной переменной
y¢ =f(x)∙g(y). (12.10)
Уравнения с разделяющимися переменными интегрируются следующим образом: y¢ заменяется на 
, затем решают пропорцию, перенося к интегралам соответствующие функции. Получим:
(12.11)
Дифференциалы переменных x и y, и соответствующие функции стоят отдельно, т.е переменные отделены.
Если обозначить G(y) = 
, F(x) = 
, то уравнение (12.11) можно переписать в виде
dG(y) = dF(x).
Так как из равенства дифференциалов двух функций следует, что сами функции отличаются на произвольное постоянное слагаемое, то
G(y) = F(x) + C
или
= 
f(x)dx + C. (12.12)
Выражение (12.12) представляет собой общий интеграл уравнения (12.10). Вычислив интегралы в (12.12), получим решение исходного уравнения
Пример 2. Решить уравнение xy¢+ y = 0.
Решение. Разрешим уравнение относительно y¢: 
Здесь f(x) = -1/х, а g(y) = y.
Заменим в этом уравнении y¢ на dy/dx и решим пропорцию:
Получили уравнение с разделенными переменными. Интегрируя, находим
,
где C1 - произвольная постоянная. Отсюда следует: ln ½y½ = - ln½x½ + C1.
В данном случае удобно вместо C1 написать ln C2 (C2 > 0).
Тогда ln ½y½ = - ln ½x½ + ln C2
или
Так как ±C2 принимает любые значения, то обозначая ±C2 = C, окончательно получим
где C - произвольная постоянная.
Эта формула и дает общее решение заданного уравнения. Найдем теперь частное решение, удовлетворяющее начальному условию y½x=4 = 1/2. Для этого в равенство y = C/х подставим вместо x и y значения 4 и 1/2. Получим 
. Отсюда следует, что C = 2. Таким образом, искомое частное решение имеет вид 
.
Линейным однородным дифференциальным уравнение м первого порядка называется уравнение, правая часть которого однородна по переменным х и у, т.е. правая часть зависит только от отношения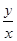 
.
. (12.13)
Обязательная замена переменных 
позволяет свести уравнение к уравнению с разделяющимися переменными. Подставим замену в уравнение
.
Раскроем скобки по правилу производной произведения. Тогда
Приведем уравнение к виду, разрешенному относительно 
.
Заменяем производную на отношение двух дифференциалов и решаем пропорцию
И интегрируем
.
Пример. Решить уравнение 
.
Решение. 
. Подставляем в уравнение
Вычисляем производную произведения
или, сокращая t, 
. Заменяем производную на отношение дифференциалов, решаем пропорцию и интегрируем
Заменяя 
, получим ответ 
Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно искомой функции y(x) и ее производной y¢(x). В общем случае оно имеет вид
y ¢ + p (x) y = f (x). (12.14)
Если f (x) º 0, то уравнение называется линейным уравнением без свободного члена (правой части) или линейным однородным уравнением. Итак,
y¢ + p (x)y = 0
линейное однородное уравнение (оно же уравнение с разделяющимися переменными).
Если f (x) ¹0, то уравнение (12.14) называется линейным неоднородным уравнением.
Например, уравнение
y ¢ - y cos2 x = х 2
является линейным неоднородным уравнением. Однородное по отношению к нему будет уравнение y ¢ - y cos2x = 0. Уравнение (12.14) можно интегрировать разными методами. Мы рассмотрим метод Бернулли. Он состоит в следующем. В уравнении (12.14) делаем замену:
y = u (х) ∙ v (х), (12.15)
Дифференцируя по правилу «производная произведения двух функций», имеем
y¢ = u¢(х) ∙ v(х) + u(х) ∙v¢(х) (12.16)
Подставим в уравнение (12.14) вместо y и y ¢ их выражения из (12.15) и (12.16), получим
u¢(х)v(х) + u(х)v¢(х) + p(х)u(х)v(х) = f(х)
или
u¢v + u ∙ (v¢ + p(x)v) = f(х). (12.17)
Так как одну из функций в (12.15) можно выбрать произвольно, то функцию v выберем таким образом, чтобы коэффициент при u обратился в нуль, т.е.
v¢ + p(x)v = 0. (12.18)
Тогда для функции u остается уравнение
u¢v = f(х). (12.19)
Уравнение (12.18) относительно функции v(x) является уравнением с разделяющимися переменными. Поэтому из (12.18) имеем:
Интегрируя, находим
Так как функция v - это любая функция, удовлетворяющая (12.18), то полагаем C=0. Итак,
ln(v) = - 
pdx Þ 
.
Представляя найденную функцию v(x) в уравнение (12.19), получим
Отсюда следует
Интегрируя, получим
(12.20)
где C - произвольная постоянная. Для того, чтобы найти y(x), умножим найденную u(x) на v(x):
(12.21)
Формула (12.21) дает общее решение дифференциального уравнения (12.14).
Пример. Найти общее решение уравнения
Решение. Это линейное неоднородное уравнение, где
Выполнив замену y = u∙v, получаем y¢ = u¢∙v + u∙v¢.
Заданное дифференциальное уравнение перепишем в виде
или
Приравняем выражение в скобках нулю:
Получили уравнение для функции v(x) - уравнение с разделяющимися переменными. Интегрируем его:
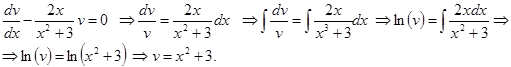
Подставляя функцию v(x) в уравнение, найдем уравнение для функции u(x):
u¢(x2 + 3) = (x2 + 3)cosx.
Отсюда следует
u¢ = cos(x) или u = 
cos(x) dx + C Þ u = sin(x) + C.
Теперь находим общее решение заданного уравнения y(x):
y = uv Þ y = (sin(x) + C)(x2 + 3).