Учебный модуль 6. Дифференциальные уравнения. Тема 13. Линейные дифференциальные уравнения второго порядка.
ЛЕКЦИЯ 13. Основные понятия теории дифференциальных уравнений второго порядка. Линейные дифференциальные уравнения второго порядка. Уравнения второго порядка с постоянными коэффициентами.
Дифференциальное уравнение второго порядка - это уравнение, в которое входят независимая переменная x, неизвестная функция y (x), первая y’ (x) и вторая y’’ (x) производные неизвестной функции. Общий вид дифференциального уравнения второго порядка
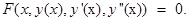(13.1)
Здесь F - заданная функция четырех аргументов 
. Она может не зависеть от x, y и y’(или от двух или трех переменных), но должна обязательно содержать y ’’(х).
Если уравнение (13.1) решить относительно y ’’, то получим разрешенный вид
y’’( х) = f (x, y, y ’) (13.2)
где f - заданная функция трех аргументов x, y (х) и y ’(х). В дальнейшем мы будем рассматривать только уравнения в разрешенном виде.
Решение дифференциального уравнения (13.2) - это функция 
, которая, при подставке в уравнение, обращает его в тождество (тождество справедливо при любых значениях х):
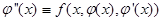(13.3)
Общим решением уравнения второго порядка называется функция, содержащая две произвольные постоянные C1 и C2
, (13.4)
которая при любых значениях постоянных C1 и C2 является решением уравнения.
Если заданы начальные условия (это называется задача Коши) 
, где 
и 
числа, то, подставляя начальные условия в общее решение, получим систему двух уравнений из которой находим конкретные значения постоянных C1 и C2
Такое решение будет называться частным решением, удовлетворяющим данным начальным условиям.
Теорема существования и единственности решения дифференциального уравнения второго порядка.
Если правая часть уравнения f (x, y, y ’) непрерывна в некоторой области D как функция трех переменных и имеет непрерывные частные производные по аргументам у и у ’, т.е.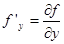 
и 
, то каждой паре начальных условий соответствует единственное частное решение.
Определение. Линейным неоднородным дифференциальным уравнением второго порядка называется уравнение вида
, (13.5)
где p (x), q (x) – коэффициенты, а f (x) – правая часть уравнения.
Если f (x) =0, то уравнение называется однородным
(13.6)
Определение. Функции у 1(х) и у 2(х) называются линейно независимыми на некотором промежутке, если их отношение не равно числу
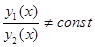или 
(13.7)
и линейно зависимыми, если 
или 
. Например, линейно независимы 
и 
или 
и 
, а линейно зависимы и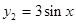 
Теорема. Есл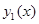и 
и 
частные решения уравнения , то их линейная комбинация
(13.8)
тоже есть решение этого уравнения (С1 и С2 – постоянные величины).
Доказательство. Возьмем первую и вторую производные от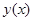 
и подставим в левую часть уравнения (13.6) (учли, что постоянный множитель можно выносить за знак производной) и покажем, что получим тождественный ноль
Тогда
раскрывая скобки и приводя подобные члены, получим
Действительно, 
, так как 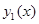решение уравнения. По этой же причине тождественно нулю и выражение 
.
Определение. Вронскианом или определителем Вронского 
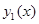для дифференцируемых функций и называется определитель вида
. (13.9)
Теорема. Если функции 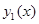и линейно зависимы, т. е. , то Вронскиан для этих функций равен нулю. Действительно, так как 
, то
.
Можно доказать, что обратное не верно, из равенства нулю Вронскиана не следует линейная независимость функций.
Теорема. Если функции 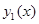и линейно независимые решения уравнения (13.6), то Вронскиан для них не будет равен нулю.
Замечание. Функция 
отвечает нулевым начальным условиям и называется тривиальным решением дифференциального однородного уравнения (13.6). По теореме единственности решения, это единственное решение, удовлетворяющее нулевым условиям. Такое решение линейно зависимо от любого другого, так как константа С просто обращается в ноль 
. Тривиальное решение мы не рассматриваем.
Доказательство. Подставим 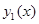и в уравнение (13.6) и составим систему.
Умножим первое уравнение на 
, а второе на 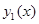и вычтем из первого второе уравнение, приведя подобные члены
Тогда
(13.10)
Так как при 
стоит Вронскиан
,
а первое выражение есть производная от Вронскиана со знаком минус
то уравнение (13.10) можно переписать в виде
Получили для Вронскиана дифференциальное уравнение первого порядка с разделяющимися переменными. Схема решения такого уравнения известна. Заменяем 
на отношение двух дифференциалов и разделяем переменные
Интегрируем
. (13.11)
Или 
. Правая часть равенства величина строго положительная еf ( x ) > 0 для любого показателя f (x). Отсюда следует, что 
. Если убрать модуль у 
, то (13.11) можно записать в виде
, где 
(13.12)
Следствие. Формула Лиувилля. Так как 
, то в (13.12) можно сделать подстановку
(13.13)
Поделим (13.13) на 
и вспомним формулу производной частного двух функций, в нашем случае 
Проинтегрируем полученное выражение, учитывая, что 
.
или
Взяв С = 1 и С1 = 0, получим, что второе линейно независимое решение можно найти, если известно первое независимое решение
(13.14)
Эти и есть формула Лиувилля.
Теорема об общем решении линейного однородного дифференциального уравнения. Пусть 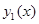и линейно независимые решения однородного уравнения (13.6). Тогда их линейная комбинация 
будет общим решением уравнения (13.6).
Доказательство. То, что линейная комбинация решений тоже есть решение, мы доказали ранее. Покажем теперь, что для любой пары начальных условий 
существует единственная пара постоянных С 1 и С 2, такая что решение 
удовлетворяет данным начальным условиям (это значит, что каждой паре начальных условий соответствует единственное частное решение). Для этого возьмем производную 
и подставим начальные условия
В этой системе 
числа, так как это известные функции вычисленные в известной точке. С 1 и С 2 неизвестные величины. Система имеет единственное решение, если ее главный определитель не равен нулю Проверим, что это так.
Определитель системы это Вронскиан вычисленный в точке 
, а он не равен нулю.
Теорема об общем решении линейного неоднородного дифференциального уравнения 
.
Общим решением неоднородного линейного уравнения будет сумма трех функций
, (13.15)
где 
и 
линейно независимые решения однородного уравнения (13.6), линейная комбинация 
общее решение однородного уравнения, а 
частное решение неоднородного уравнения
Доказательство. Докажем, что выражение (13.15) является решением. Возьмем первую и вторую производную, подставим в левую часть уравнения и получим, что это выражение тождественно равно 
.
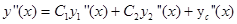
Тогда
раскроем скобки и приведем подобные члены
и 
так как 
и 
решения однородного уравнения. А есть решение неодногодного уравнения, оно дает тождественное равенство 
.
Покажем теперь, что для любой пары начальных условий 
существует единственная пара постоянных С 1 и С 2, такая что решение 
удовлетворяет данным начальным условиям (это значит, что каждой паре начальных условий соответствует единственное частное решение). Для этого возьмем производную и подставим ее в начальные условия
В этой системе 
числа, так как это известные функции вычисленные в известной точке. С 1 и С 2 неизвестные величины.
Приведем систему к стандартному виду, перенеся числа 
налево
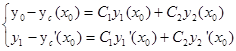
Система имеет единственное решение, если ее главный определитель не равен нулю. Проверим, что это так.
Для неоднородного уравнения определитель системы совпадает с определителем для однородного уравнения.