Пусть дан набор из n функций  , зависящих от независимой переменной х. Нормальной системой дифференциальных уравнений первого порядка назовем систему
, зависящих от независимой переменной х. Нормальной системой дифференциальных уравнений первого порядка назовем систему  дифференциальных уравнений вида
дифференциальных уравнений вида
 (14.1)
(14.1)
В нормальной системе правые части уравнений  не содержат производных искомых функций. Решением системы (14.1) называется совокупность функций
не содержат производных искомых функций. Решением системы (14.1) называется совокупность функций  удовлетворяющих каждому из уравнений этой системы.
удовлетворяющих каждому из уравнений этой системы.
Системы уравнений второго, третьего и более высоких порядков можно свести к нормальной системе, если ввести новые функции, заменяя ими производные  и т. д. например, систему
и т. д. например, систему

можно свести к четырем уравнениям первого порядка заменой 


Для нормальной системы дифференциальных уравнений теорема существования и единственности решения формулируется следующим образом. Пусть в некоторой области G правые части уравнений системы (14.1) 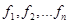 непрерывны по всем переменным и имеют в ней непрерывные частные производные по переменным
непрерывны по всем переменным и имеют в ней непрерывные частные производные по переменным  . Тогда каждому набору начальных условий
. Тогда каждому набору начальных условий  , где
, где  числа. отвечает единственное частное решение системы (14.1).
числа. отвечает единственное частное решение системы (14.1).
Любую нормальную систему можно свести к одному уравнения порядка n. Но проще всего показать этот алгоритм на линейных системах.
Нормальная система называется линейной, если правые части 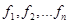 линейны по переменным
линейны по переменным  .
.

Рассмотрим систему двух линейных уравнений с постоянными коэффициентами
 (14.2)
(14.2)
Здесь  постоянные коэффициенты при неизвестных функциях
постоянные коэффициенты при неизвестных функциях  .
.
Систему (14.2) можно свести к одному дифференциальному уравнению второго порядка с постоянными коэффициентами. Для этого выделим первое уравнение и возьмем от него производную

Подставим  из второго уравнения системы
из второго уравнения системы

Раскроем скобки

Подставим  из первого уравнения системы
из первого уравнения системы
 (14.3)
(14.3)
и приведем подобные члены. Тогда получим уравнение второго порядка

Или, в стандартной форме
 (14.4)
(14.4)
Решив это уравнение, подставим у 1 в (14.3) и найдем у 2.
Если функции  равны нулю
равны нулю  , то система (14.2) называется однородной. Линейная однородная система двух дифференциальных уравнений первого порядка называется автономной.
, то система (14.2) называется однородной. Линейная однородная система двух дифференциальных уравнений первого порядка называется автономной.
 (14.5)
(14.5)
Замечание. Если неизвестные функции обозначены  и
и  , а
, а  независимая переменная, то автономная система сводится к однородному дифференциальному уравнению первого порядка, позволяющему найти зависимость
независимая переменная, то автономная система сводится к однородному дифференциальному уравнению первого порядка, позволяющему найти зависимость  . В этом случае
. В этом случае  и
и  координаты точки в момент времени
координаты точки в момент времени  , а производные имеют смысл проекций вектора скорости. В силу традиций вводятся обозначения
, а производные имеют смысл проекций вектора скорости. В силу традиций вводятся обозначения  ,
,  и система приобретает вид
и система приобретает вид

Если разделить второе уравнение на первое и учесть, что  , то получим однородное уравнение первого порядка
, то получим однородное уравнение первого порядка

Которое решается заменой  . Решение этого уравнения дает траекторию движения тела на плоскости
. Решение этого уравнения дает траекторию движения тела на плоскости  .
.
Пример 1. Найти общее решение системы

Дифференцируем первое уравнение  . Подставляем
. Подставляем  из второго уравнения системы
из второго уравнения системы  . Заменяем
. Заменяем  на его выражение из первого уравнения
на его выражение из первого уравнения  и подставляем в уравнение для
и подставляем в уравнение для  .
.

Решаем однородное уравнение второго порядка

Ищем решение уравнения в виде  тогда
тогда 
 . Получим характеристическое уравнение
. Получим характеристическое уравнение

Так как дискриминант равен нулю, то корни характеристического уравнения вещественные равные  . Общее решение дифференциального уравнения имеет вид
. Общее решение дифференциального уравнения имеет вид

Решаем неоднородное уравнение  , ищем частное решение в виде
, ищем частное решение в виде  . Берем первую и вторую производные и подставляем в уравнение
. Берем первую и вторую производные и подставляем в уравнение 

Отсюда, сравнивая левую и правую части, получим 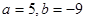 .
.

Теперь найдем  . Для этого вычислим
. Для этого вычислим 

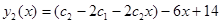
Общее решение системы имеет вид

Пример 2: Найти общее решение системы (здесь независимая переменная t, а функции  )
)

Дифференцируя по  первое уравнение, получим
первое уравнение, получим

Подставим сюда  из второго уравнения, тогда
из второго уравнения, тогда

Из первого уравнения системы находим y  и подставляем в уравнение для
и подставляем в уравнение для  .
.
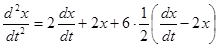
Приводя подобные слагаемые в последнем уравнении, получаем линейное однородное дифференциальное уравнение второго порядка относительно  :
:

Характеристическое уравнение имеет вид  , а его решения
, а его решения  ,
,  .
.
Тогда общим решение дифференциального уравнения будет  .
.
Зная х, найдем у
 и
и 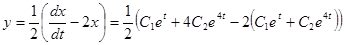
Решение данной системы имеет вид:
 .
.
Линейные системы можно решить и матричным методом. Покажем матричный метод решения на примере автономной системы (14.5).

Автономная система характеризуется тремя матрицами. Матрицей коэффициентов А, матрицей-столбцом (вектором) неизвестных Х, матрицей-столбцом (вектором) производных Х’



В матричной форме систему можно записать, используя произведение матриц

Будем искать решение системы в виде вектора  , где
, где  , а
, а  . Неизвестные функции
. Неизвестные функции  и
и  одинаково зависят от х, но имеют разные коэффициенты при
одинаково зависят от х, но имеют разные коэффициенты при  . Тогда вектор производных будет равен
. Тогда вектор производных будет равен  . Систему можно записать в виде
. Систему можно записать в виде

Так как  , то на него можно сократить и привести подобные члены. Получим обычную линейную систему двух уравнений с двумя неизвестными
, то на него можно сократить и привести подобные члены. Получим обычную линейную систему двух уравнений с двумя неизвестными 
 (14.6)
(14.6)
Из этой системы надо найти три неизвестных  . Если определитель системы не равен нулю
. Если определитель системы не равен нулю

то система имеет единственное тривиальное решение  или
или  . Такое решение очевидно и не имеет практического смысла. Система имеет не нулевое решение только в том случае, если определитель равен нулю, но такой решение не будет единственным.
. Такое решение очевидно и не имеет практического смысла. Система имеет не нулевое решение только в том случае, если определитель равен нулю, но такой решение не будет единственным.

Если раскрыть скобки и привести подобные члены, то получим уравнение
 (14.7)
(14.7)
Это уравнение называется характеристическим и в точности совпадает с левой частью уравнения (14.4).
Если к орни характеристического уравнения действительные и различные  , то подставим по очереди каждый из корней в систему (14.6) и найдем решение, дающее зависимость
, то подставим по очереди каждый из корней в систему (14.6) и найдем решение, дающее зависимость  от
от  для каждого значения k. Подставив эти значения в искомые функции
для каждого значения k. Подставив эти значения в искомые функции  и
и  , найдем два вектора решений.
, найдем два вектора решений.
Для 
 ,
, 
Для 
 ,
, 
(здесь «2» номер решения, а не возведение в квадрат)
Общее решение уравнения 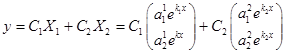 или
или
 , ,
|
где  - произвольные постоянные.
- произвольные постоянные.
Пример 3. Найти общее решение системы маричным методом:

Матрица  . Система (14.6)
. Система (14.6)
 (14.8)
(14.8)
Составим характеристическое уравнение (14.7)
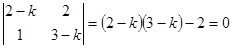
или 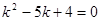 . Его решения имеют вид
. Его решения имеют вид  ,
, 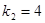 .
.
Подставим  в систему (14.8) и найдем
в систему (14.8) и найдем  :
:
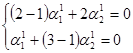 .
.
или
 .
.
Откуда  . Возьмем
. Возьмем  , тогда
, тогда  (
( можно брать равным любому числу,
можно брать равным любому числу, 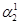 выражается через него. Получили решение системы
выражается через него. Получили решение системы  или
или 
Замечание. Можно было взять  , тогда
, тогда  .
.  . Ответы находятся с точностью до постоянного множителя).
. Ответы находятся с точностью до постоянного множителя).
Аналогично, подставим 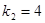 в систему (14.8)
в систему (14.8)

и определяем  :
:
 .
.
Тогда  и
и  . Получаем второе решение системы:
. Получаем второе решение системы:  .
. 
Общее решение системы 
 или
или 
.
Если корни характеристического уравнения (14.7) комплексные, то это обязательно два комплексно - сопряженных числа

|
Этим корням будут соответствовать решения


|
Коэффициенты  и
и  определяются из системы уравнений (14.8) и ответ выглядит точно также. Но если мы не хотим работать с комплексными числами, то используем формулы Эйлера. Получим
определяются из системы уравнений (14.8) и ответ выглядит точно также. Но если мы не хотим работать с комплексными числами, то используем формулы Эйлера. Получим

 , ,
|
где  и
и  - вещественные числа, определяемые через
- вещественные числа, определяемые через  и
и  .
.
Ответ будет иметь вид
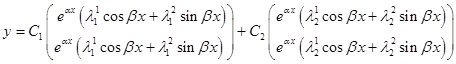
Пример 4:
Найти общее решение системы (здесь неизвестные функции  и
и  , а
, а  независимая переменная).
независимая переменная).

Составим характеристическое уравнение:

или  .
.
Его решения имеют вид  ,
,  .
.
Составляем систему (14.8) для корня  и определяем
и определяем  :
:
 .
.
или
 .
.
Находим коэффициенты  :
:
 ,
,  .
.
Записываем решение (12):
 .
.
Подставляя  в систему (14.8), находим
в систему (14.8), находим  ,
,  .
.
 .
.
Перепишем решения, используя формулу Эйлера  ,
,  .
.


За системы частных решений можно взять отдельно вещественные и мнимые части:


Общим решением представленной системы будет:
