Проблема измерения полезности одна из самых сложных в экономической теории. Ввиду того, что понимание полезности весьма индивидуально, психологично, неустойчиво и относительно, измерить полезность впрямую представляется практически невозможным. В прошлом для удобства исследования экономисты пытались производить количественные оценки полезности и даже придумывали для этого специальные счетные единицы. Такой подход к измерению полезности получил название количественного (кардиналистского) подхода. Однако условность, абстрактность, субъективность количественных измерений были настолько очевидными, что от подобных попыток пришлось отказаться.
Сейчас больше говорят не об измерении, а об оценке полезности, а еще точнее — о сравнении полезностей, получаемых от потребления различных наборов благ. Действительно, если потребитель не может измерить полезность количественно, то он всегда может сравнить полученную полезность от потребления, скажем, двух наборов благ и сказать, что первый для него более полезен, чем второй. Этот подход называется порядковым (ординалистским), он считается основным при анализе поведения потребителя.
Не подлежит сомнению, что полезность зависит от количества и качества потребляемых благ. Любой набор благ (х1;...; хn), где х1;...;хn — количественные значения благ 1,..., n, называется потребительской корзиной. В дальнейшем будем считать, что потребитель извлекает полезность из потребления корзины, способен сравнивать ее с другими корзинами и ранжировать корзины по убыванию или возрастанию полезностей. Для оценки взаимосвязи полезностей и объемов потребления благ в микроэкономике используется аппарат функций полезности.
Функция полезности есть целевая функция модели потребительского выбора. Она представляет собой зависимость максимально возможного уровня полезности от потребления определенного количества благ: U =f(x1,..., хn), где х1;...;хn — объемы потребления благ 1,..., n.
Сторонники количественного подхода к анализу полезности — видные экономисты XIX века У. Джевонс, К. Менгер, Л. Вальрас и другие предлагали для удобства исследования спроса измерять общую полезность от потребления блага в неких количественных показателях. Подобно тому, как энергетическая ценность продуктов питания измеряется в калориях, были предложены специальные единицы для измерения полезности — «ютили». Например, потребление одного стакана молока приносит потребителю 10 ютиль и т.д. Количественной школе принадлежат большие достижения в теории потребления, среди которых — открытие предельной полезности и закона ее убывания, обоснование равновесия потребителя на основе эквимаржинального принципа, исследование психолого-экономических законов потребления и др.
Предельная полезность — это дополнительная полезность, полученная за счет увеличения потребления данного блага на одну единицу. или же — частная производная функции полезности по объему потребления i-го блага:
MU(xi) = ΔU/Δхi ≈ U′(хi).
При фиксированных объемах потребления всех прочих благ зависимость общей и предельной полезности от потребления i-го блага показана на рис. 3.1.
Отрезок ОС показывает полезность фиксированной потребительской корзины при нулевом потреблении i-го блага. Длина отрезка OD равна тангенсу угла наклона касательной графику функции полезности U в точке А. Из графика а видно, что угол наклона касательных убывает с ростом хi значит MU(xi) тоже убывает. Если MU(xi) < 0, то прирост потребления блага приводит к сокращению полезности.
Принцип убывающей предельной полезности называется первым законом Госсена. Он говорит о том, что с ростом потребления какого-либо одного блага при фиксированном объеме потребления всех остальных благ общая полезность возрастает убывающими темпами, а предельная полезность при этом убывает. Математически это означает, что MU(x) = U'(x) > 0; MU'(x) = U"(x) < 0.

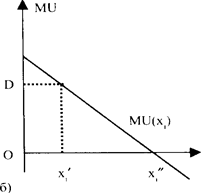
Рис. 3.1. Общая и предельная полезность, первый закон Госсена
По Госсену, убывание предельной полезности понимается двояко. С одной стороны, при однократном потреблении нескольких долей одного блага полезность каждой дополнительной доли сокращается. С другой стороны, при многократном последовательном потреблении того же блага каждый новый акт потребления приносит потребителю все меньше и меньше полезности.
Предположим теперь, что блага 1,..., n имеют рыночные цены Р1,..., Рn. Если потребитель располагает фиксированным бюджетом (доходом в единицу времени) — I, то задача оптимизации полезности сводится к такому распределению бюджета между благами, чтобы общая полезность от купленного набора была бы наибольшей. Оптимум потребителя достигается, когда:
а) средства распределены таким образом, что для всех купленных товаров имеет место равенство:
МU(хi) / Р1 = MU(x2) / P2 =... = MU(xn) / Pn = λ, где λ - величина, характеризующая предельную полезность денег.
б) для всех некупленных товаров MU(xm) / Pm ≤ λ.
Утверждение а) называется вторым законом Госсена. Оно утверждает, что при оптимуме потребителя уровень полезности, получаемой от расходования последней денежной единицы, одинаков для всех покупаемых товаров. В этом и состоит смысл эквимаржинального принципа.
Этим законом доказывается также обратная зависимость спроса на товар и рыночной цены. Очевидно, что если рыночная цена i-ro блага растет, то для восстановления исходного равенства (а) потребитель должен сокращать его потребление и увеличивать таким образом предельную полезность.