Занятие 29-30 Понятие дифференциального уравнения. Виды ДУ.
Задание:
1) Внимательно изучи теоретический материал.
2) Закончи предложения:
| Дифференциальное уравнение - это … |
| Порядок дифференциального уравнения - это … |
| ОДУ первого порядка - это … |
| Решение ДУ первого порядка - это … |
| Общее решение ДУ первого порядка - это … |
| Интегральная кривая ДУ - это … |
| Типы ОДУ первого порядка: 1) 2) 3) 4) |
УСПЕХОВ!!!
Теоретический материал
Дифференциальным уравнением называется уравнение, связывающее независимые переменные, функцию этих переменных и производные (дифференциалы) этой функции.
Если независимая переменная одна, то уравнение называется обыкновенным (ОДУ); если независимых переменных две или больше, то уравнение называется дифференциальным уравнением в частных производных.
Наивысший порядок производной (дифференциала), входящей в уравнение, называется порядком дифференциального уравнения.
Примеры:
1) 
- ОДУ первого порядка;
2) 
- ОДУ второго порядка;
3) 
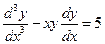- ОДУ третьего порядка;
4) 
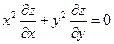- уравнение в частных производных первого порядка.
Мы будем рассматривать обыкновенные дифференциальные уравнения – ОДУ.
Задачи, приводящие к дифференциальным уравнениям
Дифференциальные уравнения имеют огромное прикладное значение. С помощью дифференциальных уравнений описываются многие реальные природные процессы. Они находят широкое применение в биологии, химии, экономике и многих других науках.
Примеры:
1) Движение тела в поле силы тяжести: тело массой m падает под действием силы тяжести mg, сила сопротивления 
. Пользуясь 2 законом Ньютона, составим ДУ
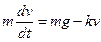, где ускорение тела 
2) Уравнение радиоактивного распада 
, k – постоянная распада, m – количество неразложившегося вещества в момент времени t
3) Уравнение движения тела массы m под влиянием силы F, зависящей от времени, положения тела х(t), и его скорости 
4) Закон размножения бактерий
Масса бактерий m зависит от времени 
5) Закон охлаждения тел 
, где T(t) – температура тела в момент времени t, k – коэффициент пропорциональности, t0 – температура воздуха.
6) Уравнение показательного роста и показательного убывания (рост численности населения в заданном регионе; убывание популяции некоторых животных; рост биомассы лишайников) 
7) Задача о свободных гармонических колебаниях тела массой m (движение поршня в цилиндре двигателя автомобиля, движение качелей, биение сердца)
,где 
- круговая частота
ОДУ первого порядка
Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида
или
Решением ДУ первого порядка называется такая дифференцируемая функция 
, которая при подстановке в уравнение обращает его в тождество.
Общим решением ДУ первого порядка называется такая дифференцируемая функция 
, которая при любом значении произвольной постоянной С является решением уравнения.
Если общее решение ДУ найдено в неявном виде, т.е. в виде уравнения Ф(х,у,С)=0, то такое решение называется общим интегралом ДУ.
Процесс отыскания решения ДУ называется интегрированием.
Примеры:
1) Проверить, что функция 
является решением уравнения 
Решение:
Найдем производную функции 
Подставим в уравнение 
2) Проверить, что неявно заданная функция у - 
является общим интегралом ДУ 
Решение:
Дифференцируем неявно заданную функцию 
Выразим 
Подставляем в уравнение 
График решения ДУ называется интегральной кривой ДУ. Общему решению ДУ соответствует семейство интегральных кривых.
Частным решением ДУ первого порядка называется функция 
, полученная из общего решения при конкретном значении постоянной С=С0.
Если общее решение найдено в неявном виде Ф(х,у,С)=0, то уравнение Ф(х,у,С0)=0 называется частным интегралом ДУ.
Геометрически, частное решение (частный интеграл Ф(х,у,С0)=0) – одна интегральная кривая, проходящая через точку (х0;у0).
Задачей Коши называется задача отыскания решения ДУ первого порядка, удовлетворяющего заданному начальному условию у(х0)=у0.
Типы ОДУ первого порядка
1) ОДУ с разделяющимися переменными
2) Однородные ОДУ
3) Уравнения в полных дифференциалах
4) Линейные ОДУ