ВВЕДЕНИЕ
При выполнении заочниками контрольных работ и подготовке к экзамену необходимо изучить теоретический материал, ориентируясь на программу курса, ознакомиться с решением примеров, приведенных в методических указаниях, прорешать контрольные задания.
Правила оформления и выполнения контрольных работ
При выполнении контрольных работ необходимо строго придерживаться указанных ниже правил.
1. Студент должен выполнять контрольные задания по варианту, в двойном номере которого вторая цифра совпадает с последней цифрой его шифра – номера его зачетной книжки.
2. Каждая контрольная работа должна быть выполнена в отдельной тетради в клеточку чернилами синего или черного цвета.
3. Образец оформления титульного листа (обложки) тетради можно посмотреть на выпускающей кафедре или на кафедре высшей математики.
4. В работу должны быть включены все задачи, указанные в задании. Работы, содержащие не все задачи задания, а также задачи не своего варианта, не рецензируются.
5. Задачи нужно решать в том порядке, в котором они указаны в контрольной работе.
6. Перед решением каждой задачи надо полностью выписать ее условие.
Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи (рисунки).
7. Компьютерное оформление работы не рецензируется.
8. Возвращенная прорецензированная незачтенная работа исправляется студентом; исправление записывается в конце работы. Вносить исправления в проверенный текст работы – запрещается.
ТЕОРЕТИЧЕСКИЙ И СПРАВОЧНЫЙ МАТЕРИАЛ
2.1.Комплексные числа
Комплексным числом называется число вида  , где , где  и и  действительные числа, а действительные числа, а 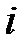 – мнимая единица такая, что – мнимая единица такая, что  .
При этом такая запись комплексного числа называется алгебраической; .
При этом такая запись комплексного числа называется алгебраической;  является действительной частью комплексного числа, а является действительной частью комплексного числа, а  – мнимою. Каждое комплексное число может быть так же представлено в тригонометрической форме: – мнимою. Каждое комплексное число может быть так же представлено в тригонометрической форме:  или показательной форме: или показательной форме:  , где , где 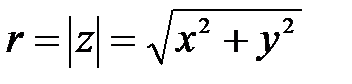 – модуль комплексного числа, а – модуль комплексного числа, а  – аргумент комплексного числа такой, что – аргумент комплексного числа такой, что  , где , где 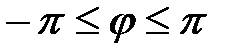 или или  .
Комплексные числа изображаются на комплексной плоскости. Для них введены операции сложения, умножения, вычитания и деления. Так же их можно возводить в степень и извлекать из них корень, для этого используют формулу Муавра. .
Комплексные числа изображаются на комплексной плоскости. Для них введены операции сложения, умножения, вычитания и деления. Так же их можно возводить в степень и извлекать из них корень, для этого используют формулу Муавра.
|
Пример выполнения задания № 1. Дано комплексное число  . Записать данное число в алгебраической форме (т.е. в форме
. Записать данное число в алгебраической форме (т.е. в форме  ).
).
Для этого умножаем знаменатель и числитель на сопряженное знаменателю выражение. Смотрим на формулу  . В знаменателе уже есть
. В знаменателе уже есть  , поэтому знаменатель и числитель нужно умножить на сопряженное выражение
, поэтому знаменатель и числитель нужно умножить на сопряженное выражение  , то есть на
, то есть на  :
:
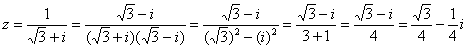
Представим в тригонометрической форме число 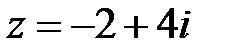 . Найдем модуль комплексного числа
. Найдем модуль комплексного числа 
то  - воспользуемся нечетностью арктангенса. К сожалению, в таблице отсутствует значение
- воспользуемся нечетностью арктангенса. К сожалению, в таблице отсутствует значение 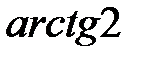 , поэтому в подобных случаях аргумент приходится оставлять в громоздком виде:
, поэтому в подобных случаях аргумент приходится оставлять в громоздком виде:
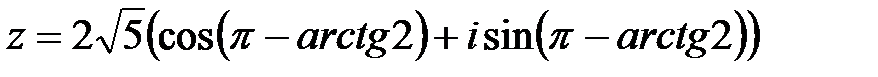 – число
– число  в тригонометрической форме.
в тригонометрической форме.
Элементы линейной алгебры
Пример выполнения задания № 2. Найти X из матричного уравнения
 .
.
Решение
Запишем уравнение в матричной форме 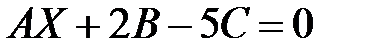 , где
, где
 ,
,  ,
,  , 0=
, 0=  .
.
Преобразуем уравнение 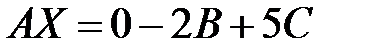 . Выполним действия с матрицами в правой части
. Выполним действия с матрицами в правой части
 .
.
Обозначим полученную матрицу  и запишем уравнение в виде
и запишем уравнение в виде
 .
.
Умножим обе части равенства слева на  , получим
, получим  .
.
С учетом того, что  , решением уравнения будет
, решением уравнения будет  ,
,
где  – матрица обратная матрице
– матрица обратная матрице 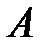 .
.
Если определитель матрицы  отличен от нуля, то она имеет обратную, которая имеет вид:
отличен от нуля, то она имеет обратную, которая имеет вид:
 ,
,
где  - определитель матрицы
- определитель матрицы 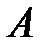 ,
,
 - алгебраическое дополнение элемента
- алгебраическое дополнение элемента  матрицы
матрицы  .
.
Для данной системы:
 ,
,
 ,
,  ,
, 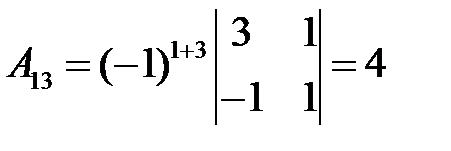 ,
,
 ,
,  ,
,  ,
,
 ,
,  ,
,  .
.
Таким образом,
 .
.
Найдем решение данного уравнения, умножив матрицу А -1 на матрицу  .
.
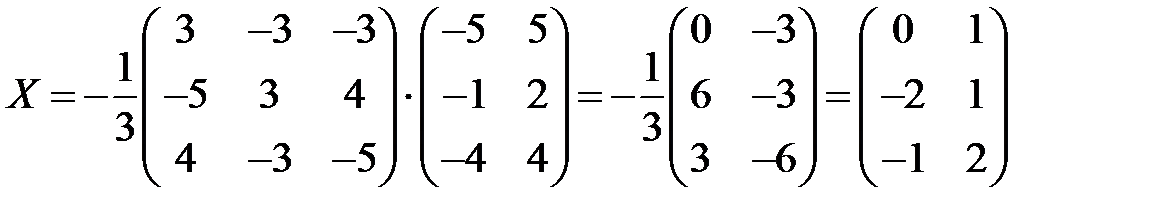 .
.
Проверим найденное решение, подставив его в исходное уравнение.

 .
.
 Итак, найденное значение
Итак, найденное значение  обращает уравнение в тождество.
обращает уравнение в тождество.
Ответ:  .
.
Пример выполнения задания № 3. Решить систему методом Крамера

Решение
Если  – главный определитель матрицы, составленный из коэффициентов при неизвестных системы, а
– главный определитель матрицы, составленный из коэффициентов при неизвестных системы, а  – вспомогательный определитель, полученный из главного заменой j –го столбца столбцом свободных членов, то при
– вспомогательный определитель, полученный из главного заменой j –го столбца столбцом свободных членов, то при  система имеет единственное решение, определяемое по формулам
система имеет единственное решение, определяемое по формулам 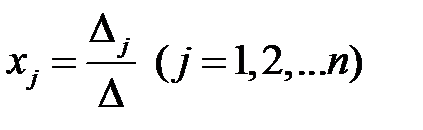 . Эти формулы называются формулами Крамера. Для нашей системы
. Эти формулы называются формулами Крамера. Для нашей системы
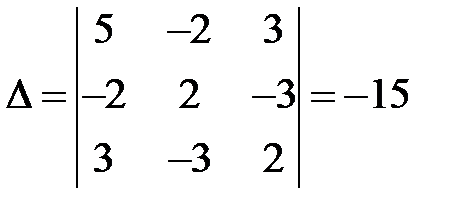 ;
;
 ;
;  ;
; 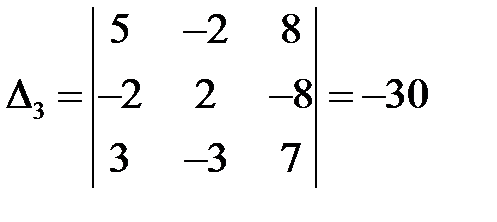 ;
;
 ;
;  ;
;  .
.
Решение системы (0; –1; 2).
Сделаем проверку, подставив найденные значения в систему
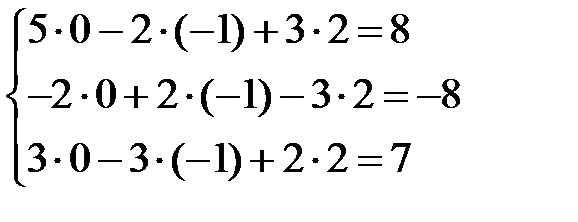


Итак, найденное решение обращает уравнения в верные равенства.
Ответ: (0; –1; 2).