Пример выполнения задания № 4. Найти угол между векторами  , если
, если 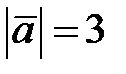 ,
, 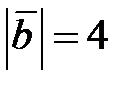 ,
,  ,
, 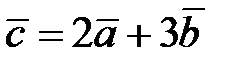 ,
,  .
.
Решение
Скалярным произведением двух векторов  называется число, равное произведению длин этих векторов на косинус угла между ними.
называется число, равное произведению длин этих векторов на косинус угла между ними.
 .
.
Из определения скалярного произведения
 .
.
Найдем  ,
,  ,
,  .
.
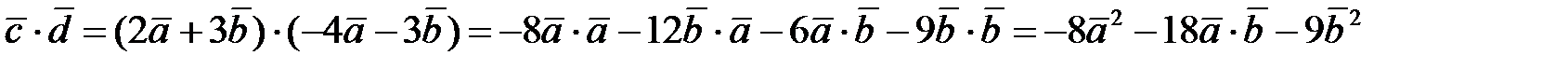 , где
, где
 ,
, 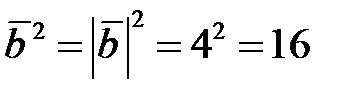 ,
, 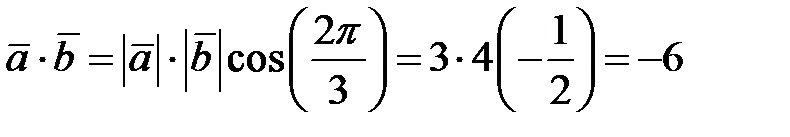 .
.
С учетом этого
 ,
,
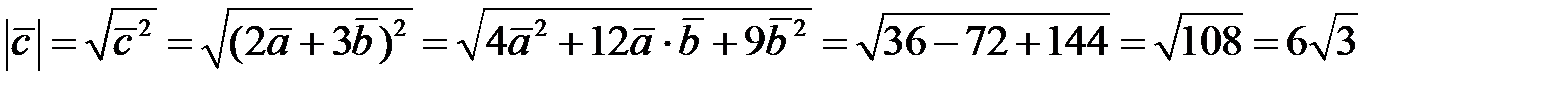 ,
,
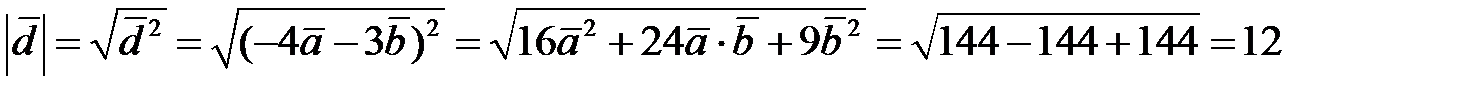 .
.
Косинус угла между векторами  и
и  равен
равен


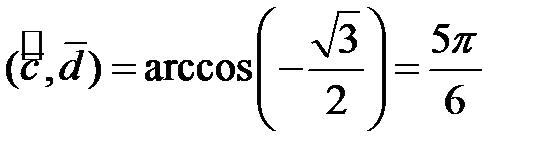 .
.
Ответ:  .
.
Пример решения задания №5. Даны координаты вершин пирамиды  . Найти:
. Найти:
1. длину ребра  ;
;
2. угол между ребрами  и
и  ;
;
3. угол между ребром  и гранью
и гранью  ;
;
4. площадь грани  ;
;
5. объем пирамиды;
6. уравнение ребра  ;
;
7. уравнение грани  .
.
 ,
,  ,
,  ,
,  .
.
| A0 |
| A3 |
| A2 |
| A1 |
Для решения задачи введем векторы:
 ,
,  ,
, 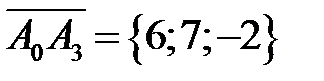 .
.
1) Длина ребра 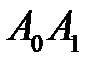 равна длине вектора
равна длине вектора 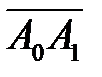 , т.е.
, т.е.  .
.
2) Найдем косинус угла  между ребрами
между ребрами  и
и  как косинус угла между векторами
как косинус угла между векторами 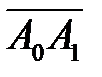 и
и  , используя определение скалярного произведения
, используя определение скалярного произведения
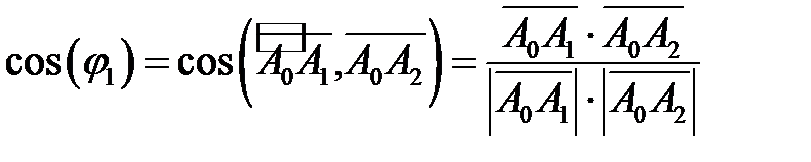 .
.
Так как
 ;
; 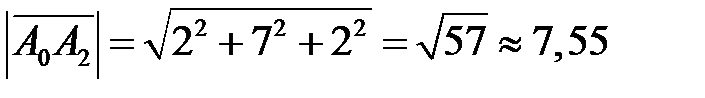 ;
;


 .
.
3) Синус угла  между ребром
между ребром 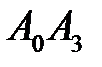 и гранью
и гранью  равен модулю косинуса угла между
равен модулю косинуса угла между  и нормальным вектором плоскости
и нормальным вектором плоскости  , который находится с помощью векторного произведения векторов
, который находится с помощью векторного произведения векторов
 ,
,
 .
.
Так как
 ;
;
 ;
; 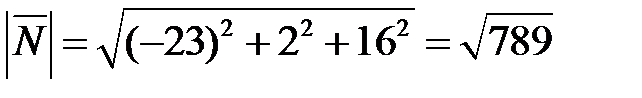 ;
;


 .
.
4) Площадь грани  находится по формуле
находится по формуле
 .
.
5) Объем V пирамиды  находится через абсолютную величину смешанного произведения векторов
находится через абсолютную величину смешанного произведения векторов 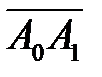 ,
,  ,
,  .
.
 .
.
6) Канонические уравнения прямой  записываются в виде
записываются в виде
 ,
,
где  координаты точки
координаты точки  , а
, а  - координаты точки
- координаты точки  .
.
Таким образом,
 .
.
7) Уравнение плоскости  имеет вид
имеет вид
 ,
,
где 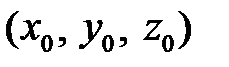 - координаты точки
- координаты точки  ;
;
 – координаты точки
– координаты точки  ;
;
 – координаты точки
– координаты точки  .
.
Таким образом,




 или
или
 .
.
Сделаем проверку полученного уравнения, подставив координаты точек  ,
,  ,
,  в это уравнение.
в это уравнение.

Получены верные равенства, значит уравнение плоскости составлено верно.
Ответ: 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  ; 7)
; 7)  .
.
Пример решения задания № 6. Найти уравнение геометрического места точек, для каждой из которых отношение расстояния до точки  к расстоянию до прямой
к расстоянию до прямой  постоянно и равно
постоянно и равно  . Сделать чертеж полученной линии.
. Сделать чертеж полученной линии.
Решение
Для наглядности отметим на координатной плоскости точку  и заданную линию. Обозначим точку, лежащую на предполагаемой линии,
и заданную линию. Обозначим точку, лежащую на предполагаемой линии,  ; расстояние от
; расстояние от 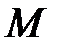 до прямой обозначим
до прямой обозначим  , от
, от 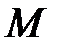 до
до  обозначим
обозначим 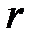 .
.
 .
.
 .
.
По условию задачи
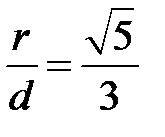 или
или  .
.
Возведем в квадрат обе части уравнения.




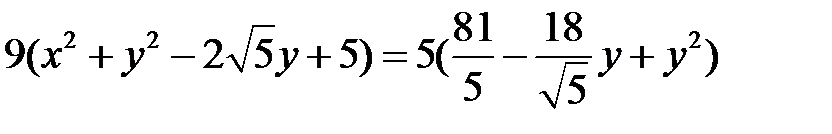






|


 .
.
Получили каноническое уравнение эллипса.
Вершины эллипса:  ,
,  ,
,  ,
,  . Чтобы изобразить эллипс, отметим его вершины на координатной плоскости и соединим их плавной линией.
. Чтобы изобразить эллипс, отметим его вершины на координатной плоскости и соединим их плавной линией.
Справочный материал для выполнения задания 6.
Эллипс
Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная, равная  . Расстояние между фокусами равно
. Расстояние между фокусами равно 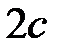 . Каноническое уравнение эллипса
. Каноническое уравнение эллипса
 , где
, где 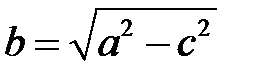 .
.
Если фокусы эллипса расположены на  , то
, то  ; если фокусы расположены на
; если фокусы расположены на 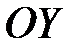 , то
, то  .
.
|
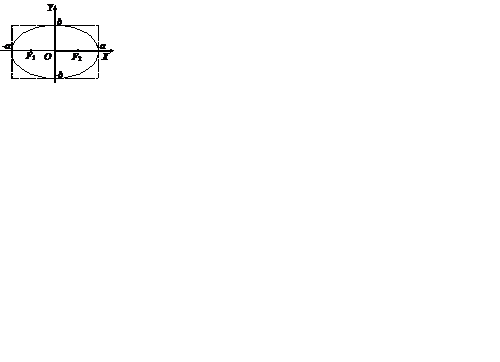
Для изображения эллипса построим прямоугольник со сторонами  (по оси
(по оси  ) и
) и  (по оси
(по оси 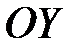 ) и с центром в начале координат. В полученный прямоугольник впишем эллипс.
) и с центром в начале координат. В полученный прямоугольник впишем эллипс.
Если уравнение эллипса имеет вид;
 ,
,
то его центр находится в точке  .
.
Гипербола
Гиперболой называется геометрическое место точек, для которых разность расстояний до двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная, равная  . Расстояние между фокусами
. Расстояние между фокусами  (
( ).
).
Каноническое уравнение гиперболы
 , где
, где 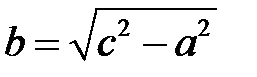 .
.
Если фокусы гиперболы расположены на 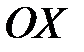 , то
, то  , если фокусы расположены на
, если фокусы расположены на  , то
, то  . Гипербола с уравнением
. Гипербола с уравнением 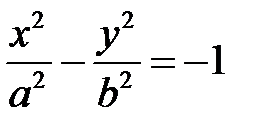 называется сопряженной к гиперболе с уравнением
называется сопряженной к гиперболе с уравнением  .
.

|
Для изображения гиперболы построим прямоугольник со сторонами  (по оси
(по оси  ) и
) и  (по оси
(по оси 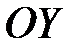 ) и с центром в начале координат. В прямоугольнике проводим диагонали (с продолжением), которые являются асимптотами гиперболы, вершины которой находятся в точках
) и с центром в начале координат. В прямоугольнике проводим диагонали (с продолжением), которые являются асимптотами гиперболы, вершины которой находятся в точках  и
и  . Ветви гиперболы с уравнением
. Ветви гиперболы с уравнением  проходят через точки
проходят через точки  и
и  . Ветви сопряженной гиперболы проходят через точки
. Ветви сопряженной гиперболы проходят через точки  и
и  .
.
Если уравнение имеет вид
 ,
,
то центр гиперболы находится в точке  .
.
Парабола
Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Если координаты фокуса  , уравнение директрисы
, уравнение директрисы  , то каноническое уравнение параболы
, то каноническое уравнение параболы  задает параболу с вершиной в начале координат, симметричную относительно оси
задает параболу с вершиной в начале координат, симметричную относительно оси  . При
. При  ветви параболы направлены в положительном направлении оси
ветви параболы направлены в положительном направлении оси  , при
, при 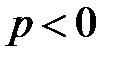 – в противоположную сторону.
– в противоположную сторону.
Если координаты фокуса 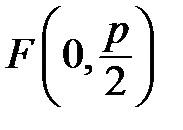 , уравнение директрисы
, уравнение директрисы  , то каноническое уравнение параболы
, то каноническое уравнение параболы  задает параболу с вершиной в начале координат симметричную относительно оси
задает параболу с вершиной в начале координат симметричную относительно оси 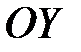 . При
. При  ветви параболы направлены вверх, при
ветви параболы направлены вверх, при 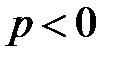 – вниз.
– вниз.