ХАРАКТЕРИСТИКИ ВАРИАЦИОННОГО РЯДА. СТРУКТУРНЫЕ СРЕДНИЕ
Мода – значение признака, наиболее часто встречающегося в исследуемой совокупности.
Медиана – значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.
Для дискретных вариационных рядов модой будет значение варианта с наибольшей частотой. Вычисление медианы в дискретных рядах распределения имеет специфику. Если такой ряд распределения имеет нечётное число членов, то медианой будет вариант, находящийся в середине ранжированного ряда. Если ранжированный ряд распределения состоит из чётного числа членов, то медианой будет средняя арифметическая из двух значений признака, расположенных в середине ряда.
Пример. Рассчитаем моду и медиану по данным табл. 7.10.
Т а б л и ц а 7.10.
Распределение обуви, проданной коммерческой фирмой в январе 2008г.
| Размер | Me | 42 Mo | 44 и более | Итого | ||||||||
| Количество проданных пар, % к итогу | ||||||||||||
| Накопленные частоты | - |
В этом ряду распределения мода равна 42. Именно этот размер обуви в январе 2008 г. пользовался наибольшим спросом.
Для определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание продолжается до получения накопленной суммы частот, впервые превышающей половину. В нашем примере сумма частот составила 100, её половина – 50. Накопленная сумма частот ряда равна 62. Ей соответствует значение признака равное 40. Таким образом, 40-й размер обуви является медианным.
Для интервальных вариационных рядов мода определяется по формуле:

где xMo – нижняя граница значения интервала, содержащего моду;
iMo – величина модального интервала;
fMo – частота модального интервала;
fMo–1 – частота интервала, предшествующего модальному;
fMo+1 – частота интервала, следующего за модальным.
Медиана интервального ряда распределения определяется по формуле:
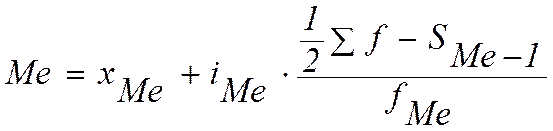 ,
,
где xMe – нижняя граница значения интервала, содержащего медиану;
iMe – величина медианного интервала;
∑f – сумма частот;
SMe-1 – сумма накопленных частот, предшествующих медианному интервалу;
fMe – частота медианного интервала.
Пример. Рассчитаем моду и медиану по данным табл. 7.11.
 руб.
руб.
Следовательно, наибольшее число семей имеют среднедушевой доход 772 руб.
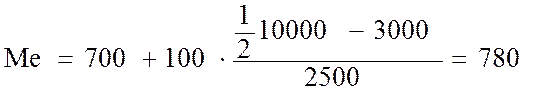 руб.
руб.
Таким образом, половина семей города имеет среднедушевой доход менее 780 руб., остальные семьи – более 780 руб.
Т а б л и ц а 7.11.
Распределение семей города по размеру среднедушевого дохода в январе 1998 г.
| Группы семей по размеру дохода, руб. | Число семей fi | Накопление частоты | Накопление частоты, % к итогу | ||||
До 500
500 – 600

800 – 900 900 – 1000 Свыше 1000 | |||||||
| Итого | ∑fi | - | - |
Аналогично с нахождением медианы в вариационных рядах можно отыскать значение признака у любой по порядку единицы ранжированного ряда. Например, можно найти значение признака у единиц, делящих ряд на четыре равных части, десять или сто частей. Эти величины называются «квартили», «децили» и «перцентили».
Квартили представляют собой значение признака, делящее ранжированную совокупность на четыре равновеликие части. Различают квартиль нижний (Q1), отделяющий ¼ часть совокупности с наименьшим значением признака, и квартиль верхний (Q3), отсекающий ¼ часть с наибольшими значениями признака. Это означает, что 25% единиц будут заключены меньше по величине Q1; 25% единиц будут заключены между Q1 и Q2; 25% - между Q2 и Q3 и остальные 25% превосходят Q3. Средним квартилем Q2 является медиана.
Для расчёта квартилей по интервальному вариационному ряду используют формулы:
 ;
;
 ,
,
где xQ1 – нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%);
xQ3 – нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%);
SQ1-1 – накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;
SQ3-1 – накопленная частота интервала, предшествующего интервалу, содержащему верхний квартиль;
fQ1 – частота интервала, содержащего нижний квартиль;
fQ3 – то же для верхнего квартиля.
Рассмотрим расчёт нижнего и верхнего квартилей по данным табл. 7.11. Нижний квартиль находится в интервале 600-700, накопленная частота которого равна 30%. Верхний квартиль лежит в интервале 800-900 с накопленной частотой 77%. Поэтому получим:
 руб.
руб.
 руб.
руб.
Вывод: 25% семей имеют среднедушевой доход менее 671 руб., 25% семей – свыше 891 руб., а остальные имеют доход в пределах 671 – 891 руб.
Децили – вариации, делящие ранжированный ряд на десять равных частей. Первый дециль d1 делит совокупность в соотношении 1/10 к 9/10; второй дециль d2 – в соотношении 2/10 к 8/10 и т. д.
Вычисляются они по той же схеме, что медиана и квартили:



 700 – 800
700 – 800