Кафедра энергии и окружающей среды
Э.М. Абадеев
Методические указания
к решению контрольных задач
по теоретической механике.
Учебно-методическое пособие
Дубна
2011г.
Контрольные работы по теоретической механике охватывают три основных раздела этой дисциплины – статику, кинематику и динамику. Каждая контрольная работа выполняется и сдается на проверку отдельно в сроки, предусмотренные учебным графиком, в соответствии с индивидуальным номером варианта, заданного студенту. Задачи контрольных работ приведены в методическом сборнике, имеющемся на кафедре в печатном и электронном видах. Выполнение работ с использованием компьютерных технологий приветствуется.
Раздел 1. Статика.
В разделе статики студентам предлагаются для решения три типовые задачи:
- задача С-1 - на разложение заданной силы по заданным направлениям на плоскости;
- задача С-2 – на определение реакций опор составной балки, нагруженной произвольной системой сил на плоскости;
- задача С-3 - на определение реакций опор твердого тела, нагруженного произвольной системой сил в пространстве.
Задача С-1.
К кронштейну с стержнями 1 и 2, веса которых не учитываются, приложена сила Р =15кН. Найти усилия в стержнях F 1 и F 2. Углы, обозначенные на схеме, имеют величины: a=24°, b=39°, g=23°.
Решение.
Задача может быть решена несколькими способами. Рассмотрим три из них.
1. Мысленно вырежем т. С и рассмотрим ее равновесие под действием заданной и искомых сил. Аналитические условия равновесия т. С под действием пучка сил (Р,F 1, F 2) в проекциях на оси х, у записываются:
ΣХ = 0; Pcos g -F 1 +F 2 cos φ = 0;
ΣY = 0; Psin g- F 2 sin φ = 0. (1)
Следует обратить внимание на выбор системы координатных осей х, у. На рис.1 они выбраны таким образом, чтобы одна из осей прошла бы вдоль одного из стержней. В таком случае в системе (1) одно из уравнений непосредственно дает величину одной из двух неизвестных, после чего из второго уравнения находится вторая искомая величина.
Очевидно, φ = 180° - (a+ b) = 119°. Подстановка всех данных в систему (1) дает:
15co s 23° -F 1 +F 2 cos 119° = 0,
15 sin 23°- F 2 sin 119° = 0,
откуда F 2 = 
[кН];
F 1= 15*0,9205 – 6,70*0,4848=10,56 [кН].
2. Для следующих двух способов решения задачи, связанных с геометрическими построениями, необходимо схему кронштейна представлять не произвольно, как на рис. 1, а изображать в соответствии с заданными величинами углов a, b, g (Рис. 2).
Геометрическое условие равновесия т. С под действием пучка сил (Р,F 1, F 2) состоит в требовании замкнутости силового треугольника, построенного на векторах этих сил.
Поэтому второй способ решения задачи может состоять, например, в применении теоремы синусов к треугольнику АВС. Предварительно определим угол δ = 180° - φ – γ =180° – 119° – 23° = 38°. Далее запишем соотношения теоремы синусов:
;
.
Третий способ состоит в том, чтобы на рис. 2 определить масштаб сил по известной величине Р и определить искомые силы по замерам с рис. 2 и вычисленному масштабу. По рис. 2 масштаб определяется:
В таком случае
Полученные этим способом результаты могут считаться достаточно точными для графо-аналитического метода.
Задача С-2.
Найти реакции в опорах А, В, С и шарнире D сочлененной балки (рис. 1). Заданные величины: Р1 = 3кН, Р2 = 5кН, q = 9кН/м, m = 0,5кНм, a = 60°, a = 0,4м, b = 0,5м, c = 0,3м, d = 0,2м, e = 0,3м, l = 1,2м.
Решение.
 |
Прежде всего, доопределим недостающий размер f = l - c - d - e = 0,4м.
Далее, в соответствии с условными обозначениями опор, изобразим искомые реакции опор А, В, С и шарнира D. При этом разделим сочлененную балку по шарниру D на левую АD и правую DА части (рис. 2). Выберем оси координат (ху), в которой будем составлять системы уравнений статического равновесия.
Изображенные на рис. 2 реакции шарнира D для левой и правой частей балки, в соответствии с аксиомой статики о силах взаимодействия двух тел, попарно равны по величине и противоположны по направлению: RDx = -R´Dx, RDy = - R´Dy.
С учетом сказанного в задаче всего 6 неизвестных: RА, RВx, RВу, RС, RDx, RDу. Таким образом, задача имеет единственное решение, т.к. для двух твердых тел на плоскости можно составить именно 6 уравнений равновесия:
Для левой балки –
ΣFix = 0; P1cosα + RDx = 0;
ΣFiу = 0; RА - P1sinα –q(b-a) + RDy = 0;
ΣMD = 0; -RАb + P1sinα(b-a) + q(b-a)2/2 = 0.
Для правой балки –
ΣFix = 0; - RDx + RBx = 0;
ΣFiy = 0; - RDy – qc + RBy + P2 + RC = 0;
ΣMB = 0; RDy(c+f) + qc(c/2+f) – m – P2d + RC(d+e) = 0.
При составлении уравнения моментов за точку приведения следует выбирать точку одной из опор, реакция которой неизвестна (для левой балки это т.А или т.D, для правой балки т.В или т.С; реакция RDy будет вычислена ранее).
Таким образом, получаем систему уравнений, разрешаемую в следующем порядке.
- P1cosα + RDx = 0; RDx = - P1cosα; RDx = -3cos60° = -1,5кН.
- -RDx + RBx = 0; RBx = RDx; RBx = -1,5кН.
3. -RАb + P1sinα(b-a) + q(b-a)2/2 = 0; RА = [P1sinα(b-a) + q(b-a)2/2]/b;
RА = [3sin60°(0,5-0,4) + 9(0,1)2/2]/0,5; RА = 0,6096кН.
4. RА - P1sinα –q(b-a) + RDy = 0; RDy = P1sinα + q(b-a) - RА = 3sin60° + 9(0,5-0,4)
– 0,6096; RDy = 2,888кН.
5. RDy(c+f) + qc(c/2+f) – m – P2d + RC(d+e) = 0; RC = [ - RDy(c+f) - qc(c/2+f) + m
+ P2d]/(d+e) = [-2,888(0,3 + 0,4) - 9×0,3(0,15+0,4) + 0,5 + 5×0,2]/(0,2 + 0,3);
RC = - 4,013кН.
6. - RDy – qc + RBy - P2 + RC = 0; RBy = RDy + qc + P2 - RC = 2,888+ 9×0,3 + 5 + 4,013;
RBy = 14,60кН.
Проверка правильности вычислений для каждой балки возможна путем составления уравнения моментов для другой точки приведения.
Для левой балки
ΣMА = 0; - P1sinα×a - q(b-a)(a + (b - a)/2) + RDyb = 0;
- 3sin60°×0,4 – 9(0,5 – 0,4)(0,4 + 0,1/2) + 2,888×0,5 = 0; 1,444 – 1,444 = 0.
Для правой балки
ΣMС = 0; P2×e - RBy(d + e) – m + qc(l – c/2) + RDy l = 0;
5×0,3 – 14,60(0,2 + 0,3) -0,5 + 9×0,3(1,2 – 0,3/2) + 2,888×1,2 = 0; 7,8 –7,8 = 0.
Задача С-3.
Однородная плита длиной а = 0,4м и шириной b = 0,3м имеет вес Р =1,5кН. Плита, закрепленная с помощью сферического шарнира В, цилиндрической петли А и стержня СЕ, наклоненного к плоскости плиты под углом a = 60°, нагружена силой
F = 3кН, равномерно распределенной нагрузкой q = 6кН/м и парой сил с моментом
m = 0,2кНм (рис.1). Определить реакции шарнира, петли и наклонного стержня.
Решение.
Изобразим искомые реакции опор А, В, С в соответствии с условными обозначениями опор. Цилиндрический шарнир (петля) А имеет две составляющие пространственной реакции, сферический шарнир В – три составляющие, а реакция стержня СЕ в точке С может направлена только вдоль оси стержня (рис.1).
Таким образом, в задаче 6 неизвестных: RАx, RАz, RВx, RВу, RBz, RС; задача имеет единственное решение, т.к. для твердого тела в трехмерном пространстве можно составить именно 6 уравнений равновесия:
1. ΣFix = 0; RАx + RВx - RСcosα = 0;
2. ΣFiу = 0; RВу = 0;
3. ΣFiz = 0; RАz + RBz - RСsinα – P – F - qa = 0.
4. ΣMx = 0; (RBz – RCsinα)a –Pa/2 – qa2/2 = 0;
5. ΣMy = 0; (RCsinα + F)b + Pb/2 + qab = 0;
6. ΣMz = 0; - RВxa + m + RC cosα a = 0.
Система решается в следующем порядке.
1. RВу = 0.
2. Из пятого уравнения находим RС = -(F + P/2 + qa)/ sinα; RС = - (3 + 1,5 + 6×0,4)/sin60°. RС = - 7,967кН. Знак – означает, что на самом деле реакция в стержне СЕ направлена в противоположную сторону.
3. Из шестого уравнения определяем RВx = (m/a + RC cosα); RВx = (0,2/0,4 - 7,967 cos60°). RBx = - 7,37335кН. Эта реакция также направлена в сторону, противоположную изображенной на рис 1.
4. Из первого уравнения находим RАx = RСcosα - RВx; RАx = -7,967 cos60° + 7,37335. RАx = 3,38985кН.
5. Из четвертого уравнения определяем RВz = RCsinα + P/2 + qa/2; RВz = - 7,967 sin60° + 1,5/2 + 6×0,4/2; RBz = - 4,950кН. Реакция также направлена в противоположную сторону по отношению к изображенной на рис 1.
6. Из третьего уравнения находим RАz = - RBz + RСsinα + P + F + qa; RАz = 4,950 + 7,967 sin60° +1,5 + 3 + 6×0,4. RАz = 18,75кН.
Окончательно величины реакций в опорах А и В находятся:
 |
RА = √(RАx2 + RАz2); RА = 19,05кН. RB = √(RBx2 + RBz2); RB = 8,881кН.
Раздел 2. Кинематика.
В разделе кинематики предлагаются для решения три типовые задачи:
- задача К-1 - на определение траектории и кинематических параметров криволинейного движения точки на плоскости;
- задача К-2 – на определение параметров движения точек и звеньев плоского рычажно – ползункового механизма с одной степенью свободы;
- задача К-3 - на определение параметров движения точки, совершающей сложное движение в пространстве.
Задача К-1.
Точка А движется в плоскости ху. Закон движения точки задан параметрическими уравнениями x = 3 t -8, y = 8 – 3 t 2, где x и y выражены в сантиметрах, t – в секундах..
Найти уравнение траектории и изобразить ее действительный вид. Нанести положение точки в заданный момент времени t 1 = 1,8с. Для этого момента определить скорость и полное ускорение точки, а также касательную и нормальную составляющие ускорения и радиус кривизны в соответствующей точке траектории.
Решение.
|
|
|
Видим, что траектория представляет собой квадратичную параболу с вершиной в т. х э = -8, y э = 24; ось параболы параллельна оси y; ветви параболы направлены вниз (рис.1). При t 1 = 1,8с точка имеет координаты x = -2,6; y = – 1,72 (показана на рис. 1 знаком ▫).
|
где 
. При t 1 = 1,8с 
, т.е. 
см/с.
3. Полное ускорение точки находится по формуле
и при 
имеем 
см/с2.
Касательное ускорение, по определению, представляет собой производную по времени от скорости точки, т.е.
,
и при t 1 = 1,8с получаем 
см/с2.
Нормальное ускорение точки определяется из соотношения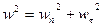 
, откуда получаем 
см/с2.
Радиус кривизны траектории в заданный момент времени находится по формуле
см.
Задача К-2.
Плоский механизм состоит из стержней 1, 2, 3 и ползунов В и D (рис. 1). Стержни соединены друг с другом, с ползунами и с опорой О шарнирами; точка С находится в середине стержня АВ. Длины стержней равны соответственно: l1 = 0,4м, l2 = 1,2м, l3 = 1,4м. Заданная угловая скоростьω1 = 4рад/с.
Требуется определить скорости всех точек механизма, угловую скорость и угловое ускорение звена АВ, а также ускорение точки В.
Решение.
1. Решение необходимо начинать с определения скорости т.А, принадлежащей ведущему звену ОА, угловая скорость которого ω1 = 4рад/с = const.
В этом случае VА = ω1 × l 1 = 1,6м/с. При этом известно также направление этого вектора (см. рис. 1).
Поскольку направление скорости т.В также известно (ползун В движется вдоль направляющей), можно найти мгновенный центр вращения звена АВ как точку М пересечения перпендикуляров к скоростям этих точек.
В треугольнике АВМ углы МВА и АМВ равны, поэтому АМ = АВ = 1,2м. Зная величину скорости т.А, находим угловую скорость вращения звена АВ:
ωАВ = VА/ АВ = 1,6/1,2 = 1,333 рад/с.
Направление этой угловой скорости соответствует направлению вектора скорости 
.
Из треугольника АВМ с учетом его равнобедренности и величины угла при вершине по теореме косинусов находим ВМ2 = 2АВ2 - 2АВ×АВ×cos120°;
ВМ = AB√3 = 2,08м.
Тогда скорость т.В определяется как VВ = ωАВ × ВМ = 2,74м/с.
Из треугольника АСМ, учитывая, что АС = СВ = 0,6м, по теореме косинусов находим СМ2 = АМ2 + АC2 - 2АM × АВC × cos120°;
CМ = 1,8м.
Величину угла АСМ определим из треугольника АСМ по теореме синусов:
Sin(
ACM)/AM = sin( MAC)/CM,
откуда sin( ACM) = sin120°× АМ/СМ = 0,866× 1,2/1,8 = 0,577; АСМ = 35,24°.
Скорость т.С определяется как VС = ωАВ × СМ = 2,4м/с. Вектор скорости т.С 
перпендикулярен СМ и направлен по направлению угловой скорости ωАВ. Поэтому угол φ между вектором и звеном СД определяется:
φ = 90° - АСМ - АСД = 90° - 35,24° - 30° = 24,76°.
Скорость т. D определяется по теореме о проекции скоростей двух точек звена, совершающего плоско-параллельное движение, на линию, их соединяющую:
Пр 
|СD = Пр 
|СD, 
или V Dcos60° = V C cos24,76°, откуда V D = 4,36м/с.
2. Ускорение т.А, принадлежащей ведущему звену ОА, угловая скорость которого ω1 = 4рад/с = const, определяется по формуле WA = 
= 6,4м/с2. При этом известно также направление этого вектора (см. рис. 1).
Ускорение т.В, принадлежащей звену АВ, определяется из векторного уравнения
Направления всех векторов этого уравнения известны, вектора показаны на рис. 1. Кроме того, величина ускорения 
также определяется:
м/с2.
Для определения оставшихся двух неизвестных (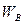
, 
) спроектируем векторное уравнение на оси х, у, показанные на рис.1.
На рис.1 оси х, у выбраны таким образом (вдоль звена АВ и перпендикулярно ему), что записанная выше система уравнений существенно упрощается. Действительно, запишем выражения для проекций, входящих в систему:
м/с2;
м/с2;
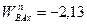м/с2;
Таким образом, система уравнений для определения двух неизвестных 
, принимает вид:
м/с2;
Из первого уравнения находится величина абсолютного ускорения
т.В 
=10,66м/с2, из второго уравнения – величина тангенциальной составляющей ускорения т.В в относительном (вращательном) движении
т.В относительно т.А = 14,77м/с2.
Последняя искомая величина – угловое ускорение звена АВ - находится из формулы
1/с2.
Задача К-3.
Круглая пластина (рис. 1) радиуса r = 80см вращается вокруг оси ОО1 по закону j = 5t - 4t2 (t – сек, j - рад).
По пластине по дуге AD окружности движется точка М; закон ее относительного движения s(t) = AM = pr(t3 – 2t2)/3 где s – в сантиметрах, t – в секундах. На рисунке точка М показана в положении, при котором s>0 (при s<0 точка М находится по другую сторону от точки А).
Требуется найти абсолютную скорость и абсолютное ускорение точки М в момент времени t1 = 4с.
Решение.
Прежде всего, изобразим т.М в её положении в момент времени t1 = 4с.
s(t=4c) = pr(43 – 2×42)/3 = 
pr,
т.е. точка М в относительном движении по окружности радиуса r совершит 5 полных оборотов и еще переместится на120° относительно т.А. Истинное положение т.М в заданный момент времени показано на рис. 1.
1. Определим параметры относи-тельного движения.
Относительная скорость направлена по касательной к окружности диска, проведенной в т.М и определяется по формуле
При R = 80см, t1 = 4с получаем
см/с=26,81м/с.
Тангенциальное ускорение в относительном движении также направлено по касательной к окружности диска и определяется по формуле 
; при t1 = 4с получаем 
см/с2=16,75м/с2.
Нормальное ускорение в относительном движении направлено по радиусу диска к его центру и определяется по формуле 
; при t1 = 4с получаем 
м/с2.
2. Определим параметры переносного движения.
Переносная скорость направлена перпендикулярно к плоскости рис.1 в направлении вращения диска – вдоль оси z абсолютной системы координат xyz, изображенной на рис. 1. Величина переносной скорости определяется из соотношения
где R – расстояние от т.М до оси вращения диска; при t1 = 4с получаем 
см = 1,467м. Величина переносной скорости:
см/с = -39,61м/с.
Знак «–» означает, что вектор переносной скорости направлен вдоль отрицательного направления оси z.
Тангенциальное ускорение в переносном движении направлено также вдоль оси z и определяется по формуле 
(не зависит от времени); 
см/с2 = -11,74м/с2. Эта составляющая ускорения направлена также вдоль отрицательного направления оси z.
Нормальное ускорение в переносном движении направлено по нормали к оси диска, проведенной из т.М и определяется по формуле 
; при
t1 = 4с получаем 
м/с2.
Поскольку переносное движение – вращательное, возникает еще и кориолисова составляющая абсолютного ускорения. Эта составляющая определяется из векторного соотношения
.
Угловая скорость переносного движения 
1/с, т.е. направлена по часовой стрелке, глядя из т.О1. Поэтому вектор 
направлен от т.О1 к т.О. В этом случае кратчайший поворот вектора до совпадения с вектором 
производится против часовой стрелки, т.е.вектор 
направлен вдоль оси z в положительном её направлении.
Величина кориолисового ускорения определяется формулой 
м/с2.
3. Определим параметры абсолютного движения т.М.
Величина абсолютной скорости т.М определяется непосредственно через величины относительной и переносной скоростей, т.к. эти составляющие взаимно перпендикулярны.
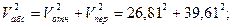
м/с.
Для определения величины абсолютного ускорения необходимо спроектировать все его составляющие на оси выбранной ортогональной системы координат xyz. Поскольку 
, получим:
= 1532м/с2.
м/с2.
м/с2.
Таким образом, величина абсолютного ускорения определяется:
м/с2.
Раздел 3. Динамика.
В разделе динамики предлагаются для решения три типовые задачи:
- задача Д-1 - на определение закона движения точки, совершающей вынужденные колебания при наличии сопротивления;
- задача Д-2 – на определение скорости движения тел с использованием теоремы об изменении кинетической энергии системы;
- задача Д-3 - на определение ускорения движения тел с использованием общего уравнения динамики или уравнения Лагранжа второго рода.
Задача Д-1.
Груз 1 массой m = 0,8 кг укреплён на пружинной подвеске в лифте 2 (жесткости пружин С1 = 80 Н/м, С2 = 120 Н/м, С3 = 160 Н/м). Лифт движется вертикально по закону
z = 
a1t2 + a2sinwt, (1)
гдеz направлена по вертикали вверх; величина zвыражена в метрах, t – в секундах;
а1 = 9,81 м/с2, а2 = 0,2 м, w = 10 1/с.
На груз действует сила сопротивления среды R = mv, где v – скорость груза по отношению к лифту, коэффициент сопротивления среды m = 8Нс/м. Вначале грузу сообщается скорость v0 = 2м/с при нулевом начальном отклонении от положения статического равновесия груза.
Вес соединительной планки между пружинами и пружин не учитывается.
Найти закон движения груза по отношению к лифту.
Решение.
Предложенная задача относится к задачам на составление и решение уравнения движения исследуемого тела. При этом по условию задачи требуется найти решения этого уравнения в движущейся системе координат, связанной с лифтом; закон движения лифта относительно неподвижной системы координат известен.
1. Решение задачи должно начинаться с замены заданной системы пружин одной эквивалентной пружиной.
Вначале заменим пружины 1 и 2 одной эквивалентной пружиной Э1. Если вес груза, подвешенного к двум последовательно соединенным пружинам, равен mg, то под действием этой силы, одинаково действующей на обе пружины, пружины растянутся на длину
, 
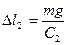, (2)
т.е. суммарное удлинение составит 
(3)
Эквивалентной пружиной Э1, очевидно, считается такая, удлинение которой равно удлинению заменяемой системы при той же нагрузке. Таким образом,
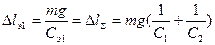, откуда 
, т.е.
. (4)
Заменяя теперь эквивалентной пружиной Э пружины Э1 и 3, заметим, что удлинение пружины Э1, очевидно, по величине равно укорочению пружины 3 и равно удлинению эквивалентной пружины Э, т.е.
,
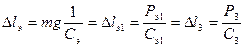причем, очевидно, 
, или 
, т.е.
,
и окончательно
. (5)
В данной задаче 
Н/м.
Отметим, что здесь рассмотрены два варианта комбинаций двух пружин – последовательное и встречное соединение. Для третьей возможной комбинации – параллельного соединения пружин С1 и С2 по аналогии легко получить формулу 
.
2. Получив новую схему задачи, изобразим ее на рис. 2. Выберем следующие оси координат Ось неподвижную z, которая входит в закон движения лифта (1), направим вертикально вверх. Закон движения груза ищется по отношению к лифту. Поэтому выберем связанную с лифтом ось х таким образом, чтобы ее начало находилось в положении статического равновесия груза, а направление совпадало бы с направлением действия силы веса этого груза.
Выбор направления осей и начала отсчета на осях может быть произвольным, но предложенные здесь оси позволяют несколько упростить запись уравнений движения, что будет видно из хода решения задачи.
Изобразим на рис. 2 также действующие на груз силы.
Величина силы упругости пружины Fпр = Сэ|∆l|. Направлена эта сила в сторону, противоположную отклонению ∆ l. В данном случае ∆ l = λСТ + х, причем, очевидно, Сэ ∆lСТ = mg.
Таким образом, проекция упругой силы на ось х равна
Fпрх = - Сэ (λСТ + х)= - (mg +Cэ х). (6)
Величина силы сопротивления движению груза по условиям задачи определяется соотношением R = mv,
где v – скорость движения груза в данный момент времени, т.е. производная по времени от перемещения; 
. Направление силы сопротивления противоположно направлению скорости груза. Полагая в произвольный момент времени скорость, как и перемещение положительными, получаем, что проекция этой силы на ось х равна
(7)
Поскольку ищется уравнение относительного движения, в правую часть к действующим силам mg, Fпр , R необходимо добавить силу инерции переносного движения Fин, полученную согласно закона движения лифта (1):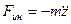 
и, следовательно, 
. С учетом противоположного направления оси х по отношению к оси z, получаем нужную нам проекцию:
. (8)
Уравнение движения груза в проекции на ось х записывается, с учетом (6)…(8):
(9)
при начальных условиях х (0)=0, 
3. Для решения уравнения (9) представим его в канонической форме:
(10)
где 
. В данной задаче 2n = 8/0,8 = 10 1/c; k 2 = 208/0,8 = 260 1/с2.
Решение неоднородного дифференциального уравнения (10) ищем в виде
,
где хобщ – общее решение однородного уравнения, соответствующего уравнению (10).
Решение однородного уравнения ищем способом подстановки Эйлера:
, т.е. 
, 
После сокращения на 
получаем характеристическое уравнение
.
В нашем случае корнями уравнения 
являются комплексные числа 
. Таким образом, общее решение однородного уравнения может быть представлено в виде
, (11)
где произвольные константы 
будут найдены в конце решения задачи из заданных начальных условий.
4. Частное решение уравнения (10) представляется в виде суммы двух решений: решения уравнения
(12)
и решения уравнения
. (13)
Для уравнения (12) решение очевидно:
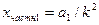, т.е. 
м. (14)
Решение уравнения (13) ищем в виде, соответствующем виду правой части:
(15)
Из (15) получаем:
(16)
Подставляя (15) и (16) в (13), получим, после раскрытия скобок в (14) и приведения подобных:
(17)
Для тождественного выполнения равенства (17) в любой момент времени необходимо и достаточно, чтобы множители при 
в левой и правой частях (17) были бы равны между собой, и также были бы равны между собой множители при 
в левой и правой частях. Таким образом получается система алгебраических уравнений для определения величин Р и βв выражении (15):
(18)
Система (18) легко решается:
; 
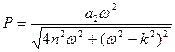. (19)
Подставляя в (19) числовые данные задачи, получим Р = -0,106м,
β = -0,559рад = -32°, т.е.
(20)
Окончательно решение уравнения (11) принимает вид
(21)
5. Для определения 
воспользуемся начальными условиями х (0) = 0, 
Из (21) получаем
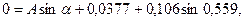т.е. 
(22)
Дифференцируя (21) по времени и подставляя t = 0, получаем
или, с учетом (22), А cosα = 0,1623. (23)
Из (22), (23) находим А = 0,1877, α = - 0,524рад = -30°.
Таким образом, искомое уравнение движения груза относительно лифта имеет вид:
. (24)
График x(t) представлен на рис. 3.
Задача Д- 2.
Механическая система (рис.1) состоит из сплошных однородных катков 1 (m 1=7кг) и 2 (m 2=4кг), ступенчатого шкива 3 (m 3=6кг) с радиусами ступеней R 3 = 0,3м, r 3 = 0,1м и радиусом инерции r 3 = 0,2м, блока 4 с массой m 4=5кг, равномерно распределённой по ободу, и грузов 5 (m 5=3кг) и 6 (m 6=8кг).
Коэффициент трения грузов о плоскости f тр = 0,1. Тела соединены нитями, перекинутыми через блоки и намотанными на шкив 3; участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жёсткости с= 80Н/м.
Система приходит в движение из состояния покоя под действием силы
F = 120(1+4 s), [ s ]=м, [ F ]=Н, зависящей от перемещения точки её приложения; s0 = 0, в момент начала движения деформация пружины равна нулю. При движении на шкив 3 действует постоянный момент сил сопротивления М =1,2Нм.
Определить значение V c2 в тот момент времени, когда перемещение s станет равным s 1 = 0,2м.
Решение.
Прежде всего, изобразим все действующие в системе внешние силы и моменты, предполагая, что перемещение системы происходит в направлении действия силы F.
1. Рассчитаем перемещения всех тел системы, когда груз 6 переместится на ∆s6.
Очевидно, перемещение блока 1 также будет равно этой величине (нити нерастяжимы), т.е.
δs 1 = δs 6, (1)
а угол его поворота определяется соотношением
. (2)
Угол поворота блока 4 вычисляется:
, (3)
а угол поворота блока 3 аналогично определяется как
. (4)
Угол поворота катка 2 (как подвижного блока) равен
(5)
а перемещение центра катка 2, равное перемещению груза 5 и деформации пружины,
(6)
2. Для решения задачи воспользуемся теоремой об изменении кинетической энергии системы материальных тел:
, (7)
причем, поскольку по условиям задачи движение системы начинается из со