Курсовая работа
По дисциплине«Информатика»
Разработка и анализ методов приближённых вычислений
определённого интеграла
средствами MS Excel
Выполнил: Смирнов А.В.
студент группы ЭТК 114-12 з Проверил: Кирсанова Н.В.
ст. преподаватель
г. Тверь, 2015
Приближенное вычисление определенного интеграла
I. Постановка задачи
В данной курсовой работе рассматривается задача нахождения численного значения определенного интеграла и методы, которые позволяют приближенно вычислить интеграл при помощи конечного числа значений интегрируемой функции. Эти методы могут применяться там, где другие подходы к вычислению интегралов оказываются бессильными. Кроме того, применение этих методов во многих случаях требует меньших затрат вычислительного труда, сравнительно с другими методами.
Цель данной работы – изучение простейших численных методов интегрирования и сравнение их точности.
Её содержанием является выполнение индивидуального задания по одному из предложенных вариантов двумя различными методами и сравнение их точности с использованием правила Рунге. Приводится описание теоретических вопросов, ответы на которые следует дать при защите работы.
Курсовая работа выполнена средствами MSExcel.
II. Анализ методов вычисления определенного интеграла
Пусть требуется вычислить определенный интеграл от непрерывной функции ƒ(х)
Если можно найти первообразнуюF(x) функции ƒ(х), то интеграл вычисляется по формуле Ньютона-Лейбница:
Но отыскание первообразной функции иногда весьма сложно; кроме того, как известно, не для всякой непрерывной функции ее первообразная выражается через элементарные функции. В этих и других случаях (например, функция
у = ƒ(х) задана графически или табличнo) прибегают к приближенным формулам, с помощью которых определенный интеграл находится с любой степенью точности.
Рассмотрим три наиболее употребительные формулы приближенного вычисления определенного интеграла — формулу прямоугольников, формулу трапеций, формулу парабол (Симпсона), основанные на геометрическом смысле определенного интеграла.
Формула центральных прямоугольников
Пусть на отрезке [а; b], а < b, задана непрерывная функция ƒ(х). Требуется вычислить интеграл 
численно равный площади соответствующей криволинейнойтрапеции (рис.1).
Рис.1. Метод центральных прямоугольников.
Разобьем основание этой трапеции, т. е. отрезок [а; b], на n равных частей
(отрезков) длины (шаг разбиения) с помощью точек х0= а, x1, х2,..., хn = b. Можно записать, что хi= х0+h• i, где i = 1,2,..., n (см. рис.1).
В середине 
каждого такого отрезка построим ординату ŷi =ƒ(сi) графика функции у = ƒ(х). Приняв эту ординату за высоту, построим прямоугольник с площадью h • ŷi.
Тогда сумма площадей всех n прямо угольников дает площадь ступенчатой фигуры, представляющую собой приближенное значение искомого определенного интеграла
|
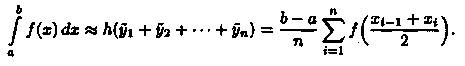
Формула (1) называется формулой центральных (средних) прямоугольников.
Абсолютная погрешность приближенного равенства (1) оценивается с помощью формулы:
где М2 — наибольшее значение |ƒ"(х)| на отрезке [а; b],
Отметим, что для линейной функции (ƒ(х)=kх+b) формула (1) дает точный результат, поскольку в этом случае ƒ"(х)=0.
|
|
|
|
|
|
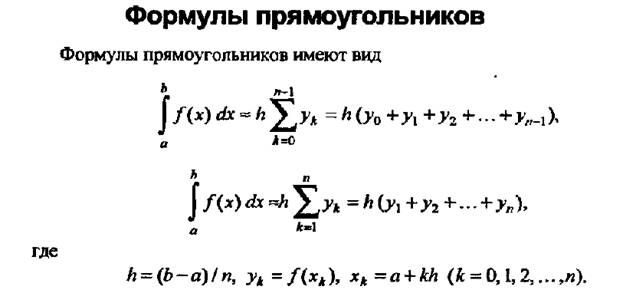
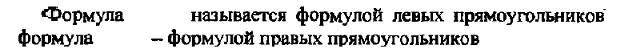
Рис.2 а. Метод левых Рис.2 б. Метод правых
прямоугольников.прямоугольников.
Формула трапеций
Формулу трапеций получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обычной трапецией.
Разобьем отрезок [а; b] на n равных частей длиныАбсциссы точек деления а = х0, x1,х2,...,b = хn (рис. 3). Пусть у0,у1,...,уn—соответствующие им ординаты графика функции.
Рис. 3. Метод трапеций
Расчетные формулы 
для этих значений имеют вид хi= a+h*i, уi=ƒ(xi), i= 0,1,2,..., n.
Заменим кривую у=ƒ(х) ломаной линией, звенья которой соединяют концы ординат yiи yi+1 (i = 0,1,2,...,n). Тогда площадь криволинейной трапеции приближенно равна сумме площадей обычных трапеций с основаниями уi, yi+1 и высотой 
или
|
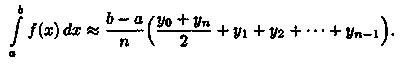
Формула (5) называется формулой трапеций.
Абсолютная погрешность Rn приближения, полученного по формуле трапеций, оценивается с помощью формулы 
• М2,
где 
Снова для линейной функции у=kх +b формула (5) — точная.