Классификация игр
Игры классифицируются по целому ряду признаков
1) По количеству игроков: парные игры (игры двух лиц) и игры n лиц (множественные игры) В парной игре число участников равно двум, в множественной - более двух.
2)По числу стратегий каждого игрока конечные (множество стратегий конечно) и бесконечные (множество стратегий каждого игрока бесконечно).
3) По характеру взаимоотношений: бескоалиционные, коалиционные, кооперативные игры. Бескоалиционными называются игры, в которых игроки не имеют право вступать в соглашения, образовывать коалиции, и целью каждого игрока является получение по возможности наибольшего индивидуального выигрыша. Игры, в которых действия игроков направлены на максимизацию выигрышей коллективов (коалиций) без последующего их разделения между игроками, называются коалиционными;
Исходом кооперативной игры является дележ выигрыша коалиции, который возникает не как следствие тех или иных действий игроков, а как результат их наперед определенных соглашений.
В соответствии с этим в кооперативных играх сравниваются по предпочтительности не ситуации, как это имеет место в бескоалиционных играх, а дележи; и сравнение это не ограничивается рассмотрением индивидуальных выигрышей, а носит более сложный характер;
4) По характеру выигрышей: игры с нулевой суммой (антагонистические) и игры с ненулевой суммой (неантагонистические). Очевидно, что парная игра с нулевой суммой является антагонистической, так как выигрыш одного игрока равен проигрышу второго, а следовательно цели этих игроков прямо противоположны.
5) По количеству ходов: одношаговые и многошаговые игры (позиционные, стохастические, дифференциальные) Позиционные игры задаются в виде дерева игры. Но любая позиционная игра может быть сведена к нормальной форме, в которой каждый из игроков делает только по одному независимому ходу. В позиционных играх ходы делаются в дискретные моменты времени. Существуют дифференциальные игры, в которых ходы делаются непрерывно. Эти игры изучают задачи преследования управляемого объекта другим управляемым объектом с учетом динамики их поведения, которая описывается дифференциальными уравнениями;
6) По количеству информации, имеющейся у игроков относительно прошлых ходов, игры подразделяются на игры:
с полной информацией (все стратегии игроков известны заранее; примеры: крестики-нолики, шашки, шахматы);
игры с неполной информацией (игра в карты (когда все карты розданы), домино);
7) По виду функций выигрыша: матричные, биматричные, непрерывные.
Конечная парная игра с нулевой суммой называется матричной игрой. Такая игра описывается платежной матрицей, в которой задаются выигрыши первого игрока. Номер строки матрицы соответствует номеру применяемой стратегии первого игрока, столбец - номеру применяемой стратегии второго игрока; на пересечении строки и столбца находится соответствующий выигрыш первого игрока (проигрыш второго игрока).
Конечная парная игра с ненулевой суммой называется биматричной игрой. Такая игра описывается двумя платежными матрицами, каждая для соответствующего игрока.
8) Повидам ходов игры подразделяются на стратегические и азартные. Азартные игры состоят только из случайных ходов - ими теория игр не занимается. Если наряду со случайными ходами есть личные ходы, или все ходы личные, то такие игры называются стратегическими.
В теории игр предполагается, что игра состоит из ходов, выполняемых игроками одновременно или последовательно. Ходы бывают личными и случайными. Ход называется личным, если игрок сознательно выбирает его из совокупности возможных вариантов действий и осуществляет его (например, любой ход в шахматной игре). Ход называется случайным, если его выбор производится не игроком, а каким-либо механизмом случайного выбора (например, по результатам бросания монеты).
Совокупность ходов, предпринятых игроками от начала до окончания игры, называется партией
Одним из основных понятий теории игр является понятие стратегии.
Стратегией игрока называется совокупность правил, определяющих выбор варианта действий при каждом личном ходе в зависимости от ситуации, сложившейся в процессе игры.
В простых (одноходовых) играх, когда в каждой партии игрок может сделать лишь по одному ходу, понятие стратегии и возможного варианта действий совпадают. В этом случае совокупность стратегий игрока охватывает все возможные его действия, а любое возможное для игрока I действие является его стратегией. В сложных (многоходовых) играх понятие «варианта возможных действий» и «стратегии» может отличаться друг от друга.
Стратегия игрока называется оптимальной, если она обеспечивает данному игроку при многократном повторении игры максимально возможный средний выигрыш или минимально возможный средний проигрыш, независимо от того, какие стратегии применяет противник. Могут быть использованы и другие критерии оптимальности.
Возможно, что стратегия, обеспечивающая максимальный выигрыш, не обладает другим важным представлением оптимальности, как устойчивостью (равновесностью) решения. Решение игры является устойчивым (равновесным), если соответствующие этому решению стратегии образуют ситуацию, которую ни один из игроков не заинтересован изменить.
1.3 Теоремы матричных игр
1. 3.1 Максиминная теорема
Если игрок А выбирает смешанную стратегию SA=||p1, p2,..., pm||, а игрок смешанную стратегию SB=||q1, q2,..., qn||, то средний выигрыш математическое ожидание выигрыша игрока А (проигрыша игрока В) определится суммой
 ,
,
которая может рассматриваться в качестве характеристики выбора SА и SB.
Формируя свою стратегию SА в антагонистической игре, игрок А в соответствии с принципом максимина должен выбрать такую стратегию, при которой минимально возможный выигрыш был бы максимален, т. е. такую стратегию, которая обеспечивает

Аналогичные рассуждения, связанные с поиском оптимальной смешанной стратегии игрока В, приводят к рекомендации выбрать такую стратегию SB, которая обеспечивает
 .
.
Весьма важным для теории и практики является вопрос о том, связаны ли между собой VА и VB. Ответ на него дает теорема о максимине.
В конечной игре двух игроков (коалиций) с нулевой суммой (матричной игре) при  имеет место равенство
имеет место равенство
 .
.
Теорема о максимине указывает на существование равновесия для случая VА=VB, при  и, следовательно, существования оптимальных смешанных стратегий
и, следовательно, существования оптимальных смешанных стратегий
Поэтому другая формулировка теоремы о максимине, называемая основной теоремой матричных игр определяется следующим образом.
1. 3.2 Основная теорема матричных игр.
Любая матричная игра имеет, по крайней мере, одно оптимальное решение, в общем случае, в смешанных стратегиях и соответствующую цену V.
Обе эти теоремы эквивалентны. Из этих теорем следует, что любая матричная игра имеет цену V. Цена игры V - средний выигрыш, приходящийся на одну партию, - всегда удовлетворяет условию
A£n£b,
т. е. лежит между нижней a и верхней b ценами игры.
Оптимальное решение игры в смешанных стратегиях, также как и решение в чистых стратегиях, обладает тем свойством, что каждый из игроков не заинтересован в отходе от своей оптимальной смешанной стратегии, если его противник применяет свою оптимальную смешанную стратегию, так как это ему невыгодно.
Важнейшим вопросом в теории игр (в том числе и матричных) является вопрос о выборе оптимальных стратегий для каждого из игроков.
Оптимальной стратегией игрока в матричной игре называется такая, которая обеспечивает ему максимальный выигрыш. Если игра повто- ряется неоднократно, то оптимальная стратегия должна обеспечивать мак - симальный средний выигрыш.
При выборе этой стратегии основой рассуждений является предположение, что противник является, по меньшей мере, так же разумен, как и мы сами, и делает все, чтобы добиться такой же цели.
Расчет на разумного противника лишь одна из возможных позиций в конфликте, но в теории игр именно она кладется в основу.
При этом для выбора оптимальной стратегии используют принцип максимина: выбирай ту стратегию, чтобы при наихудшем для нас поведении противника получить максимальный выигрыш. Другими словами, принцип максимина предполагает выбор той стратегии, при которой минимальный выигрыш для различных стратегий максимален. Отсюда и название «принцип максимина».
Как видно, принцип максимина - это принцип крайне осторожного игрока, но именно он является основным принципом теории матричных игр.
Для пояснения принципа максимина рассмотрим пример матричной игры G (4х5) с платежной матрицей, приведенной на рис. 2.2.

Рис. 2.2
Какой стратегией игроку А воспользоваться? Есть соблазнительный выигрыш 12, при применении стратегии А 3. Но при этом противник может выбрать стратегию В 3, и игрок А получит выигрыш, равный всего трем.
Для определения оптимальной стратегии в соответствии с принци- пом максимина, запишем в правом добавочном столбце платежной матри- цы минимальное значение A I в каждой строке (минимум строки). Из всех значений A I (правый столбец) выделим наибольшее. Ему соответствует стратегия А 4. Выбрав эту стратегию, мы во всяком случае можем быть уверены, что при любом поведении противника выигрыш будет не менее пяти. Эта величина - наш гарантированный выигрыш. Он называется нижней ценой игры (или «максимином» - максимальный из минимальных выигрышей). Будем обозначать его A. В нашем примере
a =  Aij =5.
Aij =5.
Игрока В выбирая стратегию должен рассчитывать на наихудшее для него поведение игрока А.
Припишем к платежной матрице (рис.2.2) нижнюю строку и в ней запишем наихудшее для игрока В возможные результаты (максимумы столб- цов B J).
Очевидно, осторожный противник должен выбрать стратегию, при которой величина B J минимальна. Эта величина называется верхней це- ной игры (или “минимаксом” - минимальный из максимальных проигры - шей). Будем обозначать ее B. В нашем примере
b =  Aij = 7.
Aij = 7.
Итак, исходя из принципа осторожности, игрок А должен выбрать стратегию А 4, а его противник - В 3. Такие стратегии называются максимин- ными или минимаксными стратегиями (вытекающие из принципа макси- мина).
До тех пор, пока обе стороны в нашем примере будут придержива- ться своих максиминных стратегий, выигрыш игрока А и проигрыш игро- ка В будет равен А 43 = 5.
Пример 2. Найти решение игры G (3х3), платежная матрица которой имеет следующий вид:
| Bj Ai | B1 | B2 | B3 | A I | |
| A1 | -1 | -2 | -2 | ||
| A2 | -1 | -1 | |||
| A3 | |||||
| Bj |
Определим 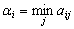 и
и  и запишем их в таблицу.
и запишем их в таблицу.
Нижняя цена игры 
Верхняя цена игры 
Так как a=b=0, то платежная матрица и матричная игра имеют седловую точку. Оптимальными стратегиями для игрока А является страте- гия А3, а для игрока В - В3.
Легко заметить, что отклонение игрока А от оптимальной стратегии приводит к уменьшению его выигрыша, а одностороннее отклонение игро- ка В - к увеличению его проигрыша.
Могут встречаться случаи, когда платежная матрица имеет несколь- ко седловых точек, однако это не изменит характера рекомендуемых реше- ний, поскольку все ситуации равновесия имеют одну и ту же цену, а следо- вательно, эквиваленты.
Теорема об активных стратегиях
Определение. Те из чистых стратегий игроков А и В, которые входят в их оптимальные смешанные стратегии с вероятностями, не равными нулю, называются активными стратегиями.
Если один из участников матричной игры G (M X N), придерживается своей оптимальной смешанной стратегии, то это обеспечивает ему максимальный средний выигрыш, равный цене игры n, независимо от того, какие действия предпринимает другой игрок, если только он не выходит за пределы своих активных стратегий (т. е. пользуется любой из них в чистом виде или смешивает их в любых пропорциях), причем число активных стратегий каждого игрока, входящих в их оптимальные смешанные стратегии, не превосходит L,
где L = min(m, n).
Применение теоремы об активных стратегиях позволяет упрощать решение некоторых матричных игр, в частности позволяет, упрощать решение матричных игр 2 x N и M x 2.
1.4 Методические рекомендации по решению матричной игры G (2x2)
Пусть задана матричная игра G (2x2) (см. рис.1)
 Bj
Ai Bj
Ai
| B1 | B2 |
| A1 | A11 | A12 |
| A2 | A21 | A22 |
Рис. 1 Матричная игра G (2x2)
Найти оптимальное решение данной матрицы
1.4.1 Решения задачи алгебраическим методом
В соответствии с основной теоремой игра имеет оптимальное реше- ние в смешанных стратегиях: SA = ||p1, p2|| и SB = ||q1, q2||, где вероят- ности применения (относительные частоты применения) чистых стратегий удовлетворяют соотношениям:
 ; (1)
; (1)
 .
.
В соответствии с теоремой об активных стратегиях, оптимальная смешанная стратегия обладает тем свойством, что обеспечивает игроку максимальный средний выигрыш, равный цене игры N, независимо от того, какие действия предпринимает другой игрок, если тот не выходит за преде- лы своих активных стратегий.
В частности, если игрок А использует свою оптимальную смешан- ную стратегию, а игрок В - свою чистую активную стратегию В1, то цена игры N равна
 , (2)
, (2)
а при использовании игроком В чистой активной стратегии В2, выигрыш будет равен
 . (3)
. (3)
Уравнения (1), (2) и (3) образуют систему трех линейных алгебраических уравнений с тремя неизвестным: p1, p2 и v.
Решая ее, легко находим, что
 . (4)
. (4)
 . (5)
. (5)
 . (6)
. (6)
Если игрок В использует свою оптимальную смешанную стратегию, а игрок А - свою чистую активную стратегию А1, то цена игры N равна
 , (7)
, (7)
а при использовании игроком А чистой активной стратегии А2, выигрыш будет равен
 . (8)
. (8)
Уравнения (2), (3), (7) и (8) образует систему трех линейных алгебраических уравнений с тремя неизвестными: q1; q2 и v. Решая ее, легко находим, что
 , (9)
, (9)
 , (10)
, (10)
 . (11)
. (11)
Естественно, что в обоих случаях цена игры (выражения (6) и (11)) получилась одна и та же.
1.4.2 Решение задачи графическим методом
Графический метод решения представлен на рис.2

Рис. 2 Графический метод
Для нахождения вероятностей p 1, p 2 и цены игры v в прямоугольной системе координат по оси абсцисс откладывается вероятность p 1Î [0,1], а по оси ординат - соответствующие этой вероятности выигрыши игрока А.
При р1=0, игрок А применяет чистую стратегию А 2. Если при этом игрок В применяет чистую стратегию В 1, то выигрыш игрока А равен а21, а если игрок В применяет чистую стратегию В 2, то выигрыш игрока А равен а22. При р1=1, игрок А применяет чистую стратегию А 1.
Если при этом игрок В применяет чистую стратегию В 1, то выигрыш игрока А равен а11, а при применении чистой стратегии В2 - а12. Так как значения р1 лежат в пределах [0,1], то соединяя крайние точки для стратегий В1 и В2 (строя графики функций vА = (a11 - a21)p1 + a22 и vА = (a12 - a22)p1+a22), получаем значения выигрышей игрока А для всех промежуточных значе - ний Р 1.
В соответствии с принципом максимина, игрок А должен выбрать такую смешанную стратегию, при которой его минимальный выигрыш максимален. Точка N пересечения отрезков прямых (рис. 2) и определяет как оптимальную цену игры v Opt, так и оптимальные вероятности p 1opt и p 2 opt =1- P 1opt, соответствующие оптимальной смешанной стратегии игрока А, т. е. дает решения системы уравнений (9), (10), (11).
Для графического решения системы уравнений (9), (10), (11) отложим по оси абсцисс вероятность q1Î [0,1], а по оси ординат соответствующие этой вероятности выигрыши игрока В:
vВ = (a11-a12)q1+a12; (12)
vВ = (a21-a22)q1+a22. (13)
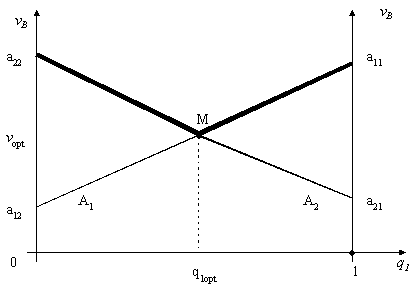
Рис. 3
Решением являются координат точки М пересечения прямых, описываемых уравнений (12) и (13):
q1opt;
q2opt=1- q1opt;
v Opt.
Это же следует и из принципа максимина, в соответствии с которым игрок В должен выбрать такую смешанную стратегию, при которой его максимальный проигрыш будет минимальным.