Графическая проверка передаточного отношения
1. Расчет радиусов колес планетарного редуктора:
,
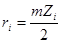где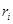 
- радиус iого колеса редуктора,
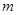- модуль.
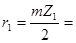18 мм
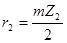= 36 мм
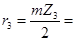13.5 мм
= 67.5 мм
2. Построение схемы планетарного редуктора в масштабе 
.
3. Построение диаграммы распределения линейных скоростей
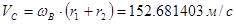
Выберем масштаб линейной скорости
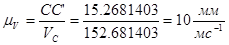
Для построения распределения линейных скоростей на схеме редуктора отметим характерные точки: центра колёс и точки зацепления, вынесем их на вертикальную ось радиусов.
Откладываем отрезок СС’. Строим линию распределения скоростей блока сателлитов – BA’. Строим OА’ - линия распределения скоростей 1 звена.
Строим отрезок AA’ выражающий в масштабе 
скорость точки A. Отрезок OC’ - линия распределения скоростей водила.
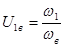=11,
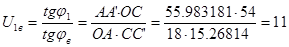
4. Построение диаграммы распределения угловых скоростей
Выберем масштаб угловой скорости:
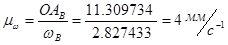
Для построения плана угловых скоростей проводим горизонтальную линию угловых скоростей. На ней откладываем отрезок OAB в масштабе 
=4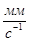 
.
Через точку AB проводим линию, параллельную линии ОАВ с диаграммы линейных скоростей. Точка пересечения с вертикальной осью, проходящей через т.О, является полюсом Р.
Проводим из полюса лучи, параллельные линиям распределения скоростей до пересечения с осью. Отрезки OAB, OC’, ОА’ выражают в масштабе угловые скорости водила, блока сателлитов и первого звена соответственно.
Вычислим передаточное отношение построенного планетарного редуктора:
.
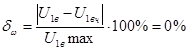Выводы
В результате расчета подобраны числа зубьев колес планетарного редуктора Z1=36; Z1=72; Z1=27; Z1=135, удовлетворяющие условиям сборки, соосности и соседства.
Был начерчен планетарный редуктор в масштабе, в 2-х проекциях в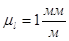 
.
|
|
Передаточное отношение проверено графически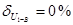 
.
Лист 3. Динамическое исследование основного механизма.
3.1. Исходные данные и постановка задачи:
| № п/п | Наименование параметра | Обозначения | Единица СИ | Числовое значение |
| Ход ползуна 5 | H5 | м | 0,5 | |
| Частота вращения кривошипа 1 | n1 | 1/с | 0,3 | |
| Коэффициент неравномерности вращения кривошипа 1 | d | - | 1/24 | |
| Коэффициент изменения средней скорости ползуна 5 | KV | - | 1,6 | |
| Отношение смещения e направляющей ползуна 5 к длине кривошипа 1 | le=e/l1 | - | 1.15 | |
| Отношение длины шатуна 4 к длине кулисы 3 | l43=l4/l3 | - | 0,25 | |
| Длина ползуна 5 в долях от его хода | l5=l5/H5 | - | ||
| Масса единицы длины ползуна 5 | Ml5/l5 | Кг/м | ||
| Масса единицы длины кулисы 3 | Ml3/l3 | Кг/м | ||
| Масса изделия И | mИ | кг | ||
| Коэффициент трения в направляющих ползуна 5 | fT56 | - | 0,24 | |
| Момент инерции кривошипа (коленчатого вала) | I1A | Кг*м2 | 0.06 |
Постановка задачи:
Провести геометрический синтез механизма.
Создать динамическую модель машинного агрегата
Определить движущий момент, необходимый при установившемся режиме на холостом ходу.
Получить закон движения главного вала машины
Рассчитать маховик.
3.2. Геометрический синтез механизма
1) 
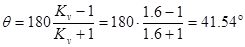
2) 
3) 
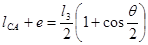, учитывая, что 
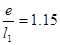и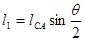 
получаем: 
= 
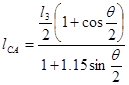4) 
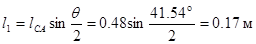
5) 
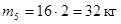
6) 
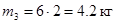
Для построения механизма выбираем масштаб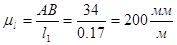 
. Произвольно выбираем место расположения шарнира A, проводим через точку A вертикальную прямую. Кроме того, проводим из т. A окружность радиусом АB. Разобьем окружность через равные углы на 12 частей 
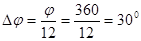. Строим механизм в 12 положениях (0-11) и в двух крайних положениях (2’,10’).
|
|
3.3. Создание динамической модели
Для того чтобы упростить определение закона движения сложной системы, реальный механизм заменяют динамической моделью. Модель представляет собой стойку и вращающееся звено, называемое звеном приведения, инерционность которого определяется суммарным приведенным моментом инерции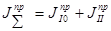 
. На звено приведения действует суммарный приведенный момент сил 
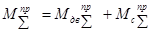. Параметры динамической модели 
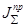и 
определяют так, чтобы законы движения звена приведения динамической модели и движения начального звена реального механизма совпадали: 
; 
.
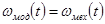В качестве начального звена механизма выбран кривошип 1. Таким образом, обобщенная координата для механизма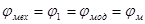 
. 
и 
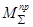определяются методом приведения сил и масс.
Определение суммарного приведенного момента
Метод приведения сил основан на равенстве элементарных работ и мгновенных мощностей приведенного момента, приложенного к модели, и реальных сил – к реальному механизму.
Для модели мощность 
, где 
, а для реального механизма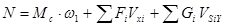 
, где 
- проекции на вертикаль скорости центра масс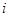 
-го звена.
Nмод=Nмех
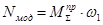
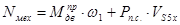
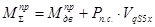
3.3.2 Определение суммарного приведенного момента инерции
Метод приведения масс и моментов инерции основан на равенстве кинетической энергии звена приведения динамической модели и кинетической энергии реального механизма в каждый момент времени.
Tмод=Tмех
,
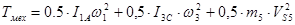
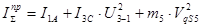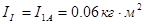
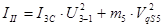
3.4 Передаточные функции