Рассчитаем силы полезного сопротивления:
На рабочем ходу: звено 5 двигается вместе с изделием, значит 
На холостом ходу: 
Рассчитаем  для положения 1:
для положения 1:

Остальные значения  запишем в таблицу 5
запишем в таблицу 5
Таблица 5
Значения приведённых моментов.
| Приведённый момент | Положения механизма | |||||||||||||
| 2' | 10' | |||||||||||||

| -29.749 | -18.572 | -3.76 | -9.593 | -17.427 | -21.414 | -23.033 | -21.998 | -17.429 | -7.79 | -3.235 | -18.618 |
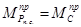
Далее строим график изменения момента 
Выбираем масштаб 
Вычислим масштаб  :
:

3.6 Построение графика работ.
Проинтегрируем график  и получим график
и получим график  . Его масштаб определяется по формуле:
. Его масштаб определяется по формуле:
 ,
,
где  - масштаб работы,
- масштаб работы, 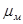 и
и  – масштабы по осям координат графика приведенного движущего момента,
– масштабы по осям координат графика приведенного движущего момента,  - отрезок интегрирования.
- отрезок интегрирования.
В данном случае приведенный момент  равен действительному моменту
равен действительному моменту  , т. к. последний приложен к входящему звену и в первом приближении его можно считать постоянным. Однако величина
, т. к. последний приложен к входящему звену и в первом приближении его можно считать постоянным. Однако величина  определяется из условия, что
определяется из условия, что  . Конечная ордината графика
. Конечная ордината графика  должна быть равна
должна быть равна  для установившегося режима движения и с учетом того, что
для установившегося режима движения и с учетом того, что  , строится график
, строится график  в виде наклонной прямой линии. Дальнейшим графическим дифференцированием графика
в виде наклонной прямой линии. Дальнейшим графическим дифференцированием графика  определяем величину
определяем величину  .
.
 , с другой стороны:
, с другой стороны:

Погрешность: 
Сложим график работ движущей силы  за цикл и работы сил сопротивления
за цикл и работы сил сопротивления  за цикл, получим график суммарной работы.
за цикл, получим график суммарной работы.
3.7 Определение приведенного момента инерции второй группы звеньев 
Подсчитаем значение  для механизма в положении 0:
для механизма в положении 0:

Значения  для всех остальных положений механизма сведем в таблицу 6:
для всех остальных положений механизма сведем в таблицу 6:
Таблица 6
Значения моментов инерции.
| Момент инерции | Положения механизма | |||||||||||||
| 2' | 10' | |||||||||||||
| I3 | 0.21 | 0.087 | 0.003 | 0.009 | 0.029 | 0.043 | 0.048 | 0.043 | 0.029 | 0.009 | 0.003 | 0.087 | ||
| I5 | 5.102 | 1.988 | 0.082 | 0.2 | 0.663 | 1.001 | 1.158 | 1.056 | 0.663 | 0.132 | 0.06 | 1.998 | ||
| I_IIгр | 5.312 | 2.076 | 0.085 | 0.21 | 0.692 | 1.044 | 1.206 | 1.099 | 0.692 | 0.141 | 0.063 | 2.086 |
По данным таблицы строим график  в масштабе
в масштабе  :
:

График  может быть приближенно принят за график кинетической энергии второй группы звеньев
может быть приближенно принят за график кинетической энергии второй группы звеньев  . Действительно:
. Действительно:  .
.
Закон изменения  еще не известен. Поэтому для определения
еще не известен. Поэтому для определения 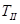 приближенно принимаем
приближенно принимаем  , что возможно, т.к. величина коэффициента неравномерности
, что возможно, т.к. величина коэффициента неравномерности  величина малая и, тогда величину
величина малая и, тогда величину  можно считать пропорциональной
можно считать пропорциональной  , а построенную кривую можно принять за приближенную кривую
, а построенную кривую можно принять за приближенную кривую  . Масштаб графика
. Масштаб графика  :
: 
3.8 Построение приближенного графика 
Известно, что  . С другой стороны
. С другой стороны 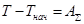 , т.е. кинетическая энергия механизма отличается от
, т.е. кинетическая энергия механизма отличается от  на некоторую постоянную величину
на некоторую постоянную величину  . Поэтому ранее построенный график
. Поэтому ранее построенный график  можно принять за график
можно принять за график  относительно оси
относительно оси  , отстоящей от оси
, отстоящей от оси  на величину
на величину  . следовательно для построения кривой
. следовательно для построения кривой  необходимо из ординат кривой
необходимо из ординат кривой  в каждом положении механизма вычесть ординаты графика
в каждом положении механизма вычесть ординаты графика  , взятые в масштабе
, взятые в масштабе  , в каком построена кривая
, в каком построена кривая  :
: 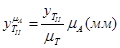 .
.
Полученная кривая  приближенная, т.к. построена вычитанием из точной кривой
приближенная, т.к. построена вычитанием из точной кривой  приближенных значений
приближенных значений  .
.
На кривой  находят
находят  и
и  , и определяют максимальное изменение кинетической энергии I группы звеньев за период одного цикла:
, и определяют максимальное изменение кинетической энергии I группы звеньев за период одного цикла:
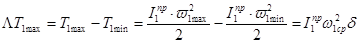 , откуда
, откуда

3.9 Определение закона движения начального звена механизма
Максимальному значению  соответствует
соответствует  , а
, а  соответствует
соответствует  , т.к.
, т.к.  . Поэтому
. Поэтому  будет соответствовать
будет соответствовать  в масштабе
в масштабе  . Чтобы определить график
. Чтобы определить график  , необходимо найти положение оси абсцисс
, необходимо найти положение оси абсцисс  . Для этого через середину отрезка
. Для этого через середину отрезка  , проводят линию, которая является средней угловой скоростью
, проводят линию, которая является средней угловой скоростью  . Рассчитаем графическую величину
. Рассчитаем графическую величину  . Определим коэффициент неравномерности вращения:
. Определим коэффициент неравномерности вращения: 
Определим погрешность 
3.10 Геометрический расчет маховика.
Определим момент инерции дополнительной маховой массы





предположим что  , тогда
, тогда 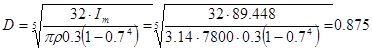 м
м

Чертим маховик в масштабе 
Вывод:
· Провели геометрический синтез механизма, определили:






· Создали динамическую модель, с параметрами:




· Подобраны размеры маховика:



· Создан закон движения ω(φ)
Определим угловую скорость и ускорение, при φ=60О:
ω1= ωср+Δy/μω=1.88+1.018 /89.98= 1,891 c-1
ε1= ω1*tgψ*μφ/μω=1.891*tg(18.63)*19.1/89.98= 0,135c-2