В 2001 квантовый компьютер на 7 кубитах с помощью этого алгоритма смог разложить 15 на 3×5. (Наибольшее число, разложенное на квантовом устройстве = 56153 — 2014 год, но не Шором, а адиабатическое вычисление)
Алгоритм состоит из двух частей:
1. классическая часть - свести задачу к нахождению периода функции.
2. квантовая часть — найти период.
Классическая часть:
1. берём произвольное число a < N.
2. вычисляем НОД(a,N) (наибольший общий делитель). Например, с помощью алгоритма Эвклида — вычитаем из большего числа меньшее.
3. Если НОД(a,N)≠1, то нетривиальный множитель найден, конец.
4. В противном случае, с помощью квантового алгоритма, основанного на дискретном преобразовании Фурье, находим период функции 
, т. е. такое целое число r, что 
5. если r нечётное, или a r /2≡ −1 (mod N) - возвращаемся к шагу 1.
6. НОД(ar /2+ 1, N) и НОД(ar /2- 1, N) — нетривиальные множители N. Конец.
Например: 
. 
, где
и 
(Примечание: самый быстрый классический алгоритм решения этой задачи — квадратичное решето — основан на той же идее. Но медленнее, т. к. задача поиска порядка функции тяжело решается классическим компьютером)
Квантовая часть:
Квантовая цепочка создаётся каждый раз отдельно для каждого N, и каждого случайного выбора a.
Находим некоторое Q = 2 q,такое что 
, что означает 
.
Вход и выход будут содержать суперпозиции состояний от 0 до Q − 1, поэтому состоят из q кубитов. 
1. Создаём суперпозицию всех состояний — с помощью вентилей Адамара, или к. преобразования Фурье
2. Конструируем f (x) как к. функцию, и применяем к состоянию выше 
(Шор использовал алгоритм быстрого возведения в степень, чтобы достичь этого. Это самый долгий шаг. Он заметно сложнее, чем QFT – нужно много вентилей. По сути, он имитирует классический обратимый алгоритм для этой задачи)
3. Применяем к. преобразование Фурье ко входу. 
(Шор использовал для реализации QFT вентили фазового сдвига и вентили Адамара)
(Вентиль Адамара: переводит n кубитов, инициализированных в |0>, в суперпозицию всех 2 n ортогональных состояний в базисе (|0>,|1>) с равными весами) 
Q FT использует Qтый комплексный корень единицы: 
, чтобы равномерно распределить амплитуду любого данного состояния |x> между всеми Q для состояния |y> - и делать это по-разному для каждого |x>.
В результате приходим к состоянию 
, или если записать иначе: 
Возьмём x 0- наименьший x, что f (x) = z (x 0< r), и b — индексирует эти x, пробегая от 0 до (Q- x0-1)/r, так что x0+rb<Q. Тогда получим:
Каждое слагаемое в этой сумме даёт разные пути к одной цели — и возникает к. интерференция: амплитуды состояний, для которых единичные векторы 
направлены практически в одну сторону (что значит что вектор 
направлен вдоль положительной вещественной оси), усиливаются; остальные ослабевают.
4. Производим измерение, и получаем y на входе, и z на выходе. Вероятность получить данные y и z тем выше, чем ближе к положительной вещественной оси, или чем ближе yr/Q к целому числу.
5. Т.к. yr/Q близко к некоторому целому c, то 
известное значение y / Q близко к неизвестному c / r. Осуществив (классически) непрерывную дробную последовательность, мы найдём такие аппроксимации d/s, что:
· s<N
· |y/Q - d/s| < 1/2Q.
Если d / s не упрощаемая дробь, то s — весьма вероятно наш искомый период r.
6. Проверяем (классически), что 
. Если да, то конец. Иначе, пробуем прогнать всю эту часть ещё раз.
Говоря просто, алгоритм Шора разбивает задачу на Q состояний, каждое из которых — один из возможных r – периодов функции. И затем, благодаря к. спутанности и интерференции, вычисление производится по всем путям одновременно (по сути, это аналог алгоритма к. оценки фазы: вследствие интерференции, амплитуды состояний вдоль перспективных путей стремительно растут, остальные стремительно падают). Отсюда к. выигрыш в скорости.
Также алгоритм Шора может использоваться для нахождения дискретного логарифма.
2) Алгоритм Гровера (Leo Grover, 1996) — найти х по заданному у, такой что f(x)=y. Это, по сути, алгоритм инвертирования функции — но он может быть и переформулирован как алгоритм поиска по базе данных (f(x) тогда будет функцией, возвращающей 1 для искомого х, и 0 для всех остальных). В общем виде, f(x) - это чёрный ящик, или оракул, как-то отвечающий на запрос «да» или «нет».
Алгоритм Гровера работает за время O(N 1/2), где N – размер области определения f(x). Классический алгоритм не может решить этой проблемы за время меньше O(N). И доказано, что O(N 1/2) — наименьшее возможное время для любого квантового алгоритма решения, т.е. алгоритм Гровера — оптимальный.
На практике, этот алгоритм тоже можно использовать для взлома 128-битного криптографического ключа - методом перебора за 264итераций. Т.е., алгоритм Гровера даёт не экспоненциальное ускорение, по сравнению с классическим (как другие квантовые алгоритмы, применимые в более специфических случаях) — а лишь квадратичное. Но и то неплохо.
Алгоритм — вероятностный, т. е. даёт правильный ответ с вероятностью <1. Но предполагается, что количество повторов, чтобы приблизить вероятность к 1 — это постоянная величина, и не зависит от N.
Описание:
Алгоритм работает на N-мерном пространстве состояний H - для которого надо n =log2 N кубитов. У нас есть унитарный оператор Uω, который зеркально отражает вектор состояния относительно гиперплоскости, перпендикулярной ω.
Мы начинаем с состояния 
- равномерной суперпозиции всех возможных состояний величин x:
Тогда 
, Осуществляем «гроверовскую итерацию» r(N) раз (
):
1. Применяем оператор 
.
2. Применяем оператор 
.
Осуществляем измерение, и получаем искомую ω с вероятностью, стремящейся к 1.
Геометрическое объяснение:
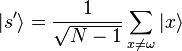
- кет, перпендикулярный 
:
Оператор 
- это, по сути, отражение вектора по отношению к . Оператор - это отражение по отношению к . Таким образом, каждая итерация алгоритма (т. е. применение оператора 
) поворачивает его вектор состояния на угол 
.
Нам нужно остановиться, когда вектор состояния подойдёт достаточно близко к ; дальнейшие итерации будут удалять вектор состояния от , снижая вероятность правильного ответа. Вероятность измерения правильного ответа будет 
, где r — это количество гроверовских итераций.
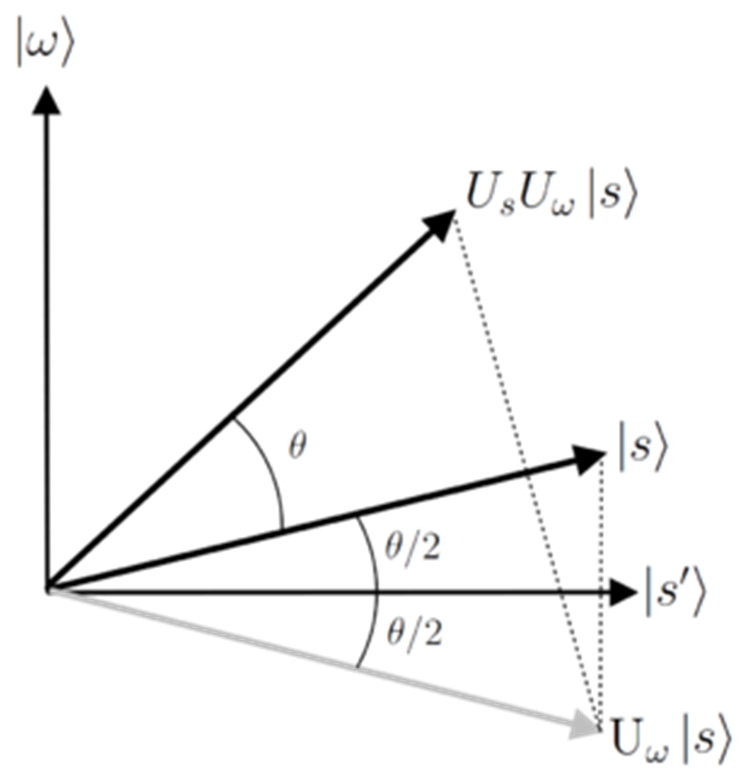Смысл GSA состоит в «подскоке амплитуды» (amplitude amplification) целевого состояния за счёт убывания амплитуды всех других состояний.
На практике, в 2012м, реализовали алгоритм Гровера для четырёх вариантов перебора.
