18) Напряжение изгиба в опасных сечениях на переходных поверхностях зубьев шестерни и колеса
где bw – ширина венца зубчатого колеса(b2 = b3 = 36 мм);
– коэффициент, учитывающий форму зуба. При X2 = 0 и числе зубьев эквивалентного колеса Zv2 = 26 YF2 = 3,8. При X3 = 0 и числе зубьев эквивалентного колеса Zv3 = 242 YF3 = 3,6.
– коэффициент, учитывающий влияние перекрытия зубьев. Для прямозубых передач 
.
KF – коэффициент нагрузки при расчёте на изгиб.
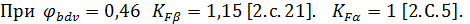
19) Допускаемое напряжение изгиба не взывающее усталостной поломки зуба:
где 
– базовый предел изгибной выносливости, МПа;
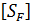– минимальный коэффициент запаса прочности при изгибе;
– коэффициент долговечности при изгибе;
– коэффициент, учитывающий шероховатость переходной поверхности;
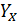– коэффициент, учитывающий размеры зубчатого колеса;
– коэффициент, учитывающий влияние двустороннего приложения нагрузки;
– коэффициент, учитывающий способ получения заготовки зубчатого колеса;
– коэффициент, учитывающий влияние шлифования переходной поверхности зубьев;
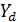– коэффициент, учитывающий влияние деформационного упрочнения переходной поверхности.
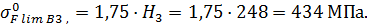
для стальных колёс с нешлифованной переходной поверхностью.
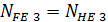при постоянном режиме нагружения, так как
, если переходная поверхность не шлифуется.
, если переходная поверхность не подвергается деформационному упрочнению.
20) Проверка сопротивления зубьев усталости при изгибе
Сопротивление зубьев усталости при изгибе обеспечивается. Усталостной поломки зубьев в пределах расчётного срока службы не будет.
3.2 Расчет цилиндрической косозубой зубчатой передачи тихоходной ступени.
Исходные данные:
– Вращающий момент на меньшем колесе Т4 = 130,83 Н·м.
– Частота вращения меньшего колеса nII = 469,35 об/мин.
– Передаточное число зубчатой передачи U = 3,9.
– Требуемый ресурс передачи Lh = 9216ч.
– Делительный угол наклона линии зуба β = 21˚.
– Режим нагружения постоянный.
– Производство единичное.
Проектировочный расчёт из условия сопротивления контактной усталости поверхностей зубьев:
1) Задаём материал и твёрдости рабочих поверхностей зубьев.
Материал шестерни и колеса: сталь 45, термообработка“улучшение”.
Твердость шестерни H4 = 285 HB, колеса H5 = 248 HB.
2) Определяем допускаемые контактные напряжения, не вызывающие опасной контактной усталости материалов колес:
где σ H lim B – базовый предел контактной выносливости материалов зубьев, МПа;
ZN – коэффициент долговечности;
[SH] – минимальный коэффициент запаса прочности;
ZR – коэффициент, учитывающий влияния исходной шероховатости сопряжённых поверхностей зубьев;
ZV – коэффициент, учитывающий влияние окружной скорости колёс;
ZX – коэффициент, учитывающий размеры зубчатых колёс.
σ H lim b4 = 2H4 + 70= 2 · 285 + 70 = 640 МПа.
σ H lim b5 = 2H5 + 70= 2 · 248 + 70 = 566 МПа.
[SH]4,5 = 1,1 – при термообработке “улучшение”.
где NHlimB – базовое число циклов напряжений;
NHE – эквивалентное число циклов изменения контактных напряжений;
qH – показатель степени кривой усталости.
NHlimB4 = 30 · H42,4 = 30 · 2852,4 = 23,4 · 106 циклов;
NHlimB5 = 30 · H52,4 = 30 · 2482,4 = 16,7 · 106 циклов;
NHE = 60 · Lh · n · j · μH,
где j – число вхождений рассчитываемой стороны зуба в зацепление за один оборот колеса;
μH – коэффициент, учитывающий форму циклограммы нагружения. При постоянном режиме нагружения μH = 1.
NHE4 = 60 · Lh · n4 · j4 · μH = 60 · 9216 · 469,35 · 1 · 1 = 259,5 · 106 циклов;
NHE5 = 60 · Lh · n5 · j5 · μH = 60 · 9216 · 120,34· 1 · 1 = 66,5 · 106 циклов;
Так как NHE4,5 > NHlimB4,5 qH = 20
ZR · Zv · Zx = 0.9– на этапе проектного расчёта.
Расчётное допускаемое контактное напряжение для косозубых колёс:
[σН]Р = 0,45([σН]4 + [σН]5 ) = 0,45(464,25+432,21) =403,412МПа.
Так как [σН]р вышел за пределы (1..1,23) ·[σН]4, принимаем [σН]р = 432,21 МПа
3) Определяем ориентировочное значение межосевого расстояния передачи:
где Ка – вспомогательный коэффициент;
КHβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий;
– предварительное значение коэффициента ширины венца относительно межосевого расстояния.
где 
– предварительное значение коэффициента ширины венца относительно диаметра.
При симметричном относительно опор расположении колёс и H4,5 < 350HB, задаёмся 
; 
КHβ = 1,03
Проверяем отсутствие подрезания зубьев колёс:
где X – коэффициент смещения исходного контура.
αt – делительный угол профиля зубьев в торцевом сечении.
где α = 20 – угол профиля исходного контура
Так как Z4 и Z5 > Zmin, подрезания зубьев колёс не будет.
5) Уточнённое значение передаточного числа:
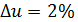
6) Делительный нормальный модуль зубьев:
7) Округляем модуль до стандартного: m = 3 мм.
8) Межосевое расстояние передачи при стандартном модуле зубьев:
9) Уточнённое значение коэффициента ширины венца:
10) Рабочая ширина венца зубчатой передачи:
11) Геометрические и кинематические параметры колеса:
- делительные диаметры
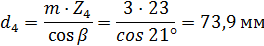
- начальные диаметры
- диаметры впадин
- диаметры вершин
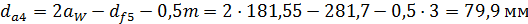
- коэффициент торцевого перекрытия:
- осевой шаг зубьев
- коэффициент осевого перекрытия:
- суммарный коэффициент перекрытия:
- основной угол наклона линии зуба:
- окружная скорость колеса на начальных цилиндрах:
12) Назначаем степень точности передачи 8, так как
V4= V5=1,81 м/с не больше 10 м/с