Системы координат, используемые для определения параметров движения РН.
Начальная стартовая система координат – система с центром в точке старта (О). при этом ось Y направлена по местной вертикали, ось Х расположена в плоскости выведения и направлена в сторону полета ракеты, перпендикулярно оси Y ось Z дополняет систему до правой. ИНКС определяется на момент времени t˳
5. Структура аналоговой СУ РН, реализующей метод жесткого программирования.
В соответствии с рассмотренными задачами СУД ракеты состоит из двух основных систем: системы наведения (СН) и системы стабилизации (СС). Её типовая структура может быть представлена в виде, показанном на рис. 2.2.
На рис.2.2 обозначено:
– вектор параметров движения (или иначе, вектор состояния, вектор фазовых координат);
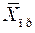– его программное значение, вычисленное системой наведения в соответствии с полётным заданием 
;
– вектор отклонений управляющих органов (УО), создающих управляющие воздействия на ракету;
t к – команда на выключение ДУ.
Система наведения (СН) и система стабилизации (СС) находятся в тесном взаимодействии: СН определяет требуемое (программное) движение ракеты, а СС его реализует. В состав каждой системы, как отмечалось ранее, входят соответствующие ИзмУ, УФСУ, ИУ.
Помимо рассмотренных СН и СС в состав бортовой СУ входят и другие системы, не участвующие непосредственно в управлении движением, но обеспечивающие необходимые условия и требуемое качество функционирования СУД. Среди этих систем необходимо отметить систему опорожнения баков (СОБ), которую в последнее время чаще называют системой управления расходом топлива (СУРТ), систему электроснабжения (СЭС), систему безопасности носителя (СБН) и др.
Метод жёсткого программирования базируется на наличии априорной информации об условиях движения ракеты (т.е. силы и моменты, действующие на ракету в полёте, полагаются известными), которая позволяет рассчитать программу движения и отвечающую ей программу управления заранее и ввести последнюю в СУ
Структура СУ с БЦВМ, реализующий метод ИТН (на примере РН «Зенит»).
При наличии в СУ БЦВМ задача формирования программы, естественно, возлагается на неё. В таких случаях обычно используются параметрические программы, например, вида 
. Характерный вид этой зависимости (для случая БР) показан на рис. 2.6.
Для воспроизведения этой зависимости используется её кусочно-квадратичная аппроксимация выражением:
= am+bmVsy+cm 
,
где am, bm, cm – коэффициенты, постоянные для участка,
m – номер участка аппроксимации.
На этапе выведения программа обычно содержит четыре участка, длина которых задаётся значениями скорости Vsym . Значения коэффициентов представляются таблицей 2.1.
Коэффициенты a 2, b 2, a 3, b 3, c 3, a 4, а также Vsуm зависят от условий стрельбы, рассчитываются заранее и вводятся в СУ (в память БЦВМ) в составе полётного задания.
Результаты вычислений по приведённой выше формуле образуются в БЦВМ в виде двоичного кода, который используется в самой БЦВМ для сравнения с кодом, соответствующим измеренному с помощью ИзмУт фактическому значению угла тангажа 
, с целью вычисления рассогласования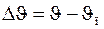 
.
Таблица 2.1
| am | bm | cm | |
| I | π/2 | ||
| II | a 2 | b 2 | |
| III | a 3 | b 3 | c 3 |
| IV | a 4= к
|