СОДЕРЖАНИЕ
ЗАДАЧА 1. СЕЛЬСКОЕ ХОЗЯЙСТВО………………….……………....4
1.1 Задание……………………………………………………………...….4
1.2 Оптимальное решение…………………………………….....…….….5
1.3 Отчет о результатах………………………………..……………….…6
1.4 Отчет об устойчивости…..………………………………..……….….6
1.5 Ответы на вопросы задания………………………..………..……..…7
ЗАДАЧА 2. ПРОИЗВОДСТВО…………………………………....….…..8
2.1 Задание……………...……………………………….….………….…...8
2.2 Оптимальное решение……………………..………………….…...….9
2.3 Отчет о результатах………………...……………………….………..10
2.4 Отчет об устойчивости……………...……………………..…………10
2.5 Ответы на вопросы задания………………………...………..………11
ЗАДАЧА 3. ИЗГОТОВЛЕНИЕ И ДОСТАВКА……………………...…12
3.1 Задание……….…………...………………………………………..….12
3.2 Оптимальное решение………………...……………………………...13
3.3 Отчет о результатах……………..………………………….………...14
3.4 Отчет об устойчивости.........................................................................15
3.5 Ответы на вопросы задания…………………..……………..….……16
ЗАДАЧА 4. ТОРГИ.....................................................................................17
4.1 Задание...................................................................................................17
4.2 Оптимальное решение..........................................................................18
4.3 Отчет о результатах..............................................................................19
4.4 Ответ на вопросы задания....................................................................21
СПИСОК ЛИТЕРАТУРЫ…………………………………………….….22
Задача 1. сельское хозяйство
Задание
У вас — ферма и 800 гектаров орошаемой земли. Вы выращиваете пшеницу и люцерну, а также скот для продажи. Для полива земли в следующем году вам выделено местными властями 1000 единиц расхода воды (1 ед. – 1000 куб. м). Составляя производственный план на будущий год, вы прикинули, что в следующем году цена говядины составит примерно 500 денежных единиц за тонну, пшеницы — 2 ден. ед. за единицу объема, люцерны — 22 ден. ед. за тонну. Для откорма скота используется выращенная люцерна, и если окажется, что ее не хватит, то придется докупать люцерну по цене 28 ден. ед. за тонну.
Обычно урожай пшеницы составляет 70 единиц объема с гектара, люцерны — 4 тонны с гектара. Другие данные приведены в следующей таблице.
Таблица 1 – сельское хозяйство
| Вид деятельности | Затраты на труд, машины и др. (ден. ед.) | Расход воды (ед. расхода воды) | Расход земли (гектары) | Расход люцерны (тонны) |
| 1 гектар пшеницы | 1,429 | 0,535 | 0,517 | |
| 1 гектар люцерны | 2,000 | 0,802 | 0,517 | |
| 1 тонна говядины | 3,571 | 0,013 | 0,052 | 5,000 |
Вы хотите составить оптимальный план своей деятельности на будущий год.
Рекомендации
При моделировании переменные определены следующим образом:
x 1 — количество выращенной и проданной пшеницы (гектары);
x 2 — количество выращенной люцерны (тонны);
x 3 — количество произведенной и проданной говядины (тонны);
x 4 — количество купленной люцерны (тонны);
x 5 — количество проданной люцерны (тонны).
138,6 x 1 – 0,5 x 2 + 496,4 x 3 – 28 x 4 + 22 x 5 ® max (максимизация прибыли)
0,52x 1 + 0,13 x 2 + 0,05 x 3 ≤ 800 (ограничение на площадь используемой земли)
0,53 x 1 + 0,80x 2 + 0,01 x 3 ≤ 1000 (ограничение на расход воды)
x 2 – 5 x 3 + x 4 – x 5 = 0 (условие баланса: общий объем выращенной и купленной люцерны равен объему люцерны, скормленной скоту и проданной)
x 1, x 2, x 3, x 4, x 5 ≥ 0
Оптимальное решение

Рисунок 1 - Решение

Рисунок 2 - Используемые формулы
138,6 x 1 – 0,5 x 2 + 496,4 x 3 – 28 x 4 + 22 x 5 ® max (максимизация прибыли)
x 1 = 0 (количество выращенной и проданной пшеницы (гектары));
x 2 = 0 (количество выращенной люцерны (тонны));
x 3 = 15474,69 (количество произведенной и проданной говядины (тонны));
x 4 = 77373,46(количество купленной люцерны (тонны));
x 5 = 0 (количество проданной люцерны (тонны)).
При оптимальном управлении прибыль равна 5515622,136 ден. ед.
Отчет о результатах
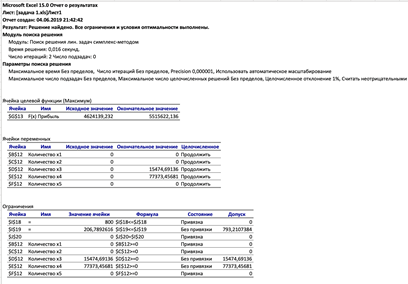
Рисунок 3 - Отчет о результатах
Отчет об устойчивости

Рисунок 4 – Отчет об устойчивости
1.5 Ответы на вопросы задачи
1. Коэффициент переменной в целевой функции:
x 1= 70*2-1,43, (Урожай пшеницы * цена пшеницы – затраты на труд на пшеницу) коэффициенты переменной в ограничениях x 2. = (0,517 )*0,25 (Расход земли на люцерну* 0,25 (т.к. x 2 в тоннах))
х3. = (500 – 3,571) (Цена говядины – затраты на труд, машины и др.)
2. Будет израсходовано 0 единиц воды
3. Будет произведено и продано 15474,69 тонн говядины
4. Люцерна не будет продана, но будет куплена в размере 77373,46 тонн.
5. Если цена пшеницы утроится, то коэффициент переменной в целевой функции станет равным 418,6. Значение целевой функции не изменится, так как мы не производим пшеницу.
6. При оптимальном управлении фермой мы сможем получить прибыль в размере 5515622,136 ден. ед.
7. Если цена закупаемой люцерны возрастет с 28 до 29 ден. ед., оптимальное значение целевой функции станет равным 5438248,679.
8. Так как оптимальный план напрямую зависит от цены закупаемой люцерны, любое изменение в цене повлияет на значение оптимального плана.
ЗАДАЧА 2. ПРОИЗВОДСТВО
Задание
Вы обрабатываете два продукта A и B на трех станках. При этом можно использовать два технологических способа. Первый предусматривает обработку продуктов на 1-м и 2-м станках, а второй — на 1-м и 3-м. Время обработки указано в следующей таблице.
Таблица 2 - Производство
| Продукт | Способ | Машинное время (ч/шт.) | ||
| Станок 1 | Станок 2 | Станок 3 | ||
| A | 0,14 | 0,27 | ||
| A | 0,14 | 0,78 | ||
| B | 0,07 | 0,53 | ||
| B | 0,07 | 1,55 |
Стоимость одного часа работы 1, 2 и 3-го станков составляет 20, 30 и 18 рублей, соответственно. Каждый из них может работать 40 ч в неделю. Любое количество продуктов A и B может быть продано по цене 110 и 150 рублей, соответственно.
Вы хотите составить оптимальный производственный план.
Рекомендации
При моделировании переменные определены следующим образом:
Ai — количество продуктов A, производимых способом i (i = 1, 2);
Bi — количество продуктов B, производимых способом i (i = 1, 2);
Тогда математическая модель будет выглядеть следующим образом:
99,13 A 1 + 93,18 A 2 + 132,54 B 1 + 120,65 B 2 ® max
0,14 A 1 + 0,14 A 2 +0,07 B 1 + 0,07 B 2 ≤ 40
0,27A 1 +0,53 B 1 ≤ 40
0,78 A 2 + 1,55 B 2 ≤ 40
A 1, A 2, B 1, B 2 ≥ 0
Анализируя эту модель, имейте в виду, что при вычислении прибыли в целевой функции учитываются как выручка, так и издержки.
Оптимальное решение

Рисунок 5 - Решение

Рисунок 6 - Используемые формулы
99,13 A 1 + 93,18 A 2 + 132,54 B 1 + 120,65 B 2 ® max
A1 = 149,66;
A2 = 51,58;
В1 = 0;
B2 = 0;
При оптимальном управлении прибыль равна 19642,35 ден. ед.
Отчет о результатах

Рисунок 7 – Отчет о результатах
Отчет об устойчивости

Рисунок 8 – Отчет об устойчивости
2.5 Ответы на вопросы задания
1. A 1 = 110-(20*0,14+30*0,27) = 99,13
A 2 = 110-(20*0,14+18*0,78) = 93,18
B 1 = 150-(20*0,07+30*0,53) =132,54
B 2 = 150-(20*0,07+18*1,55) = 120,65
2. В продуктов будет выпущено 0. Их производить не нужно
3. 1 станок будет работать 28,7498 ч
2 станок будет работать 40ч
3 станок будет работать 40ч
4. Есть возможность сверхурочной работы в течение 8 ч на 2-ом станке стоимостью 45 рублей в час (на 50% больше, чем обычная стоимость — 30 рублей в час). Стоит ли включить в план сверхурочные 8 ч работы на 2-м станке? Стоит включать в план сверхурочные работы, так как благодаря этому повысится прибыль предприятия
ЗАДАЧА 3. ИЗГОТОВЛЕНИЕ И ДОСТАВКА
Задание
Вы фасуете экзотические фрукты в красивую упаковку для использования в качестве праздничных подарков. Фасовка происходит в двух пунктах, откуда упакованные фрукты отправляются пяти оптовым торговцам. Затраты на изготовление одной упаковки в 1-м и 2-м пунктах составляют 5,25 и 5,70 рублей, соответственно. Вы прогнозируете, что количество упаковок, которое потребуется оптовым торговцам, будет следующим.
Таблица 3 – Поставки требуемым торговцам
| Оптовый торговец | |||||
| Требуемая поставка | 10 000 |
Производственные мощности пунктов фасовки позволяют на 1-м из них изготовить 20 000 упаковок, а на 2-м — 12 000. В следующей таблице показано, во сколько обходится доставка одной упаковки из каждого пункта фасовки каждому оптовому торговцу (в рублях).
Таблица 4 – Цены на поставки
| Из пункта | Оптовые торговцы | ||||
| 0,04 | 0,11 | 0,62 | 0,90 | 0,19 | |
| 0,11 | 0,24 | 0,50 | 0,41 | 0,80 |
Вы хотите составить оптимальный план поставки своего товара оптовым торговцам.
Рекомендации
Сформулируйте модель как транспортную задачу линейного программирования. При построении целевой функции учитывайте затраты не только на доставку товара, но и на его изготовление.
Оптимальное решение
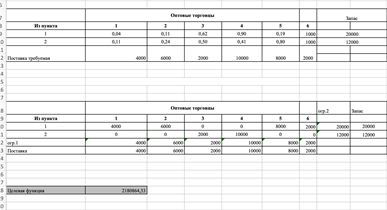
Рисунок 9 - Решение

Рисунок 10 - Используемые формулы
Отчет о результатах

Рисунок 11 – Отчет о результатах

Рисунок 12 – Отчет о результатах продолжение
Отчет об устойчивости
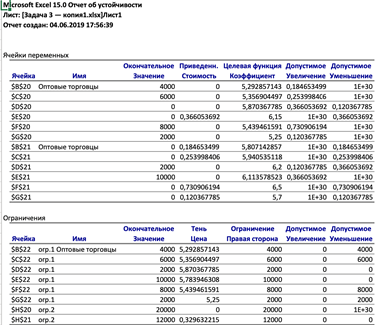
Рисунок 13 – Отчет об устойчивости
3.5 Ответы на вопросы задания
1. 1 торговцу следует направить 4000 упаковок из 1 пункта
2 торговцу следует направить 6000 упаковок из 1 пункта
3 торговцу следует направить 2000 упаковок из 2 пункта
4 торговцу следует направить 10000 упаковок из 2 пункта
5 торговцу следует направить 8000 упаковок из 1 пункта
2. Минимальные издержки будут равны 2180864,3335
При этом 2000 единиц продукции будут оставаться в пункте 1(так оправляются фиктивному пунктом). Минимальные издержки при таком плане составляют 2180864,3335, а фактически(за вычетом издержек фиктивного торговца) равны 2180864,3335-2000*1000=180864,3335
3. Нужно уменьшить на такую величину, чтобы стоимость доставки была меньше той, которая выбрана нами по исходным данным. То есть, для 1 оптового торговца стоимость доставки к пункту 2 должна быть ниже 0,07 (0,11-0,04), для 2 оптового торговца стоимость доставки к пункту 2 должна быть ниже 0,13, для 3 оптового торговца стоимость доставки к пункту 1 должна быть ниже 0,12, для 4 оптового торговца стоимость доставки к 1 пункту должна быть ниже 0,49, для 5 оптового торговца стоимость доставки должна быть ниже 0,61
4. Общие издержки при уменьшении потребностей каждого из оптовых торговцев(по отдельности снизятся) снизятся на 1252
5. Общие издержки при увеличении производственных мощностей каждого из пунктов фасовки не получится, так как в таком случае у нас увеличится значение потребности для фиктивного оптового торговца, которое не повлияет на наши издержки.
ЗАДАЧА 4. ТОРГИ
Задание
Вы, занимаясь продажей недвижимости, планируете продать 4 участка земли и получили заявки от 5-ти застройщиков. Учитывая величину требуемой суммы, ни один из застройщиков не претендует на покупку более одного участка. Цены в сотнях тысяч рублей, предложенные застройщиками за продаваемые участки, приведены в таблице.
Вы хотите составить оптимальный план продажи участков.
Рекомендации
Сформулируйте модель как задачу о назначениях.
Составьте свою задачу по образцу данной. Измените при этом названия и количество предметов, предлагаемых на продажу, количество поступивших заявок, числа в постановке задачи и, возможно, денежные единицы. При этом количество предлагаемых на продажу предметов должно быть меньше поступивших заявок.
Таблица 5 – Застройщики и участки
| Участок | Застройщики | ||||
| A | 7,200 | 19,000 | 29,000 | 6,147 | 24,000 |
| B | 23,000 | 7,957 | 7,216 | 19,000 | 12,924 |
| C | 19,000 | 5,078 | 8,336 | 0,000 | 20,000 |
| D | 6,147 | 0,000 | 19,000 | 7,957 | 6,821 |
Сначала сформулируйте модель линейного программирования в буквенном виде (запишите на бумаге), затем решите ее с помощью программы. В Excel представьте модель в 2-х вариантах, с числами и формулами, а также получите отчет об устойчивости.
Оптимальное решение

Рисунок 14 - Решение

Рисунок 15 - Используемые формулы
Отчет о результатах

Рисунок 16 – Отчет о результатах

Рисунок 17 – Отчет о результатах (продолжение)
4.4 Ответы на вопросы задания
1. На участок А будет назначен поставщик 2, на участок В будет назначен поставщик 1, на участок С будет назначен поставщик 5, на участок D будет назначен поставщик 3, на участок E(фиктивный участок) поставщик 4, т.е он окажется не назначенным ни на один из участков.
2. Участок А будет продан по цене 19, участок В будет продан по цене 23, участок С будет продан по цене 20, участок D будет продан по цене 19.
3. Максимальная выручка, полученная от продажи равна 81.
СПИСОК ЛИТЕРАТУРЫ
А.Л. Кутузов
Исследование операций. Линейная оптимизация в Excel и WinQSB. — СПб.: Изд-во Политехн. ун-та, 2015.