В 1879 г. Стефан экспериментально ( ~ Т 4), а в 1884 г. Больцман теоретически на основе законов термодинамики нашли выражение для
~ Т 4), а в 1884 г. Больцман теоретически на основе законов термодинамики нашли выражение для  - излучательности абсолютно черного тела.
- излучательности абсолютно черного тела.
 Закон Стефана-Больцмана: Излучательность абсолютно черного тела пропорциональна четвертой степени абсолютной температуры.
Закон Стефана-Больцмана: Излучательность абсолютно черного тела пропорциональна четвертой степени абсолютной температуры.
 = s Т 4 (11)
= s Т 4 (11)
s = 5,67 . 10-8 Вт/м2К4 – постоянная Стефана-Больцмана.
Вид зависимости спектральной плотности излучательности а.ч.т. от его температуры и длины волны был изучен экспериментально на модели а.ч.т. в конце ХIХв.:
 |
Рис. 5
Анализ экспериментальных зависимостей  :
:
1. С повышением температуры площадь под кривыми, определяющая излучательность абсолютно черного тела  , резко возрастает, что соответствует закону Стефана-Больцмана.
, резко возрастает, что соответствует закону Стефана-Больцмана.

2. Спектр абсолютно черного тела сплошной, т.е. в нем представлен непрерывный ряд l.
3. Энергия в спектре абсолютно черного тела распределяется неравномерно.
4. С повышением температуры неравномерность распределения энергии по длинам волн усиливается.
5. Max спектральной плотности излучательности с повышением температуры смещается в сторону коротких длин волн, т.е. если Т 3 > Т 2 > Т 1,
то lmax 1 > lmax 2 > lmax 3.
Немецкий физик В.Вин, опираясь на законы термо- и электродинамики, установил зависимость длины волны λmax, соответствующей максимальному значению спектральной плотности излучательности r*λ,Т, от температуры Т.
 Длина волны lmax на которую приходится max спектральной плотности излучательности абсолютно черного тела обратно пропорционально абсолютной температуре.
Длина волны lmax на которую приходится max спектральной плотности излучательности абсолютно черного тела обратно пропорционально абсолютной температуре.
 - первый закон Вина, закон смещения (12)
- первый закон Вина, закон смещения (12)
b = 2,9 . 10-3 м К – постоянная Вина.
5. Максимальная спектральная плотность излучательности абсолютно черного тела пропорциональна пятой степени абсолютной температуры.
 |

С = 1,3 . 105 Вт/м3К5 – вторая постоянная Вина.
ЗАКОН ИЗЛУЧЕНИЯ ПЛАНКА
Закон излучения Планка – это закон распределения энергии в спектре абсолютно черного тела при определенной температуре
Законы Стефана-Больцмана и Вина на дают общей картины распределения энергии по длинам волн при различных температурах. В связи с этим в конце прошлого столетия был предпринят ряд попыток теоретически установить закон распределения энергии в спектре излучения абсолютно черного тела, т.е. получить формулу, отражающую зависимость спектральной плотности излучательности абсолютно черного тела  от длины волны и абсолютной температуры
от длины волны и абсолютной температуры  . Иначе необходимо было найти выражения для универсальной функции Кирхгофа.
. Иначе необходимо было найти выражения для универсальной функции Кирхгофа.
Д. Релей и Д. Джине сделали попытку определить f (l, Т), исходя из теоремы классической статистики о равном распределении энергии по степеням свободы.
При этом тепловое излучение принималось равновесным и рассматривалось как совокупность пространственных стоячих электромагнитных волн. Ими было полу  чено выражение
чено выражение
 ,
,
получившее название формулы Релея-Джинса. Оно удовлетворительно согласуется с экспериментальными данными лишь при больших длинах волн и резко с ними расходится в области коротких длин волн.
Формула Релея-Джинса противоречит закону смещения Вина и закону Стефана-Больцмана. Согласно полученного ими выражения  монотонно возрастает с уменьшением длины волны, не имея максимума, и излучательность абсолютно черного тела
монотонно возрастает с уменьшением длины волны, не имея максимума, и излучательность абсолютно черного тела  обращается в бесконечность при любой конечной (Т ¹ 0) абсолютной температуре (по закону Стефана-Больцмана
обращается в бесконечность при любой конечной (Т ¹ 0) абсолютной температуре (по закону Стефана-Больцмана  - конечная величина). Этот результат получил в физике название «ультрафиолетовой катастрофы»
- конечная величина). Этот результат получил в физике название «ультрафиолетовой катастрофы»
( ® ¥ при l ® 0).
® ¥ при l ® 0).
Таким образом, в рамках классической физики не удалась объяснить законы распределение энергии в спектре абсолютно черного тела.
В 1900 г. М. Планк (нем. 1858 – 1947 гг.) высказал гипотезу, из которой следовало, что абсолютно черное тело излучает энергию не непрерывно, а определенными дискретными порциями – квантами. Он представлял излучающее тело как совокупность огромного количества осцилляторов, энергия которых может изменяться лишь на величину, кратную hn.

h = 6,62 . 10-34 Дж.с – постоянная Планка (квант действия;
действие = работа ´ время).
Постоянная Планка h является одной из универсальных в физике.
Если излучение испускается порциями hn, то излученная энергия должна быть кратной величине этой порции, т.е.
Wизл = N hn (N = 1, 2, 3,...)
На основании представлений о квантовом характере теплового излучения М. Планк, пользуясь статическим методом, получил следующие выражения для спектральной плотности излучения (универсальной функции Кирхгофа):

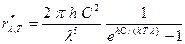
и
 .
.
День 14.12.1900 г., когда Планк доложил в немецком физическом обществе о теоретическом выводе закона излучения, стал датой рождения квантовой теории (нобелевская премия, 1918 г.).
Зависимость  от длины волны (частоты) выраженная формулой Планка, находится в полном соответствии с экспериментальной для всех длин волн и температур.
от длины волны (частоты) выраженная формулой Планка, находится в полном соответствии с экспериментальной для всех длин волн и температур.
Пользуясь формулой Планка, легко получить законы Стефана-Больцмана и Вина.
Если проинтегрировать  по всем длинам волн, то получим закон Стефана-Больцмана
по всем длинам волн, то получим закон Стефана-Больцмана
 ,
,
где  Вт/м2К4.
Вт/м2К4.
Если исследовать функцию планка на экстремум, то получим закон Вина и выражение для постоянной Вина:
 , откуда lmax Т = b,
, откуда lmax Т = b,
b =  м К.
м К.
Таким образом формула М. Планка дает исчерпывающие описание равновесного теплового излучения.
К практическому занятию:
Поток излучения:
 (Вт).
(Вт).
Поглощаемый поток
 (Вт)
(Вт)
Коэффициент излучательности (степень черноты)
 . Для абсолютно черного тела
. Для абсолютно черного тела 
Для «нечёрных» тел  .
.
 .
.
Солнечная постоянная

Земля
rзо
S
Солнце
Рис.6.