При конструировании одежды рациональная конструкция деталей может быть разработана на основе использования геометрических свойств тканей: изменять угол между нитями основы и утка, что позволяет очень просто создавать объемную форму.
Чебышев П. Л. – великий русский математик академик, в 1878 году доказал возможность аналитического расчета разверток плотно облегающих оболочек из ткани для различных поверхностей в своей работе «О кройке одежды».
Основной задачей расчета разверток деталей одежды является определение их рациональной формы, обеспечивающей одевание данной поверхности плоским материалом наиболее простым способом при минимальной площади разверток и наименьшем количестве швов.
Применение чебышевской сети для построения разверток (деталей одежды) оболочек.
П.Л.Чебышев четко сформулировал условия, определяющие характер изменений, происходящих с тканью, когда она становится оболочкой какого-либо тела, и выбрал удобную координацию поверхности. При этом он исходил из следующих положений:
1) нити основы и утка ткани в ее первоначальной плоской форме пересекаются между собой под прямыми углами, образуя прямоугольную сеть;
2) при покрывании тканью криволинейной поверхности ее нити изгибаются, а небольшие прямоугольники, образуемые нитями, превращаются в параллелограммы. При этом допускается, что при покрывании поверхности в ткани изменяются только углы наклона нитей основы и утка, длина же нитей остается неизменной;
3) при превращении прямоугольников в параллелограммы ткань оказывает заметное сопротивление растяжению только в случае, когда растягивающие силы направлены по длине нитей основы и утка;
4) натянутые нити будут находиться в равновесии лишь при условии, если они расположатся по кратчайшим (геодезическим) линиям поверхности.
Полагая, что эти нити пересекаются между собой под прямым углом, П.Л.Чебышев принимает их за исходные ортогональные геодезические оси координат (ОХ, ОY) за координаты длину нитей основы и утка. Когда ткань имеет первоначально плоскую форму, эти координаты прямолинейны и прямоугольны. При облегании тканью поверхности координаты становятся криволинейными, значения их остаются неизменными.
П.Л.Чебышев рассматривает нити ткани как координатные линии, образующие на плоскости прямолинейную прямоугольную, а на поверхности – криволинейную (чебышевскую) нить. Элементами сети на плоскости являются бесконечно малые прямоугольники, а на поверхности – параллелограммы с одной и той же длиной сторон dx и dy.
Расстояние между соседними точками ткани на плоскости определяется длиной диагонали элементарного прямоугольника 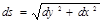 на поверхности – диагонали элементарного параллелограмма:
на поверхности – диагонали элементарного параллелограмма:
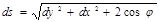 dydx
dydx 
где φ - угол наклона нитей основы и утка (сетевой угол) в точке (X, Y).
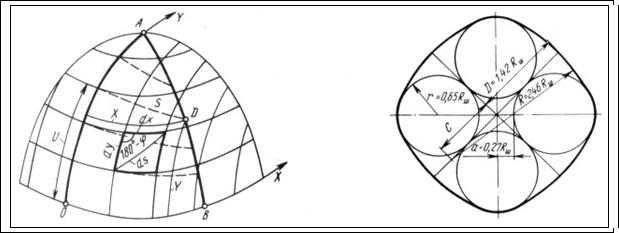
| Рис.3. | Схема оболочки из ткани на поверхности сферы и ее координация для расчета разверток оболочек по П.Л.Чебышеву | Рис.4. | Графический способ построения развертки – оболочки для шара из двух частей. |
Исходя из этого уравнения, П.Л.Чебышев решил поставленную задачу об одевании поверхности тканью в виде следующих формул [20]:
X = S +  (K0²U² + K0 K2 U³+
(K0²U² + K0 K2 U³+ 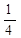 K2 U4)S³ +
K2 U4)S³ + 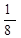 (K0 K1 U²+
(K0 K1 U²+ 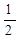 K1 K2 U³)S4 +....;
K1 K2 U³)S4 +....;
Y = U – (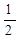 K0 U +
K0 U + 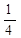 K2 U²)S²+
K2 U²)S²+ 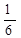 K1 US³ +...,
K1 US³ +...,
где X и Y – прямоугольные координаты точек, определяющих форму развертки оболочки из ткани; S – кратчайшее расстояние от оси OY до точек (X,Y), заданных на линии шва оболочки на поверхности тела; U – ордината на поверхности тела точки пересечения линии кратчайшего расстояния (S) оси OY; K0, K1, K2 - коэффициенты разложения в степенной ряд гауссовой кривизны в данной точке поверхности (X,Y).(Рис.4).
Координаты S и U в формулах П.Л.Чебышева – ортогональные геодезические линии. Их можно измерять непосредственно с помощью геодезического угольника (см.рис. 1в).
3. Условия применения чебышевской сети для построения разверток оболочек свободного облегания. В основе теории расчёта развёрток деталей одежды лежит решение геометрической задачи одевания поверхности тканью. Вследствие того что ткань является сетчатым материалом, она образует на поверхности криволинейную сеть, в которой противоположные стороны каждого четырёхугольника равны между собой. В одежде, изготовленной из клетчатой ткани с некрупной клеткой, легко заметить, что прямоугольные клетки изменяются на кривых участках поверхности тела в параллелограммы.
Два семейства линий, пересекающихся на поверхности, в дифференциальной геометрии называют сетью. Сеть, образующую на поверхности четырёхугольники с равными противоположными сторонами, называют сетью Чебышева, или чебышевской сетью. Основные свойства чебышевской сети состоят в том, что пересекающиеся линии сети вполне определяют положение на поверхности всех остальных её линий, так как линии каждого семейства в отдельности располагаются параллельно друг другу. Поэтому чебушевскую сеть можно построить на любой поверхности путём параллельного переноса линий сети (рис. 2.54, а).
Однако решение поставленной П. Л. Чебышевым задачи об определении формы разверток оболочек из тканей для различных тел, несмотря на то, что ее решением занимались многие отечественные и зарубежные математики, долгое время не было доведено до практического применения. Это объясняется сложностью геометрической задачи, поставленной П. Л. Чебышевым, и отсутствием простых инженерных методов ее решения.
Наиболее полное развитие задача П. Л. Чебышева получила в работах А. В. Савостицкого. Им были определены условия применения чебышевской сети для построения разверток не только плотно облегающих оболочек из ткани, но и оболочек свободного облегания, к числу которых относится одежда.
Рассмотрим эти условия.
Первое условие. Необходимо производить закрепление деталей одежды, полученной в результате изменения углов наклона (перекоса) нитей в оболочке посредством влажно-тепловой обработки (горячее прессование или пропаривание и сушка).
Второе условие. Применяя чебышевскую сеть для определения формы разверток оболочек из ткани, необходимо учитывать, что максимальное изменение углов между нитями основы и утка (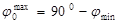 ) можно производить в пределах допускаемого для данной ткани угла перекоса нитей
) можно производить в пределах допускаемого для данной ткани угла перекоса нитей 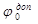 , т. е.
, т. е. 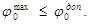
Рис. 5- Схема определения допускаемого угла перекоса нитей основы и утка в ткани
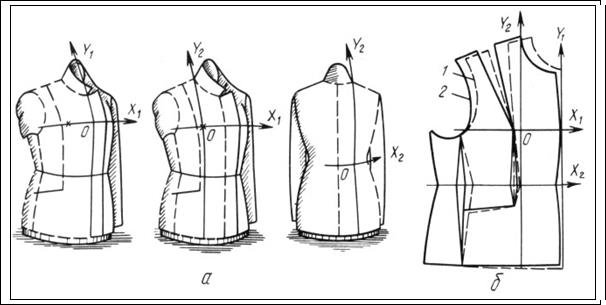
Рис. 6. Положение исходных осей координат на поверхности изделия (а) и форма развертки полочки при различном положении осей координат (б)
Третье условие. Обязательное задание объемной формы поверхности одежды образцом модели, надетым на манекен внутренней формы или манекен внешней формы изделия. Конструирование разверток деталей так называемых плоских оболочек (воротников, нижних участков рукавов, подбортов, брюк) осуществляется с применением плоских шаблонов.
Установлено, что на изменение угла между нитями ткани влияет положение исходных осей координат (рис.6). Чем меньше угол перекоса, тем более рациональной является развертка, так как площадь элементарных параллелограммов на поверхности будет незначительно отличаться от площади элементарных прямоугольников на плоскости.