ЗАДАНИЯ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ
Задания следует оформлять в отдельной тетради, на обложке которой кроме фамилии и номера группы должны быть указаны следующие данные:
a =, b =, g =, q =, m =, n =.
Здесь a - номер факультета (института) b– год поступления, g и q– две последние цифры номера группы, m и n– две цифры номера студента по списку.
Так, у пятого студента группы 710062 a = 7, b = 0, g = 6, q = 2, m = 0, n = 5 .
Задание 1
Прибор, установленный на борту самолета, может работать в двух режимах: в условиях нормального крейсерского полета и в условиях перегрузки при взлете и посадке. Крейсерский режим полета осуществляется в (70+10m+ν)% всего времени полета. Вероятность выхода прибора из строя за время полета в нормальном режиме равна 0,1(m+1), в условиях перегрузки 0,1a+0,01ν. Вычислить надежность прибора за время полета.
Задание 2
Прибор состоит из двух последовательно включенных узлов. Надежность (вероятность безотказной работы в течение времени Т) первого узла равна 0,1a+0,01(10m+ν), второго 0,01+0,1g. За время испытания прибора в течение времени Т зарегистрирован отказ прибора. Найти вероятности следующих событий:
1) А1={отказал только первый узел}
2) A2={отказали оба узла}
Задание 3
Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого из элементов в одном опыте равна p =(10μ+ν+θ)%. Случайная величина Х – число отказавших элементов в одном опыте. Определить следующие характеристики СВ Х:
1) закон распределения СВ Х;
2) построить многоугольник распределения СВ Х;
3) F(x) и построить ее график;
4) M(X);
5) D(X) и σ(X);
6)  ;
;
7) β(X) – коэффициент асимметрии;
8) γ(X) – коэффициент эксцесса;
9) моду СВ Х.
Определить вероятность того, что в одном опыте откажут
|
|
а) не более двух элементов
б) хотя бы один элемент.
Задание (кроме пунктов 2,3 и 9) выполнить с использованием статистических функций EXCEL. Пункты а) и б) выполнить на Scilab.
Пояснение.
Вероятность получить не больше х успехов по формуле Бернулли
Вычисляется с помощью функции cdfbin, которая может записываться так:
[P,Q]=cdfbin("PQ",S,Xn,Pr,Ompr)
[S]=cdfbin("S",Xn,Pr,Ompr,P,Q)
[Xn]=cdfbin("Xn",Pr,Ompr,P,Q,S)
[Pr,Ompr]=cdfbin("PrOmpr",P,Q,S,Xn)
Здесь S - число успехов в Xn опытах, Pr – вероятность успеха в одном опыте, Ompr=1- Pr, Q=1 – P.
Найдем вероятность того, что произойдет отказ не более двух элементов из трех имеющихся, если вероятность отказа одного элемента равна 0,6.
а) Не более двух элементов – это либо 0, либо 1, либо 2 элемента.
P3(x£2)=P3(0)+P3(1)+P3(2)=1-P3(3)
cdfbin("PQ",2,3,.6,.4)
ans =
0.784
Вероятность того, что откажут ровно два элемента можно вычислить так:
cdfbin("PQ",2,3,.6,.4)-cdfbin("PQ",1,3,.6,.4)
ans =
0.432
Задание 4
В результате анализа качества изготовляемых предприятием изделий установлено, что в среднем брак составляет (m+n)%. За смену предприятие выпускает m =100+m+g изделий.
1. вычислить М(Х) и D(Х) (Х – число бракованных изделий за смену)
2. Рm(q+n+5)
3. Pm (не более m+n бракованных изделий)
4. Рm(0)
Пункты 2,3,4 выполнить на EXCEL и Scilab.
Пояснение.
Вероятность получить не больше х успехов по формуле Пуассона
[P,Q]=cdfpoi("PQ",S,Xlam)
[S]=cdfpoi("S",Xlam,P,Q)
[Xlam]=cdfpoi("Xlam",P,Q,S);
S – число успехов в формуле Пуассона;
Xlam - 
P – вероятность того, что интересующее нас событие произойдет не менее S раз;
Q=1-Р
|
|
Найдем вероятность того что в 100 независимых испытаниях, в каждом из которых некоторое событие А может произойти с вероятностью 0.7, событие А произойдет не более 7 раз.

p=cdfpoi("PQ",7,7)
p =
0.5987138
Вероятность того, что интересующее нас событие наступит ровно 12 раз:

p=cdfpoi("PQ",12,7)-cdfpoi("PQ",11,7)
p =
0.0263498
Задание 5
Плотность распределения f(x) вычисляется по формуле:

Найти
1) Константу c
2) F(x) и построить ее график
3)  и
и 
4) М(Х) и D(X)
Задание 6
Случайная величина X распределена нормально с параметрами:  и
и  . Что больше,
. Что больше,  или
или  ?
?
Задачу решить с использованием статистических функций EXCEL и Scilab.
Пример вычислений в Scilab.
cdfnor – функция распределения нормально распределенной СВ с параметрами  (Std) и m (Mean). Q=1-P, X – верхний предел интегрирования.
(Std) и m (Mean). Q=1-P, X – верхний предел интегрирования.

Может записываться так:
[P,Q]=cdfnor("PQ",X,Mean,Std)
[X]=cdfnor("X",Mean,Std,P,Q)
[Mean]=cdfnor("Mean",Std,P,Q,X)
[Std]=cdfnor("Std",P,Q,X,Mean)
СВХ распределена по нормальному закону с 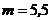 и
и  . Вычислить
. Вычислить 
cdfnor("PQ",3.9,5.5,1.08) -cdfnor("PQ",2.9,5.5,1.08)
ans =
0.0612060
Задание 7
Производится взвешивание некоторого вещества без систематических погрешностей. Случайные погрешности взвешивания подчинены нормальному закону распределения с  г. Найти вероятность того, что взвешивание будет произведено с погрешностью, не превышающей по модулю
г. Найти вероятность того, что взвешивание будет произведено с погрешностью, не превышающей по модулю  г. Задачу решить с использованием статистических функций EXCEL и Scilab.
г. Задачу решить с использованием статистических функций EXCEL и Scilab.
Указание: необходимо вычислить  .
.  ,
,  .
.
Задание 8
Закон совместного распределения случайного вектора (X,Y) задан таблицей
| Y X | 
| 
| 
|

| 0,2 | 
| 0,4 |

| 
| 0,04 | 0,06 |
Вычислить  вручную и в Scilab
вручную и в Scilab
|
|
Пример
Коэффициент корреляции для таблицы
| XY | |||
| 0,1 | 0,2 | 0,2 | |
| 0,3 | 0,1 | 0,1 |
вычисляется в Scilab так:
cls
x=[0 1 2];
y=[2 4];
fre=[0.1 0.2 0.2; 0.3 0.1 0.1]';
r=correl(x,y,fre)
r =
- 0.3611576