Список вопросов по Линейной Алгебре
1. Матрицы. Основные операции над матрицами.
Матрица – это производная таблица чисел.
Две матрицы А и В одного и того же размера m*n называются равными, если они совпадают поэлементно, т.е.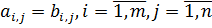 
.
Основные операции над матрицами.
· Умножение матрицы на число. Произведение матрицы А на число ƛ называется матрица В (В=ƛ*А), элементы которой вычисляются как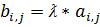 
, 
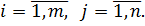
· Суммой двух матриц А и В одинакового размера m*n называется матрица С=А+В, элементы которой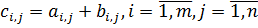 
.
· Разность двух матриц одинакового размера определяется через предыдущие операции, т.е. А-В=А+(-В)
· Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц называется такая матрица С, каждый элемент которой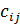 
равен сумме произведений элементов i-строки матрицы А на j-столбец матрицы В.
2. Квадратная матрица. Диагональная и единичная матрицы. Примеры
Классификация матриц.
1) Матрица, состоящая из одной строки/столбца, называется вектор-строка/вектор-столбец.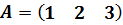 
; 
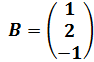
2) Кв. матрицей n-го порядка наз-ся матрица, у которой число строк равняется числу столбцов.
3) Элементы матрицы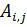 
, у которой i=j, называется диагональными. Они образуют главную диагональ.
4) Если все недиагональные эл-ты матрицы равны нулю, то она называется диагональной.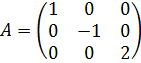 
5) Единичной называется диагональная матрица, элементы которой равны 1.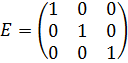 
6) Симметричной называется квадратная матрица, у которой элементы, расположенные симметрично относительно главной диагонали, равны.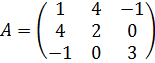 
7) Треугольная матрица – это кв. матрица, у которой все эл-ты, стоящие по одну из сторон главной диагонали равны 0.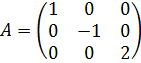
3. Транспонированная матрица. Пример.
Транспонирование матрицы – это переход от матрицы A к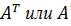 
, в которой строки и столбцы поменялись местами с сохранением порядка.
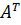называется транспонированной относительно матрицы А.
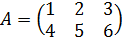
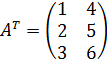
4. Элементарные строчечные преобразования. Эквивалентные матрицы.
· перестановка местами любых двух строк матрицы;
· умножение любой строки матрицы на константу k, k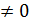 
· прибавление к любой строке матрицы другой строки.
Аналогично определяются элементарные преобразования столбцов.
Элементарные преобразования обратимы.
Если от матрицы A к матрице B перешли с помощью эквивалентных преобразований над строками, то такие матрицы называются эквивалентными и обозначают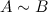 
.
5. Выражение определителя непосредственно через его элементы (для кв. матриц размера 2*2 и 3*3)
Каждой квадратной матрице А можно поставить в соответствие вычисленное по определенным правилам число, называемое определителем кв. матрицы.
Определителем матрицы второго порядка или определителем второго порядка называется число, которое вычисляется по формуле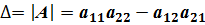 
Определителем матрицы третьего порядка или определителем третьего порядка называется число, которое вычисляется по формуле: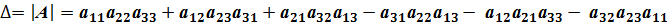 
6. Минор квадратной матрицы, соответствующие элементу матрицы.
Пусть матрица А является кв. матрицей n-ого порядка. Минором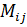 
элемента 
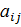называется определитель (n -1)ого порядка, полученный из матрицы А вычеркиванием i – ой строки и j –ого столбца.
Пример: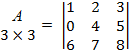 
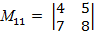
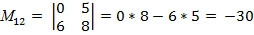
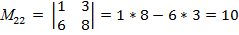
7. Алгебраическое дополнение квадратной матрицы, соответствующие элементу матрицы
АЛГЕБРАИЧЕСКОЕ ДОПОЛНЕНИЕ — понятие матричной алгебры; применительно к элементу aij квадратной матрицы А образуется путем умножения минора элемента aij на (–1)i+j (обозначается Аij):
Aij = (–1)i+j Mij, где Mij — минор элемента aij матрицы A=[aij], т. е. определитель матрицы, полученной из матрицы A вычеркиванием строки и столбца, на пересечении которых стоит элемент aij. Понятие А. д. используется, в частности, в операции обращения матрицы.
8. Вычисление определителя путем разложения по любой строке (столбцу) матрицы
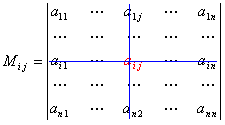
Выберем i,j-ый элемент этой матрицы и вычеркнем i-ую строку и j-ый столбец. В результате мы получаем матрицу (n – 1)-го порядка, определитель которой называется минором элемента и обозначается символом Mi j:
Алгебраическое дополнение Ai,j элемента ai j определяется формулой
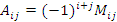
Теорема о разложении определителя по элементам строки. Определитель матрицы A равен сумме произведений элементов строки на их алгебраические дополнения:
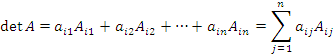
Теорема о разложении определителя по элементам столбца. Определитель матрицы A равен сумме произведений элементов столбца на их алгебраические дополнения:
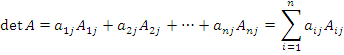
9. Свойства определителей
· При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.
· Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.
· Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.
· Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).
· Общий множитель элементов какой-либо строки определителя можно вынести за знак определителя.
· Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.
· Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.
· Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
· Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей (cм. также формулу Бине-Коши).
10. Невырожденные матрицы. Пример.
Определение. Невырожденной матрицей называется квадратная матрица -го порядка, определитель которой отличен от нуля. В противном случае матрица называется вырожденной.
11. Обратная матрица.
Матрица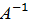 
называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную, как справа таи и слева получается единичная матрица:
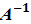* А = А * 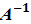= Е
Если определитель матрицы отличен от 0, то такая матрица называется неособенной,в противном случае (при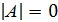 
) такая матрица называется вырожденной или особенной.
Присоединенной матрицей квадратной матрицы А называется матрица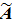 
каждый элемент которой есть алгебраическое дополнение элементов транспонированной матрицы:
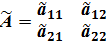
Теорема о существовании обратной матрицы. Обратная матрица А существует и единственна тогда и только тогда, когда исходная матрица невырожденная (неособенная)
12. Формула для вычисления обратной матрицы.
Алгоритм нахождения обратной матрицы
Найти определитель исходной матрицы. Если определитель равен 0, то матрица А – вырожденная и обратной матрицы 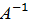не существует.
Если определитель не равен нулю, то находим транспонированную матрицу (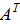
).
Составить присоединенную матрицу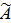 
. Найти алгебраическое дополнение элементов транспонированной матрицы и составить из них присоединенную матрицу.
Вычислить обратную матрицу: =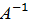 
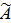* , где 
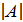- определитель исходной матрицы
Проверить правильность вычислений, исходя из определения: 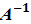* А = А * 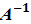= Е
13. Основные свойства обратной матрицы.
· (
= 
* 
· 
· 
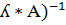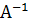
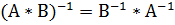
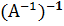=А
· 
= 
=
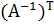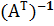14. Ранг матрицы
В матрице размера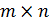 
вычеркиванием каких либо строк и столбцов можно выделить квадратные подматрицы 
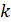- ого порядка, где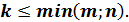 
Определителем таких подматриц называется минорами 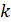– ого порядка матрицы А.
Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы. Обозначается rand A или r (А).
Из определения следует:
· Ранг матрицы размера 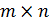не превосходит меньшего из ее размеров, то есть r (А)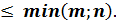 
· r (А) = 0 только тогда, когда все элементы матрицы равны 0, то есть А = 0
· Для квадратной матрицы n – ого порядка r (А)=n, тогда и только тогда, когда матрица А – невырожденная
Определение ранга матрицы перебором всех миноров достаточно трудно. Для облегчения используются элементарные преобразования, сохраняющие ранг матрицы:
· Отбрасывание нулевой строки (столбца).
· Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.
· Изменение порядка строк (столбцов).
· Прибавление к данному элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
· Транспонирование матрицы.
Теор:
· Ранг матрицы не изменится при элементарных преобразованиях матрицы.
· Ранг ступенчатой матрицы равен r, т.к. имеется минор r –ого порядка не равный 0.
15. Теорема Кронекера - Капели
Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.
16. Решение систем линейных уравнений методом Гаусса
Метод гаусса- это метод последовательного исключения переменных; заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого или треугольного вида.
17. Формула Крамера
Метод Крамера (для квадратной матрицы n x n) - Пусть 
- определитель м-цы А, а 1 получен из матрицы с заменой j-го столбца столбцом свободных членов. Тогда, если ≠ 0, то система имеет ед. решение, определенное по формуле Крамера: xj= j / (j=1…n)
18. Фундаментальная система решений (ФСР) однородной системы линейных уравнений.
Называется n − r линейно независимых решений этой системы (или базис ядра оператора)
Теорема о ФСР: пусть ранг основной м-цы, r(A) меньше, чем n (r<n), где n – число переменных, тогда
1) ФСР существует, y1, y2, yk, состоит из k векторов (k=n-r)
2) Общее решение системы имеет вид: Хобщ=c1y1+c2y2+…+cn-ryn-r
3) Если n=r, то ФСР не существует
18. Векторы на плоскости и в пространстве
19. Векторное пространство и его простейшие свойства.
20. Размерность и базис векторного пространства.
Векторное пространство Rn называется n -мерным, если в нем можно найти n линейно независимых векторов, но больше, чем n линейно независимых векторов оно не содержит.
Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов. Rn условимся обозначать через dim.
Пространство, имеющее конечную размерность, называется конечномерным. Пространство, в котором можно найти сколь угодно много линейно независимых векторов, называется бесконечномерным.
Совокупность n линейно независимых векторов n - мерного векторного пространствa Rn называется его базисом.
Теор1. Каждый вектор x линейного n- мерного пространства Rn можно представить, и притом ед. способом, в виде линейной комбинации векторов базиса.
Теор2. Если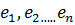 
- линейно независимые векторы пространства Rnи любой вектор 
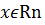линейно выражается через 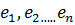, то эти векторы образуют базис в Rn.
Переход к новому базису
Пусть в пространстве Rnимеется два базиса: 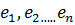и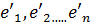 
.
Каждый из векторов нового базиса, можно линейно выразить через векторы старого базиса:
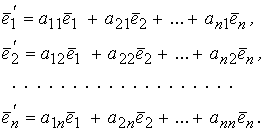
Новые базисные векторы получаются из старых с помощью матрицы
При этом коэффициенты их разложений по старым базисным векторам образуют столбцы этой матрицы. Матрица A называется матрицей перехода от 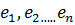базиса к базису 
.
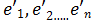22. Скалярное произведение. Евклидово пространство.
Опр.: Скалярным произведением двух векторов (x,y)= ∑ называется число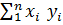 
св-ва: 1) (x,y)=(y,x) 2) (x,y+z)=(x,y)+(x,z) 3) (λx,y)=λ(x,y) λ>0 любое действ.число
4) (x,x)>0(если x≠0)
Опр.: линейное(векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяет свойствам 1-4, называется Евклидовым пространством.
23. Понятие линейного пространства
Линейные операции над векторами обладают след свойствами:
1) x+y=y+x (коммутативный) закон сложения
2) (x+y)+z=x+(y+z) (ассоциативный) закон сложения
3) a(bx)=ab(x), где a,b-действ числа
4) a(x+y)=ax+ay
5) (a+b)x=ax+bx
6) 0=(0,000) нулевой вектор x+0=x
7) для любого X сущетсвует -X
x+(-x)=0
Опр.: множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножение вектора на число, которое удовлетворяет свойствам (1-7), называется векторным(линейным) пространством
24. Линейный оператор. Действия над линейными операторами
Линейный оператор - если задан закон, по которому каждому вектору х пространства Rn ставится в соответствие единственный вектор у пространства Rm, то говорят, что задан оператор А(х), действующий из пространства Rn в Rm
Действия над линейными операторами:
1)(Ã +῀В)*(х)= Ã (х)+῀В(х)
2)(ʎ῀А)(х)=ʎ(Ã (х))
3)(Ã ῀В)(х)=А(В(х))
4)῀0(х)=0
5)῀Е(х)=х
25. Собственные векторы и собственные значения линейного оператора
Опр: Вектор Х≠0-называется собственным вектором матрицы А если найдётся такое число N, что выполняется равенство: AХ=ʎХ(3).
Опр: Число ʎ в равенстве (3) называется собственным значением матрицы А, соответствующий векторуХ. |A- ʎ E|=|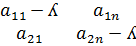 
| - характеристическое уравнение матрицы А
26. Матричная запись линейных операторов.
Связь между вектором х и его образом у= Ã(х) можно выразить в матричной форме У=А*Х, где А – матрица линейного оператора. Вектор Х состоит из координат Х=(х1,х2,…хn), а вектор У из координат У=(х1,х2…хn)
27. Зависимость между матрицами одного и того же оператора в разных базисах (теорема)
Предположим, А и А* - матрицы линейного оператора Ã в базисах А-е1,е2,…еn, А*- е1*,е2*,…еn*, они связаны соотношением А*=С-1*А*С, где С – матрица перехода от старого базиса к новому