Для студентов направлений бакалавриата
Уфа 2012
УДК 378.147:51
ББК 74.58:22.1
М34
Рекомендовано к изданию методической комиссией механического факультета (протокол № 9 от 27 июля 2012 года) и заседанием кафедры математики (протокол № 7 от 10 апреля 2012 года)
Составители: ст. преподаватель, к.т.н. Валиахметова Ю.И.
ст. преподаватель Карамов В.И.
Рецензент: доцент кафедры физики Юмагужин Р.Ю.
Ответственный за выпуск: зав. кафедрой математики
доцент Лукманов Р.Л.
Предварительно приведем вопросы по разделу, на которые следует ответить перед решением задач и на зачете.
1. Основные понятия, связанные с матрицами (матрица-строка, матрица-столбец, определитель квадратной матрицы и т.п.)
2. Сложение матриц и умножение матрицы на число. Свойства этих действий.
3. Умножение матриц и его свойства.
4. Вычисление определителей второго, третьего и высших порядков.
5. Обратная матрица, ее строение.
6. Матричная запись системы линейных алгебраических уравнений, решение ее с помощью обратной матрицы.
7. Решение матричных уравнений с помощью обратной матрицы, по формулам Крамера и методом Гаусса.
8. Исследование системы уравнений первой степени общего вида; основная и расширенная матрицы; ранг матрицы; теорема Кронекера-Капелли.
Далее рассмотрим образец решения некоторых типовых задач.
Задача 1. Вычислить определитель 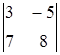
Решение. По формуле 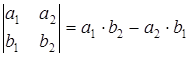 получим:
получим:
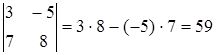
Ответ. 59.
Задача 2. Вычислить определитель 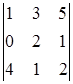
Решение. Используя формулу треугольников
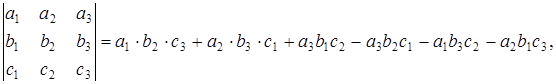 получим:
получим:
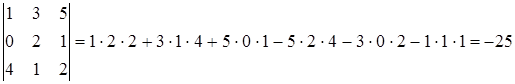
Ответ. -25.
Задача 3. Вычислить определитель 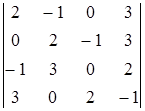 .
.
Решение. Третий столбец определителя содержит два нулевых элемента. Используя теорему Лапласа, разложим определитель по этому столбцу:
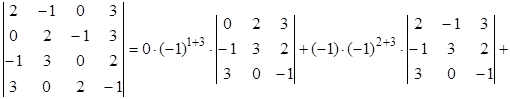
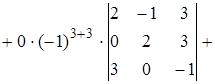
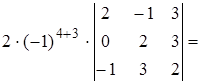
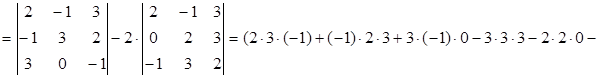
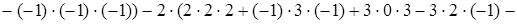
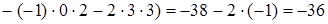 .
.
Ответ. -36.
Задача 4. Вычислить определитель 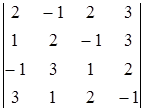 .
.
Решение. Упростим определитель: 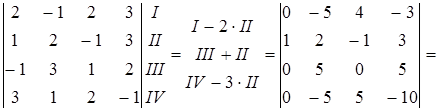
Раскладываем определитель по первому столбцу:
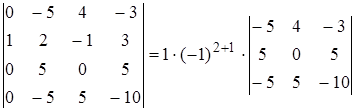
Вынесем общий множитель (5) первого столбца за знак определителя. Получим:
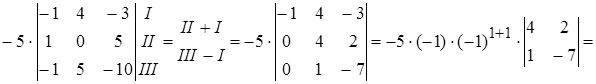
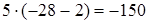
Ответ. -150.
Задача 5. Исследовать систему линейных уравнений; если она совместна, то найти ее общее и одно частное решение.
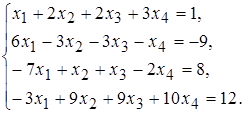
Решение. Приведем расширенную матрицу системы к ступенчатому виду:
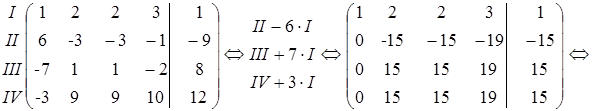
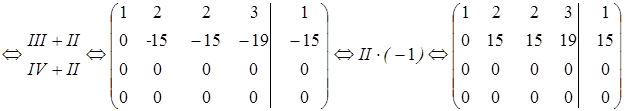
Так как 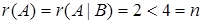 , то система совместна и является неопределенной.
, то система совместна и является неопределенной.
Количество главных переменных равно 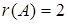 , количество свободных переменных равно
, количество свободных переменных равно 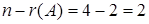 .
.
Выберем какой-нибудь отличный от нуля минор второго порядка полученной матрицы 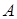 , например, минор
, например, минор 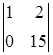 . Его столбцы – первый и второй столбцы матрицы
. Его столбцы – первый и второй столбцы матрицы 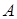 - соответствуют переменным
- соответствуют переменным 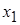 и
и 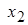 - это будут главные переменные, а
- это будут главные переменные, а 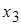 и
и 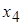 - свободные переменные.
- свободные переменные.
Заметим, что в качестве главных переменных в данном примере нельзя выбрать пару 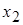 и
и 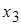 , т.к. любой соответствующий им минор равен нулю:
, т.к. любой соответствующий им минор равен нулю:
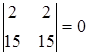 ,
, 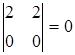 ,
, 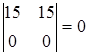 .
.
Запишем систему уравнений, соответствующую полученной расширенной матрице:
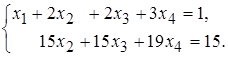
Перепишем ее в виде:
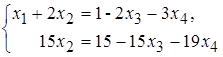 или
или 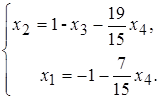
Обозначим свободные переменные: 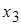 через
через 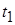 ,
, 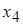 через
через 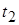 . Запишем общее решение системы:
. Запишем общее решение системы:
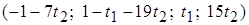 ; частное решение при
; частное решение при 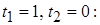
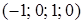 .
.
Ответ. 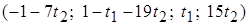 – общее решение,
– общее решение, 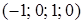 – частное решение системы уравнений.
– частное решение системы уравнений.
Задача 6. Исследовать систему линейных уравнений:
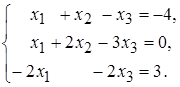
Решение. Приведем к ступенчатому виду расширенную матрицу системы:
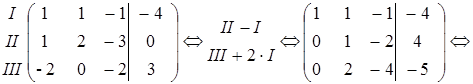
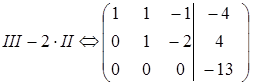
Т ак как 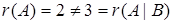 , то система несовместна (не имеет решений). В самом деле, последней строке полученной расширенной матрицы соответствует уравнение
, то система несовместна (не имеет решений). В самом деле, последней строке полученной расширенной матрицы соответствует уравнение 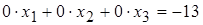 , не имеющее решений.
, не имеющее решений.
Ответ: система несовместна.
Задача 7. Найти общее решение однородной системы линейных уравнений:
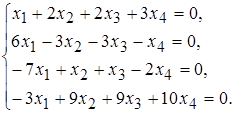
Решение. Приведем матрицу системы к ступенчатому виду:
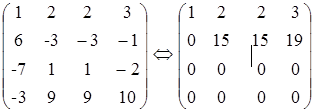
Так как 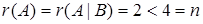 , то система является неопределенной. В качестве главных переменных можно выбрать
, то система является неопределенной. В качестве главных переменных можно выбрать 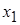 и
и 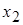 , соответствующие столбцам ненулевого минора второго порядка:
, соответствующие столбцам ненулевого минора второго порядка: 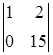 ; в качестве свободных переменных –
; в качестве свободных переменных – 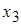 и
и 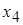 .
.
Запишем систему, соответствующую полученной матрице:
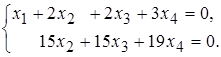
Из второго уравнения получим 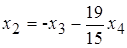 . Подставляя это выражение в первое уравнение, получим
. Подставляя это выражение в первое уравнение, получим 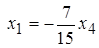 .
.
Обозначая свободные переменные: 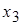 через
через 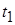 ,
, 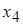 через
через 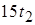 , запишем общее решение системы:
, запишем общее решение системы:
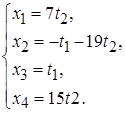 или
или
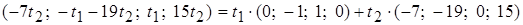 .
.
Ответ. 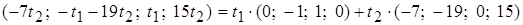 .
.
Задача 8.
Найти матрицу С, если
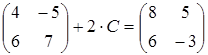
Решение. 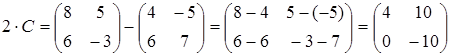 ,
,
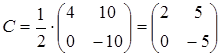 .
.
Ответ. 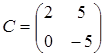
Задача 9. Решить матричное уравнение
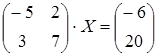
Решение. Если матричное уравнение имеет вид 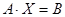 , где
, где 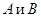 - матрицы, заданные по условию, а
- матрицы, заданные по условию, а 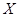 - искомая матрица, то решение уравнения ищется в виде
- искомая матрица, то решение уравнения ищется в виде 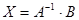 .
.
Найдем обратную матрицу:
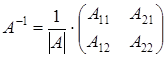 , где
, где 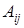 - алгебраические дополнения элементов матрицы
- алгебраические дополнения элементов матрицы 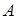 .
.
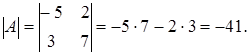
Так как определитель матрицы 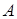 отличен от нуля, то обратная матрица существует и единственна.
отличен от нуля, то обратная матрица существует и единственна.
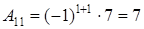 ,
, 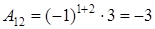 ,
,
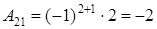 ,
, 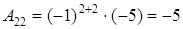 .
.
Тогда
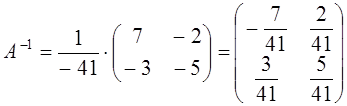 .
.
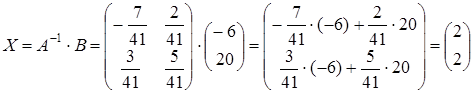 .
.
Проверка. 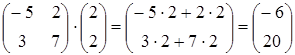 .
.
Ответ. 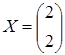 .
.

Задача 10. Решить матричное уравнение
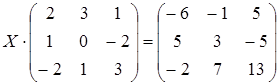
Решение. Если матричное уравнение имеет вид 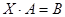 , где
, где 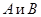 - матрицы, заданные по условию, а
- матрицы, заданные по условию, а 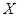 - искомая матрица, то решение уравнения ищется в виде
- искомая матрица, то решение уравнения ищется в виде 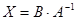 , где
, где 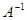 - обратная матрица.
- обратная матрица.
Найдем обратную матрицу: 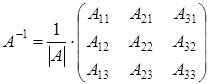 , где
, где 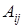 - алгебраические дополнения элементов матрицы
- алгебраические дополнения элементов матрицы 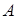 .
.
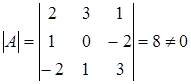 , значит обратная матрица существует и единственна.
, значит обратная матрица существует и единственна.
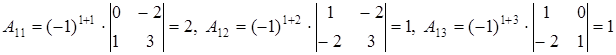
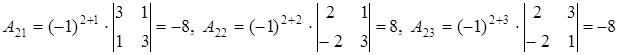
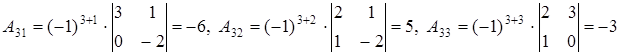
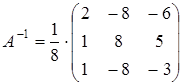 ,
,
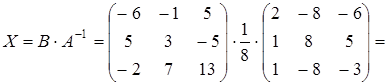
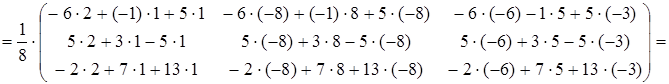
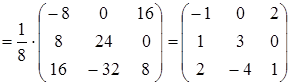 .
.
Проверка.
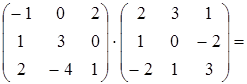
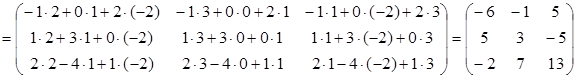
Ответ. 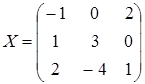 .
.
Задача 11. Решить систему уравнений методом Крамера:
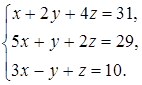
Решение. Найдем определитель матрицы системы:
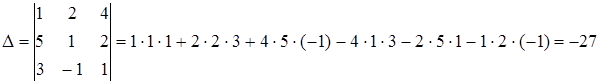 .
.
Так как 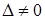 , то система имеет единственное решение.
, то система имеет единственное решение.
Найдем определители 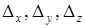 , заменив в матрице коэффициентов соответственно первый, второй, третий столбцы столбцом свободных членов.
, заменив в матрице коэффициентов соответственно первый, второй, третий столбцы столбцом свободных членов.
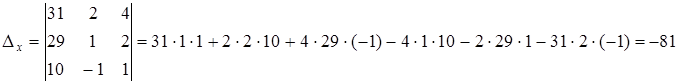
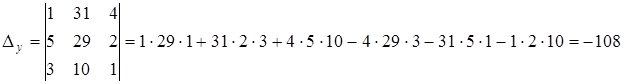
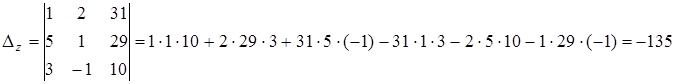
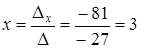 ,
, 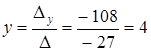 ,
, 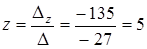 .
.
Ответ. 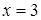 ,
, 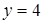 ,
, 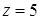 .
.
Задание 1. Вычислить определители матриц:
а) 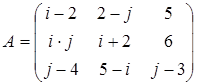 б)
б) 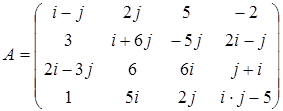
где 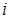 – последняя цифра шифра,
– последняя цифра шифра, 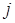 – предпоследняя цифра шифра.
– предпоследняя цифра шифра.
Задание 2. Найдите матрицу 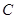 , если:
, если:
1) 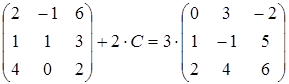 ;
;
2) 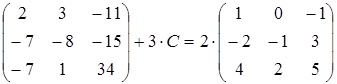 ;
;
3) 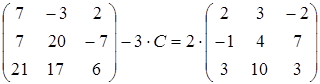 ;
;
4) 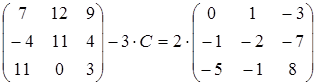 ;
;
5) 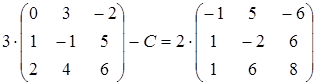 ;
;
6) 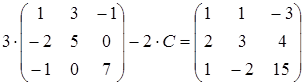 ;
;
7) 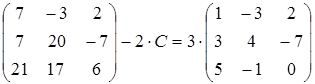 ;
;
8) 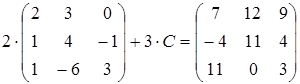 ;
;
9) 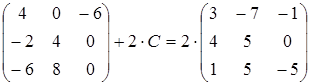 ;
;
10) 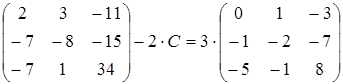 ;
;
11) 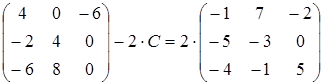 ;
;
12) 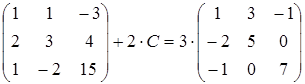 ;
;
13) 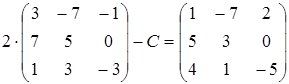 ;
;
14) 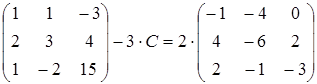 ;
;
15) 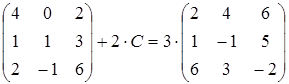 ;
;
16) 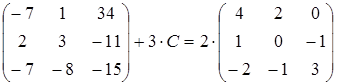 ;
;
17) 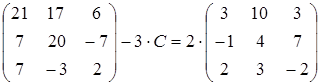 ;
;
18) 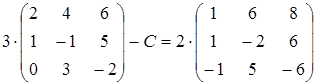 ;
;
19) 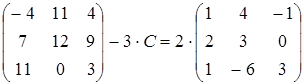 ;
;
20) 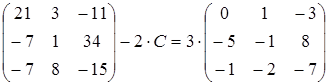 ;
;
21) 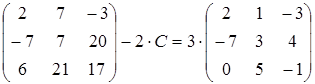 ;
;
22) 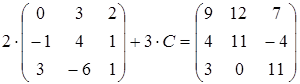 ;
;
23) 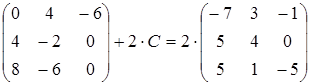 ;
;
24) 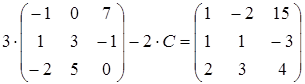 ;
;
25) 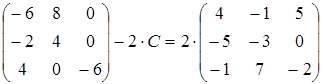 ;
;
26) 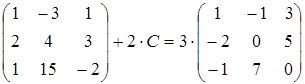 ;
;
27) 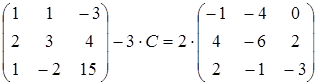 ;
;
28) 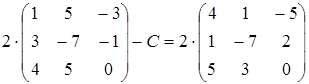 ;
;
29) 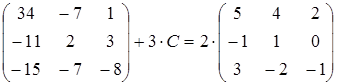 ;
;
30) 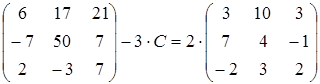 .
.
Задание 3. Решите матричные уравнения и проверьте подстановкой:
1 a) 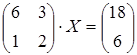 ; б)
; б) 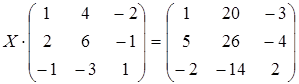 ;
;
2 а) 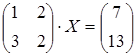 ; б)
; б) 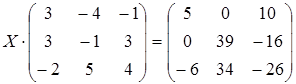 ;
;
3 а) 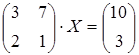 ; б)
; б) 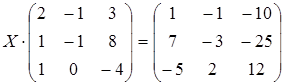 ;
;
4 a) 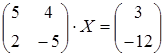 ; б)
; б) 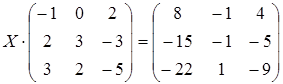 ;
;
5 а) 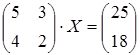 ; б)
; б) 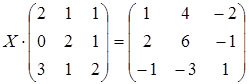 ;
;
6 а) 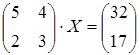 ; б)
; б) 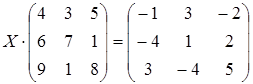 ;
;
7 a) 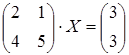 ; б)
; б) 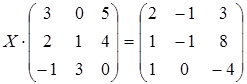 ;
;
8 а) 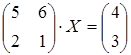 ; б)
; б) 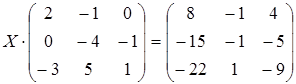 ;
;
9 а) 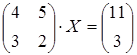 ; б)
; б) 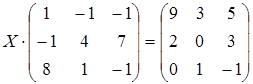 ;
;
10 а) 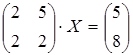 ; б)
; б) 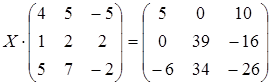 ;
;
11 а) 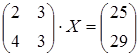 ; б)
; б) 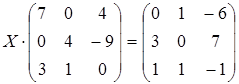 ;
;
12 а) 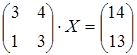 ; б)
; б) 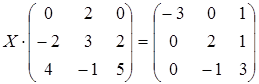 ;
;
13 а) 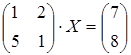 ; б)
; б) 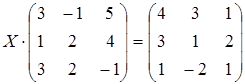 ;
;
14 а) 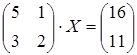 ; б)
; б) 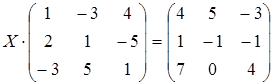 ;
;
15 а) 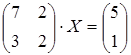 ; б)
; б) 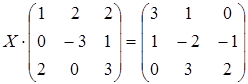 ;
;
16 а) 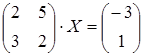 ; б)
; б) 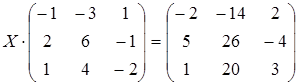 ;
;
17 а) 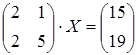 ; б)
; б) 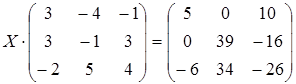 ;
;
18 а) 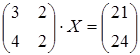 ; б)
; б) 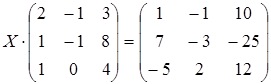 ;
;
19 а) 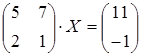 ; б)
; б) 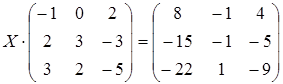 ;
;
20 а) 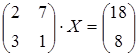 ; б)
; б) 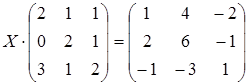 ;
;
21 а) 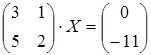 ; б)
; б) 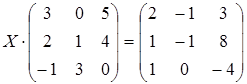 ;
;
22 а) 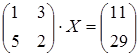 ; б)
; б) 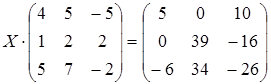 ;
;
23 а) 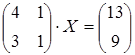 ; б)
; б) 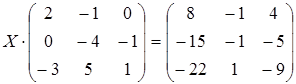 ;
;
24 а) 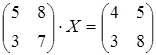 ; б)
; б) 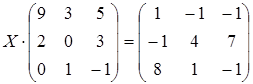 ;
;
25 а) 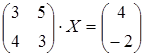 ; б)
; б) 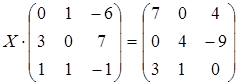 ;
;
26 а) 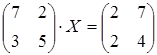 ; б)
; б) 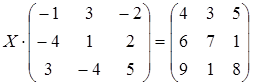 ;
;
27 а) 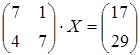 ; б)
; б) 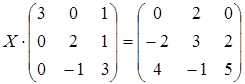 ;
;
28 а) 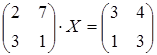 ; б)
; б) 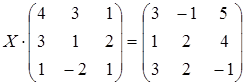 ;
;
29 а) 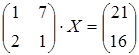 ; б)
; б) 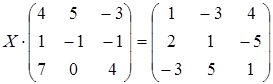 ;
;
30 а) 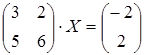 ; б)
; б) 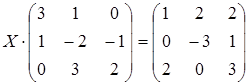 .
.
Задание 4. Решите систему уравнений методом Крамера и с помощью обратной матрицы:
1 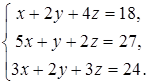 2
2 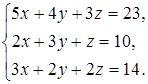
3 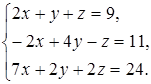 4
4 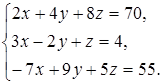
5 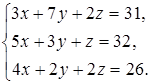 6
6 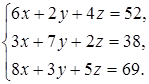
7 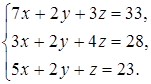 8
8 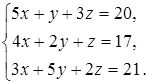
9 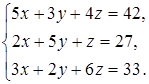 10
10 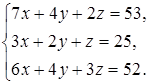
11 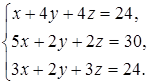 12
12 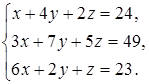
13 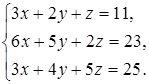 14
14 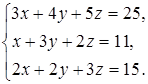
15 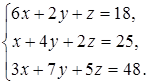 16
16 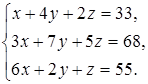
17 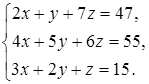 18
18 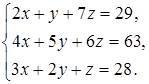
19 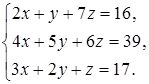 20
20 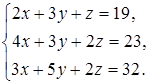
21 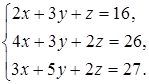 22
22 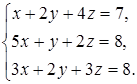
23 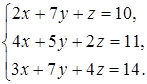 24
24 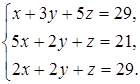
25 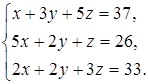 26
26 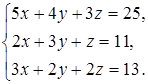
27 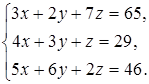 28
28 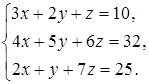
29 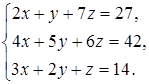 30
30 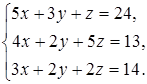
Задание 5. Исследуйте следующие системы уравнений и найдите их решения:
1 а) 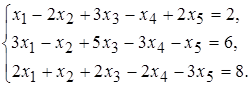 б)
б) 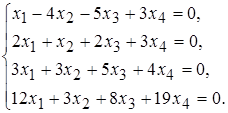
2 а) 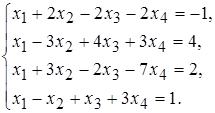 б)
б) 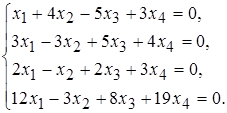
3 а) 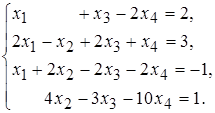 б)
б) 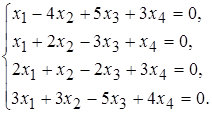
4 а) 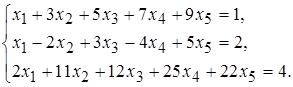 б)
б) 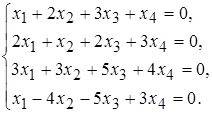
5 а) 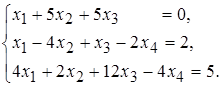 б)
б) 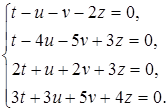
6 а) 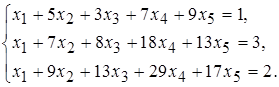 б)
б) 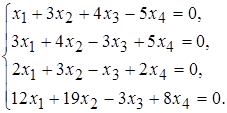
7 а) 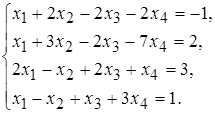 б)
б) 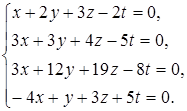
8 а) 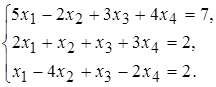 б)
б) 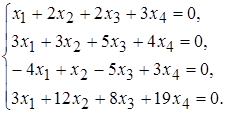
9 а) 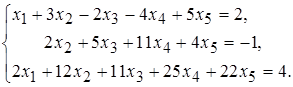 б)
б) 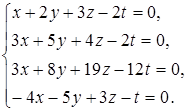
10 а) 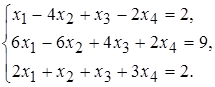 б)
б) 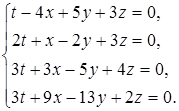
11 а) 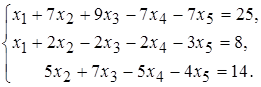 б)
б) 
12 а) 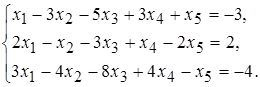 б)
б) 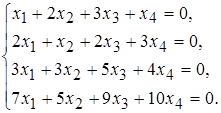
13 а) 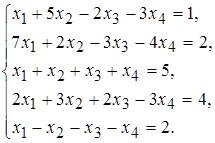 б)
б) 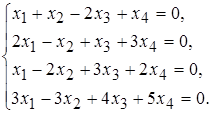
14 а) 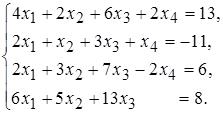 б)
б) 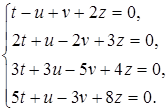
15 а) 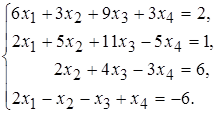 б)
б) 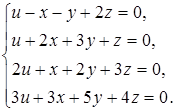
16 а) 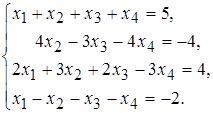 б)
б) 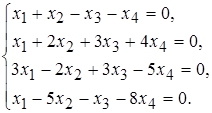
17 а) 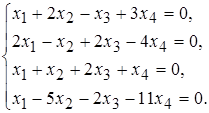 б)
б) 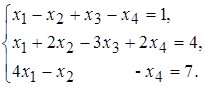
18 а) 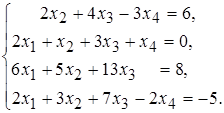 б)
б) 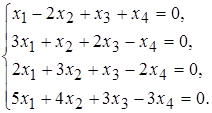
19 а) 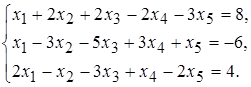 б)
б) 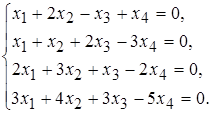
20 а) 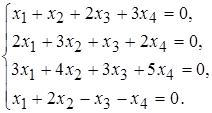 б)
б) 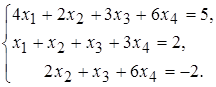
21 а) 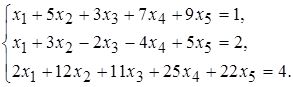 б)
б) 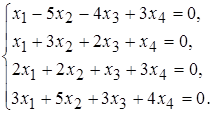
22 а) 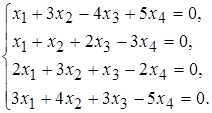 б)
б) 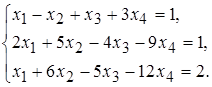
23 а) 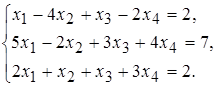 б)
б) 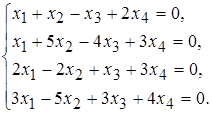
24 а) 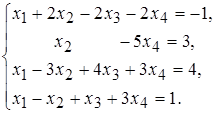 б)
б) 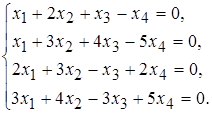
25 а) 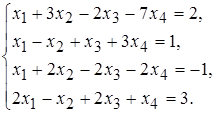 б)
б) 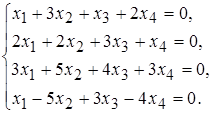
26 а) 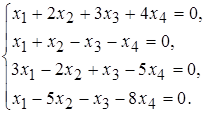 б)
б) 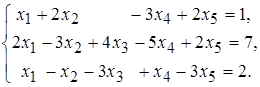
27 а) 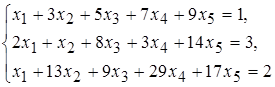 б)
б) 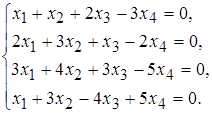
28 а) 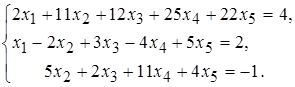 б)
б) 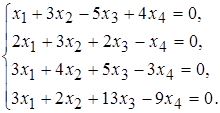
29 а) 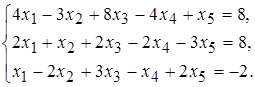 б)
б) 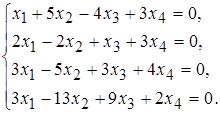
30 а) 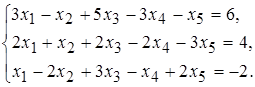 б)
б) 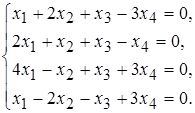
Литература:
1. Письменный Д.Т. Конспект лекций по высшей математике. – М.: Рольф, 2002.-288с., с ил.
2. Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике. 1 курс. – М.: Рольф, 2001.-576с., с ил.