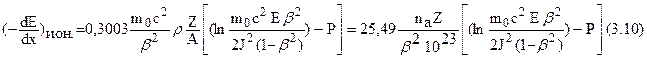
Формулу Бете, по которой оцениваются ионизационные потери заряженных частиц на единицу длины пробега, применительно к электронам с энергией E > 100 эВ можно трансформировать к виду
где (–dE/dx) выражена в кэВ/см; m0c2 = 511 кэВ – энергия массы покоя электрона, b – отношение скорости b-частицы к скорости света, r – плотность среды (г/см3), Z и A – заряд и масса атомов среды, J – средний потенциал возбуждения атомов (кэВ), E-энергия b-частицы (кэВ); na – число атомов в 1 см3 поглощающего материала, P- релятивистская поправка (которой можно пренебречь при E> 10 кэВ).
Потери энергии на излучение, согласно теории Гейтлера, определяются уравнением
Из сопоставления уравнений (3.10) и (3.11) следует, что
1. С увеличением скорости (энергии) ионизационные потери сначала быстро уменьшаются, затем медленно растут (как ln E);
2. Радиационные потери становятся значимыми и быстро растут при E > 1 МэВ – энергии, соответствующей минимуму ионизационных потерь;
3. Ионизационные потери пропорциональны электронной плотности вещества (na·Z); радиационные потери резко увеличиваются с ростом Z (пропорционально na·Z2).
  |
Значения потерь энергии на ионизацию и излучение в материале с высокой электронной плотностью (свинец, Z=82), рассчитанные согласно (3.10) и (3.11), представлены на рис. 3.9.
Соотношение радиационных и ионизационных потерь можно приблизительно оценить [4] по формуле:
(3.12),
где Z – заряд ядра; Eb выражена в МэВ
Удельная ионизация воздуха
По мере продвижения b-частицы в веществе её скорость (энергия) уменьшается, а потери энергии при столкновениях и, следовательно, удельная ионизация среды увеличиваются (см. 3.10). В табл. 3.2 приведено изменение число пар ионов, создаваемых частицей с начальной энергией 5000 кэВ на 1 см пробега в воздухе.
|
|
Таблица 3.2
Линейная ионизация воздуха в зависимости от энергии b-частиц
| Eb, кэВ | 0,140 | ||||
| b = v/c | 0,996 | 0,941 | 0,863 | 0,548 | 0,024 |
| пар ионов на 1 см |
Поглощение энергии и трек b–частиц в воде
Поглощение энергии частиц в облучаемой среде происходит отдельными порциями, величину которых для воды оценивают в 70-100 эВ. В местах поглощения такой порции энергии по следу b-частицы образуется группа из химически активных ионов и радикалов - “шпора”. На образование шпор расходуется примерно половина кинетической энергии b-частиц. В шпоре, средний размер которой ~ 10-20 Å, находится в среднем 2-3 пары ионов и около 6 возбужденных молекул. Расстояние между шпорами примерно 1000 Å.
Гораздо реже шпоры располагаются близко друг к другу и формируют «блоб» – большую шпору. Обычно «блоб» образуют вторичные (выбитые) электроны с энергией 100-500 эВ. Вторичный электрон с энергией более 5000 эВ создает новый трек (d-трек), имеющий собственные шпоры. Схема трека (без учета изменения направления движения b–частицы при столкновениях) представлена на рис. 3.10.
 |
Пробег b-частиц
Истинный пробег b–частиц в веществе определить крайне сложно, т.к. при столкновениях с электронами поглощающего материала они изменяют направление движения. Проникающая способность b–излучения характеризуется величиной максимального пробега Rmax. Rmax. – минимальная толщина поглотителя, который задерживает (поглощает) все b–частицы с начальной энергией Eb,max.
|
|
Истинный пробег b–частиц в веществе примерно в 3-5 раз больше Rmax.
Значения Rmax. в таблицах приводятся, как правило, только для алюминия, однако их можно использовать (с погрешностью до 20%) для оценки проникающей способности b–излучения и в других материалах.
Пример. 32P, Eb,max.= 1,7 МэВ. Табличное значение (для Al) Rmax.= 780 мг/см2. Линейный максимальный пробег Ŕmax. = Rmax./r (r - плотность вещества в мг/см3). Значения Ŕmax.: для алюминия Ŕmax. = 780/2700 = 0,29 см; для воздуха Ŕmax. » 780/1,29 » 605 см.
Для определения Rmax (в г/см2) можно также использовать эмпирические формулы. Например, зависимость типа (для 0,05 МэВ< Eb,max.< 3 МэВ)
(3.13)
Экспериментально установленное значение Rmax. позволяет оценить энергию Eb,max. Например, для 0,003 г/см2 < Rmax. < 1,5 г/см2
(3.14)