CPC
На тему: Интерполяционная формула Гаусса
Выполнил: ст.гр. “ПМиИбк-14”
Туляев Т.T.
Преподаватель кафедры “МИиК”
Назарбаев Ф.Т.
Введение
Иоганн Карл Фридрих Гаусс (30 апреля <https://ru.wikipedia.org/wiki/30_%D0%B0%D0%BF%D1%80%D0%B5%D0%BB%D1%8F> 1777 <https://ru.wikipedia.org/wiki/1777_%D0%B3%D0%BE%D0%B4>, Брауншвейг <https://ru.wikipedia.org/wiki/%D0%91%D1%80%D0%B0%D1%83%D0%BD%D1%88%D0%B2%D0%B5%D0%B9%D0%B3> - 23 февраля <https://ru.wikipedia.org/wiki/23_%D1%84%D0%B5%D0%B2%D1%80%D0%B0%D0%BB%D1%8F> 1855 <https://ru.wikipedia.org/wiki/1855_%D0%B3%D0%BE%D0%B4>, Гёттинген <https://ru.wikipedia.org/wiki/%D0%93%D1%91%D1%82%D1%82%D0%B8%D0%BD%D0%B3%D0%B5%D0%BD>) немецкий <https://ru.wikipedia.org/wiki/%D0%93%D0%B5%D1%80%D0%BC%D0%B0%D0%BD%D0%B8%D1%8F> математик <https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0>, механик <https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%85%D0%B0%D0%BD%D0%B8%D0%BA%D0%B0>, физик <https://ru.wikipedia.org/wiki/%D0%A4%D0%B8%D0%B7%D0%B8%D0%BA>, астроном <https://ru.wikipedia.org/wiki/%D0%90%D1%81%D1%82%D1%80%D0%BE%D0%BD%D0%BE%D0%BC> и геодезист <https://ru.wikipedia.org/wiki/%D0%93%D0%B5%D0%BE%D0%B4%D0%B5%D0%B7%D0%B8%D1%81%D1%82>. Считается одним из величайших математиков всех времён, «королём математиков»[3] <https://ru.wikipedia.org/wiki/%D0%93%D0%B0%D1%83%D1%81%D1%81,_%D0%9A%D0%B0%D1%80%D0%BB_%D0%A4%D1%80%D0%B8%D0%B4%D1%80%D0%B8%D1%85>. Лауреат медали Копли <https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D0%B4%D0%B0%D0%BB%D1%8C_%D0%9A%D0%BE%D0%BF%D0%BB%D0%B8> (1838), иностранный член Шведской <https://ru.wikipedia.org/wiki/%D0%A8%D0%B2%D0%B5%D0%B4%D1%81%D0%BA%D0%B0%D1%8F_%D0%BA%D0%BE%D1%80%D0%BE%D0%BB%D0%B5%D0%B2%D1%81%D0%BA%D0%B0%D1%8F_%D0%B0%D0%BA%D0%B0%D0%B4%D0%B5%D0%BC%D0%B8%D1%8F_%D0%BD%D0%B0%D1%83%D0%BA> (1821) и Российской <https://ru.wikipedia.org/wiki/%D0%A0%D0%BE%D1%81%D1%81%D0%B8%D0%B9%D1%81%D0%BA%D0%B0%D1%8F_%D0%B0%D0%BA%D0%B0%D0%B4%D0%B5%D0%BC%D0%B8%D1%8F_%D0%BD%D0%B0%D1%83%D0%BA> (1824) Академий наук, английского Королевского общества <https://ru.wikipedia.org/wiki/%D0%9B%D0%BE%D0%BD%D0%B4%D0%BE%D0%BD%D1%81%D0%BA%D0%BE%D0%B5_%D0%BA%D0%BE%D1%80%D0%BE%D0%BB%D0%B5%D0%B2%D1%81%D0%BA%D0%BE%D0%B5_%D0%BE%D0%B1%D1%89%D0%B5%D1%81%D1%82%D0%B2%D0%BE>.
Интерполяционные формулы, формулы, дающие приближённое выражение функции  при помощи интерполяции <https://dic.academic.ru/dic.nsf/ruwiki/53634>, то есть через интерполяционный многочлен
при помощи интерполяции <https://dic.academic.ru/dic.nsf/ruwiki/53634>, то есть через интерполяционный многочлен 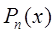 степени
степени  , значения которого в заданных точках
, значения которого в заданных точках  совпадают со значениями
совпадают со значениями  функции
функции 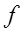 в этих точках. Многочлен
в этих точках. Многочлен 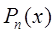 определяется единственным образом, но в зависимости от задачи его удобно записывать различными по виду формулами.
определяется единственным образом, но в зависимости от задачи его удобно записывать различными по виду формулами.
Первая и вторая интерполяционные формулы Гаусса
интерполяционный формула гаусс
Основным недостатком интерполяционных формул Ньютона является то, что они используют лишь односторонние значения функции. На практике часто оказывается полезным использовать формулы, в которых присутствуют как последующие, так и предыдущие значения функции по отношению к ее начальному значению 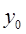 .
.
Рассмотрим 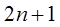 равноотстоящих узлов
равноотстоящих узлов  , в которых заданы значения некоторой функции
, в которых заданы значения некоторой функции  Требуется найти полином степени не выше, такой, чтобы выполнялось условие
Требуется найти полином степени не выше, такой, чтобы выполнялось условие
 (1)
(1)
Будем искать полином в виде
 (2)
(2)
Поступая по аналогии с выводом первой интерполяционной формулы Ньютона, для коэффициентов 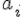 <https://virtet.gsu.by/filter/tex/displaytex.php?a_i> получим следующие выражения
<https://virtet.gsu.by/filter/tex/displaytex.php?a_i> получим следующие выражения
 (3)
(3)
Введем новую переменную  <https://virtet.gsu.by/filter/tex/displaytex.php?+q+=+\frac+{x-x_0}{h}> и, подставляя преобразованные выражения для коэффициентов (3) в соотношение (2), получим первую интерполяционную формулу Гаусса (для интерполирования вперёд)
<https://virtet.gsu.by/filter/tex/displaytex.php?+q+=+\frac+{x-x_0}{h}> и, подставляя преобразованные выражения для коэффициентов (3) в соотношение (2), получим первую интерполяционную формулу Гаусса (для интерполирования вперёд)
 (4)
(4)
Разности  используемые в этой формуле, образуют нижнюю ломаную линию в диагональной таблице разностей 1 (см. далее)
используемые в этой формуле, образуют нижнюю ломаную линию в диагональной таблице разностей 1 (см. далее)
Если полином 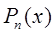 искать в виде
искать в виде

то аналогично (4) можно получить вторую интерполяционную формулу Гаусса (для интерполирования назад)
 (5)
(5)
Разности  , используемые в этой формуле, образуют верхнюю ломаную линию в диагональной таблице разностей 1
, используемые в этой формуле, образуют верхнюю ломаную линию в диагональной таблице разностей 1
Формулы Гаусса применяются для интерполирования в середине таблицы вблизи  . При этом первая формула Гаусса (4) применяется при
. При этом первая формула Гаусса (4) применяется при  , а вторая (5) - при
, а вторая (5) - при 
Таблица 1
Диагональная таблица разностей
 <https://virtet.gsu.by/filter/tex/displaytex.php?x> <https://virtet.gsu.by/filter/tex/displaytex.php?x>  <https://virtet.gsu.by/filter/tex/displaytex.php?y> <https://virtet.gsu.by/filter/tex/displaytex.php?y>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta+y> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta+y>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^2+y> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^2+y>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^3+y> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^3+y>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^4+y> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^4+y>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^5+y> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^5+y>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^6+y> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^6+y>
| |||||||
 <https://virtet.gsu.by/filter/tex/displaytex.php?x_{-4}> <https://virtet.gsu.by/filter/tex/displaytex.php?x_{-4}>  <https://virtet.gsu.by/filter/tex/displaytex.php?y_{-4}> <https://virtet.gsu.by/filter/tex/displaytex.php?y_{-4}>
| |||||||
 <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta+y_{-4}> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta+y_{-4}>
| |||||||
 <https://virtet.gsu.by/filter/tex/displaytex.php?x_{-3}> <https://virtet.gsu.by/filter/tex/displaytex.php?x_{-3}>  <https://virtet.gsu.by/filter/tex/displaytex.php?y_{-3}> <https://virtet.gsu.by/filter/tex/displaytex.php?y_{-3}>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^2+y_{-4}> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^2+y_{-4}>
| |||||||
 <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta+y_{-3}> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta+y_{-3}>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^3+y_{-4}> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^3+y_{-4}>
| |||||||
 <https://virtet.gsu.by/filter/tex/displaytex.php?x_{-2}> <https://virtet.gsu.by/filter/tex/displaytex.php?x_{-2}>  <https://virtet.gsu.by/filter/tex/displaytex.php?y_{-2}> <https://virtet.gsu.by/filter/tex/displaytex.php?y_{-2}>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^2+y_{-3}> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^2+y_{-3}> 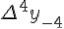 <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^4+y_{-4}> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^4+y_{-4}>
| |||||||
 <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta+y_{-2}> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta+y_{-2}>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^3+y_{-3}> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^3+y_{-3}>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^5+y_{-4}> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^5+y_{-4}>
| |||||||
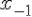 <https://virtet.gsu.by/filter/tex/displaytex.php?x_{-1}> <https://virtet.gsu.by/filter/tex/displaytex.php?x_{-1}>  <https://virtet.gsu.by/filter/tex/displaytex.php?y_{-1}> <https://virtet.gsu.by/filter/tex/displaytex.php?y_{-1}>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^2+y_{-2}> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^2+y_{-2}> 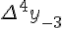 <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^4+y_{-3}> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^4+y_{-3}>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^6+y_{-4}> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^6+y_{-4}>
| |||||||
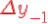 <https://virtet.gsu.by/filter/tex/displaytex.php?\color{red}\Delta+y_{-1}> <https://virtet.gsu.by/filter/tex/displaytex.php?\color{red}\Delta+y_{-1}>  <https://virtet.gsu.by/filter/tex/displaytex.php?+\quad+\\+\searrow> <https://virtet.gsu.by/filter/tex/displaytex.php?+\quad+\\+\searrow>  <https://virtet.gsu.by/filter/tex/displaytex.php?\color{red}+\Delta^3+y_{-2}> <https://virtet.gsu.by/filter/tex/displaytex.php?\color{red}+\Delta^3+y_{-2}>  <https://virtet.gsu.by/filter/tex/displaytex.php?+\quad+\\+\searrow> <https://virtet.gsu.by/filter/tex/displaytex.php?+\quad+\\+\searrow>  <https://virtet.gsu.by/filter/tex/displaytex.php?\color{red}+\Delta^5+y_{-3}> <https://virtet.gsu.by/filter/tex/displaytex.php?\color{red}+\Delta^5+y_{-3}>  <https://virtet.gsu.by/filter/tex/displaytex.php?\quad+\\+\searrow> <https://virtet.gsu.by/filter/tex/displaytex.php?\quad+\\+\searrow>
| |||||||
 <https://virtet.gsu.by/filter/tex/displaytex.php?x_0> <https://virtet.gsu.by/filter/tex/displaytex.php?x_0>  <https://virtet.gsu.by/filter/tex/displaytex.php?y_0> <https://virtet.gsu.by/filter/tex/displaytex.php?y_0>  <https://virtet.gsu.by/filter/tex/displaytex.php?\color{red}+\Delta^2+y_{-1}> <https://virtet.gsu.by/filter/tex/displaytex.php?\color{red}+\Delta^2+y_{-1}>  <https://virtet.gsu.by/filter/tex/displaytex.php?\nearrow+\\+\searrow> <https://virtet.gsu.by/filter/tex/displaytex.php?\nearrow+\\+\searrow> 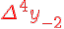 <https://virtet.gsu.by/filter/tex/displaytex.php?\color{red}+\Delta^4+y_{-2}> <https://virtet.gsu.by/filter/tex/displaytex.php?\color{red}+\Delta^4+y_{-2}>  <https://virtet.gsu.by/filter/tex/displaytex.php?\nearrow+\\+\searrow> <https://virtet.gsu.by/filter/tex/displaytex.php?\nearrow+\\+\searrow>  <https://virtet.gsu.by/filter/tex/displaytex.php?\color{red}+\Delta^6+y_{-3}> <https://virtet.gsu.by/filter/tex/displaytex.php?\color{red}+\Delta^6+y_{-3}>
| |||||||
 <https://virtet.gsu.by/filter/tex/displaytex.php?\color{red}+\Delta+y_0> <https://virtet.gsu.by/filter/tex/displaytex.php?\color{red}+\Delta+y_0>  <https://virtet.gsu.by/filter/tex/displaytex.php?\nearrow> <https://virtet.gsu.by/filter/tex/displaytex.php?\nearrow>  <https://virtet.gsu.by/filter/tex/displaytex.php?\color{red}+\Delta^3+y_{-1}> <https://virtet.gsu.by/filter/tex/displaytex.php?\color{red}+\Delta^3+y_{-1}>  <https://virtet.gsu.by/filter/tex/displaytex.php?\nearrow> <https://virtet.gsu.by/filter/tex/displaytex.php?\nearrow>  <https://virtet.gsu.by/filter/tex/displaytex.php?\color{red}+\Delta^5+y_{-2}> <https://virtet.gsu.by/filter/tex/displaytex.php?\color{red}+\Delta^5+y_{-2}>  <https://virtet.gsu.by/filter/tex/displaytex.php?\nearrow> <https://virtet.gsu.by/filter/tex/displaytex.php?\nearrow>
| |||||||
 <https://virtet.gsu.by/filter/tex/displaytex.php?x_1> <https://virtet.gsu.by/filter/tex/displaytex.php?x_1>  <https://virtet.gsu.by/filter/tex/displaytex.php?y_1> <https://virtet.gsu.by/filter/tex/displaytex.php?y_1>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^2+y_0> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^2+y_0>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^4+y_{-1}> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^4+y_{-1}> 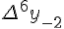 <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^6+y_{-2}> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^6+y_{-2}>
| |||||||
 <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta+y_1> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta+y_1>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^3+y_0> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^3+y_0>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^5+y_{-1}> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^5+y_{-1}>
| |||||||
 <https://virtet.gsu.by/filter/tex/displaytex.php?x_2> <https://virtet.gsu.by/filter/tex/displaytex.php?x_2>  <https://virtet.gsu.by/filter/tex/displaytex.php?y_2> <https://virtet.gsu.by/filter/tex/displaytex.php?y_2>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^2+y_1> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^2+y_1>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^4+y_0> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^4+y_0>
| |||||||
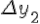 <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta+y_2> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta+y_2>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^3+y_1> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^3+y_1>
| |||||||
 <https://virtet.gsu.by/filter/tex/displaytex.php?x_3> <https://virtet.gsu.by/filter/tex/displaytex.php?x_3>  <https://virtet.gsu.by/filter/tex/displaytex.php?y_3> <https://virtet.gsu.by/filter/tex/displaytex.php?y_3>  <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^2+y_2> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta^2+y_2>
| |||||||
 <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta+y_3> <https://virtet.gsu.by/filter/tex/displaytex.php?\Delta+y_3>
| |||||||
 <https://virtet.gsu.by/filter/tex/displaytex.php?x_4> <https://virtet.gsu.by/filter/tex/displaytex.php?x_4>  <https://virtet.gsu.by/filter/tex/displaytex.php?y_4> <https://virtet.gsu.by/filter/tex/displaytex.php?y_4>
|
Заключение
Преимущество интерполяционной формулы Гаусса состоит в том, что указанный выбор узлов интерполяции обеспечивает наилучшую оценку остаточного члена по сравнению с любым другим выбором, а упорядоченность узлов по мере их близости к точке интерполяции уменьшает вычислительную погрешность интерполирования.