Балтийский федеральный университет имени И. Канта
Физико-технический факультет
| Утверждаю |
| Заведующий кафедры |
| к.т.н., доцент |
| А. Шпилевой |
| «___»_________ 201__ г. |
ЛЕКЦИЯ № 17
Тема: «Шумоподобные сигналы и их использование в системах связи»
Текст лекции по дисциплине: «Теория электрической связи»
| Обсуждена и одобрена на заседании кафедры |
| протокол №___ от «___»___________201__г. |
Г. Калининград 2013 г.
Текст лекции № 28
по дисциплине: «Теория электрической связи»
«Шумоподобные сигналы и их использование в системах связи»
Использование в качестве переносчика информации функций
Уолша
Система функций Уолша – это полная ортогональная система на интервале 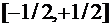 или
или  . Функции Уолша не имеют хороших корреляционных свойств, но обладают свойством ортогональности, что и определяет их практическое применение.
. Функции Уолша не имеют хороших корреляционных свойств, но обладают свойством ортогональности, что и определяет их практическое применение.
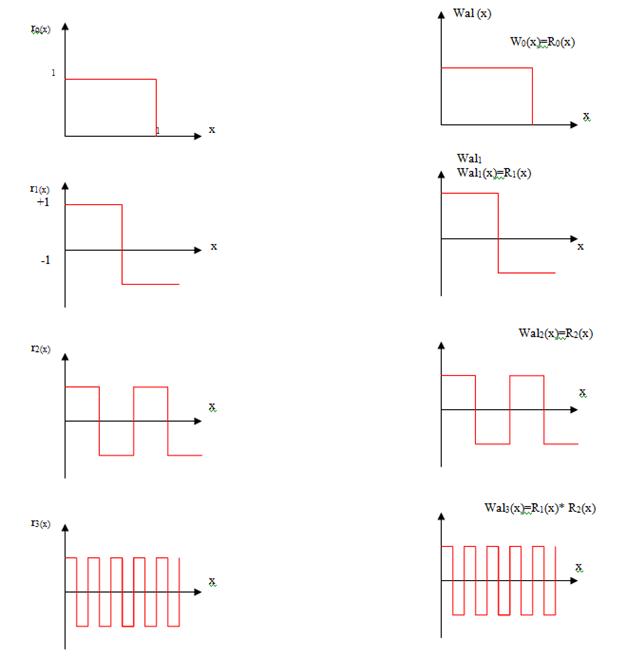
Функции Уолша обычно задаются через функцию Радемахера:
 ; ;
| (1.1) |
 , где аргумент
, где аргумент  – безразмерное время,
– безразмерное время,  – период функции;
– период функции; 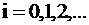 порядок функции.
порядок функции.
Функция знака 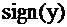 имеет постоянную величину, равную
имеет постоянную величину, равную  , знак которой определяется знаком аргумента
, знак которой определяется знаком аргумента  .
.
 Иначе говоря, функцию Радемахера, принимающую значение
Иначе говоря, функцию Радемахера, принимающую значение  , можно трактовать как функцию «прямоугольного синуса».
, можно трактовать как функцию «прямоугольного синуса».
Система функций Уолша 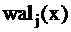 образуется следующим образом:
образуется следующим образом:
1. По определению вводится функция  при
при  .
.
2. Для получения функции 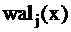 при
при  необходимо j записать в двоичной форме:
необходимо j записать в двоичной форме:
 ; ;
|
 ; ;
|
 ; ;
|
Пример:
1)  ;
;
2)  ,
,  ;
;
3)  ,
,  ;
;
4)  ;
;
5)  ;
;
6) 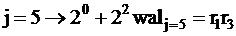 ; и т.д.
; и т.д.
В общем случае выбор ортогональных кодов связан с матрицами Адамара:
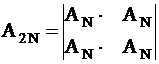 ; ;
| (1.2) |
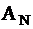 – матрица Адамара порядка
– матрица Адамара порядка  (
( – число равно числу столбцов
– число равно числу столбцов  ).
).
 – матрица Адамара порядка
– матрица Адамара порядка  .
.
Пример: 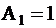
 ; ;
|
 ; ;
|
 ; ;
|
Упорядочим знакоизменение:
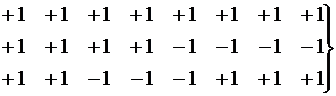 ; и т.д. ; и т.д.
|
т.е. функции Уолша можно задавать через матрицы Адамара.
|
Как доказать ортогональность?
 и
и 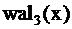

т.е. сигналы (коды) не пересекаются.
Характеристика шумоподобных сигналов
Сложными (шумоподобными) сигналами называют сигналы, у которых база существенно больше 
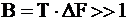 ; ;
| (2.1) |
В последние годы сложные сигналы находят очень широкое применение, в т.ч. в сотовых системах с кодовым разделением сигналов. [CDMA – Code Divisoin Multiple Acces] – множественный доступ с кодовым разделением каналов.
С шириной спектра  в широкополосные сигналы с шириной спектра
в широкополосные сигналы с шириной спектра  при постоянстве энергии
при постоянстве энергии  . (см. рис.)
. (см. рис.)

|
Анализ рис.1:
Пусть необходимо передать сообщение, спектр которого имеет ширину  , а спектральная плотность мощности может быть оценена отношением
, а спектральная плотность мощности может быть оценена отношением  . При использовании ШПС в эфир излучается сигнал с преднамеренно расширенной полосой
. При использовании ШПС в эфир излучается сигнал с преднамеренно расширенной полосой  , так что СПМ энергии исходного сигнала уменьшается в
, так что СПМ энергии исходного сигнала уменьшается в  раз и составляет
раз и составляет  . База сигнала возрастает в
. База сигнала возрастает в  раз.
раз.
Из рисунка видно, что полученный ШПС по отношению к исходному простому представляет шум с приблизительно постоянной в интервале  СПМ. Ясно, что чем больше «растянута» полоса
СПМ. Ясно, что чем больше «растянута» полоса  сложного сигнала при
сложного сигнала при  , тем меньше СП энергии сигнала. В итоге: получившийся ШПС сможет оказать на работающую узкополосную систему сколь угодно малое влияние.
, тем меньше СП энергии сигнала. В итоге: получившийся ШПС сможет оказать на работающую узкополосную систему сколь угодно малое влияние.
Сложные сигналы с большой базой обеспечивают следующие преимущества:
– Высокая помехозащищенность систем связи.
– Эффективная борьба с искажениями в канале связи.
– Одновременная работа многих абонентов в общей полосе частот за счет кодового разделения сигналов.
– Совместимость процессов передачи информации с измерением параметров движения объектов.
– Более эффективное использование спектра частот на ограниченной территории.
Существуют следующие основные типы ШПС:
1. Частотно-модулированные сигналы.
2. Фазоманипулированные сигналы (сигналы с кодовой ФМ).
3. Дискретные частотные сигналы (ШПС на основе ЧВМ).
4. Дискретные составные частотные сигналы.