Лабораторная работа № 7
ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХНЫХ
УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ.
ЗАДАЧА ДИРЕХЛЕ ДЛЯ ПАРАБОЛИЧЕСКОГО УРАВНЕНИЯ
Цель работы
1. Знакомство с методами численного решения дифференциальных уравнений с частными производными в рамках задачи Дирехле.
2. Разработка численной ММ, реализующей один из методов.
3. Оценка точности полученной ММ при помощи средств MATLAB.
Решение дифференциальных уравнений с частными производными (ДУЧП) в аналитическом виде удается только в самых простых случаях. Поэтому становятся особенно важными численные (приближенные) методы решения этих уравнений. Далее будем рассматривать только линейные ДУЧП.
Наиболее широко распространенным и простым методом численного решения линейных ДУЧП является метод сеток или метод конечных разностей, поэтому основной упор сделан на пояснение и описание этого метода.
В общем случае ДУЧП для функции u двух аргументов имеет вид
, (1)
где x, у – независимые переменные, u(x,y) – искомая функция, ux, uy, uxx, uxy, uyy – её первые и вторые частные производные по аргументам x и y.
Решением уравнения (1) называется функция и= u(х, у), обращающая это уравнение в тождество. График решения представляет собой поверхность в пространстве Охуu (интегральная поверхность).
Уравнение (1) называется вполне линейным, если оно первой степени относительно искомой функции и всех ее производных и не содержит их произведений, т. е. если это уравнение может быть записано в виде
, (2)
причем коэффициенты А, В, С, а, b, с могут зависеть лишь от х и у. В частном случае, если эти коэффициенты не зависят от х и у, то уравнение (2) будет линейным дифференциальным уравнением с постоянными коэффициентами. Подробнее рассмотрим линейное дифференциальное уравнения (2).
Пусть D= В2-4АС – дискриминант уравнения. В зависимости от знака функции D линейное дифференциальное уравнение (2) относится в заданной области к одному из следующих типов:
D < 0 – эллиптический тип; D = 0 – параболический тип;
D > 0 – гиперболический тип; D не сохраняет постоянного знака – смешанный тип.
Например, температура и=и(х, t) точки однородного тонкого стержня с абсциссой х для каждого момента времени t удовлетворяет одномерному уравнению теплопроводности
, (3)
где а – постоянная, зависящая от физических свойств стержня, и F(х, y) –функция, связанная с плотностью источников распределения тепла. Если в стержне отсутствуют источники тепла, то уравнение теплопроводности имеет вид
. (4)
Для этого уравнения А=-а2, В=0, С=0 Тогда дискриминант D= В2-4АС =0 поэтому уравнение (3)-(4) парабалического типа
Параболическое уравнение в конечных разностях
Рассмотрим уравнение теплопроводности (4) для стержня 0 ≤ x ≤ l, где для простоты будем полагать а= 1 (к такому случаю всегда можно прийти путем введения нового времени τ=a2t), u=u(х,t) – температура и t – время
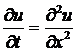. (5)
Пусть в начальный момент времени t=0 задано распределение температуры u(x,0)=f(x) и законы изменения температуры в зависимости от времени (тепловые режимы) на концах стержня х=0 и x=l: u(0,t)=φ(t), u(l,t)=ψ(t).
Требуется найти распределение температуры u=u(х,t) вдоль стержня в любой момент времени t. Решим эту смешанную задачу методом сеток. Для этого рассмотрим пространственно-временную систему координат (х,t) (рис. 1).
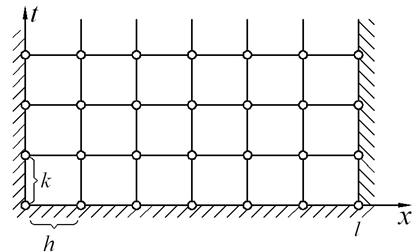
Рис. 1. Прямоугольная сетка
В полуполосе t ≥0, 0 ≤ x ≤ l построим прямоугольную сетку x=ih (i=0, 1,…, n), t=jk (j=0, 1, 2,…), где h=l/n (n – целое) – шаг вдоль оси Ох и k2=σh2 – шаг вдоль оси Ot (σ – постоянная), вообще говоря, различны.
Величина σ будет выбрана ниже. Введя обозначения xi =ih, tj =jk, uij=u(xi, tj) и заменяя уравнение (5) конечно-разностным уравнением, получим:
. (6)
Отсюда
ui,j+1= σ ui-1,j+(1-2σ)uij+ σ ui+1,j. (7)
Из рассмотрения формулы (7) ясно, что зная значения функции u(х,t) в точках j -го слоя t=jk, с помощью этой формулы можно вычислить значения u(х,t) в точках следующего (j+1) -го слоя t=(j+1)k (риc. 2). При вычислении пользуются четырьмя соседними узлами – явная схема вида (рис. 2).
Рис. 2. Явная схема с использованием одного предыдущего слоя j
Таким образом, исходя из начального слоя t=0, значения u(х,t) для которого определяются из начального условия u(xi,0)=f(xi), (i=0, 1,…, n), и используя значения функции u(х,t) в крайних узлах (0, tj), (1, tj) (j=0, 1, 2,…), определяемые граничными условиями u(0,tj)= φ(tj), u(l,tj)= ψ(tj), по формуле (51) последовательно вычисляем: u(xi,t1), u(xi,t2), u(xi,t3),… (i=0, 1,…, n), т. е. находим значения искомой функции u(х,t) во всех узлах полуполосы.
Остается разумно выбрать величину σ. При этом будем исходить из требования, чтобы ошибка при замене дифференциального уравнения (5) конечно-разностным уравнением (6) была наименьшей. Введем обозначения:
, Lh[u]=1/h2[(ui+1,j –2uij+ui-1,j)-1/ σ(ui,j+1 –uij)],
где Lh[u] – конечно-разностный оператор, соответствующий дифференциальному оператору L[u].
Разность Rh[u]=Lh[u]-L[и], называемая ошибкой аппроксимации, есть погрешность, которая получается при замене оператора L[и] оператором Lh[u].
Для Lh[u] можно записать
. (8)
Тогда выберем число σ так, чтобы первая скобка формулы (52) обратилась в нуль, т. е. положим σ/2=1/12 и, следовательно, σ=1/6. При этом значении σ будем иметь
. (9)
При выполнении равенства Rh[u]=Lh[u] при таком выборе σ для погрешности Rh[u] получаем оценку Rh[u]=О(h4), тогда как при другом выборе числа σ имеем Rh[u]=О(h2). В этом смысле значение σ =1/6 является для расчетной схемы 1 наилучшим.
Соответствующая расчетная формула (7) при таком выборе σ окончательно принимает вид
ui,j+1=1/6(ui-1,j+4uij+ui+1,j). (10)
Отметим, что оценка ошибки аппроксимации Rh[u] в общем случае для граничных узлов (xi, tj) не годится.
Порядок выполнения работы
1. Разработать программу для решения смешанной (с начальными и краевыми условиями) задачи для уравнения теплопроводности параболического типа одним из описанных выше методов (например, на алгоритмическом языке Pascal) и провести численное моделирование с получением приближенных (модельных) значений искомых функций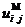 
.
2. Решить эту же задачу средствами MATLAB (пример решения см. в прил.), где в качестве результатов получить экспериментальные («точные») значения искомой функции 
.
3. Оценить точность полученной модели.
Варианты заданий
Задание 7.1. Решить смешанную задачу (задачу Дирехле) для дифференциального уравнения параболического типа (уравнения теплопроводности) 
, при заданных начальных 
и краевых условиях 
, 
, где 
с использованием явной разностной схемы. Решение выполнить при h=0.1 для 
, считая σ =1/6.
Задание 7.2. Решить задачу по пункту 7.1 с использованием неявной разностной схемы методом прогонки.
| № n/n | 
| 
|
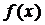
| 0.1 | x*(1-x)*(100*x^19-50*x^10+15*x^2-8*x+2) | |
| 0.2 | x*(1-x)*(100*x^19-50*x^10+15*x^2-8*x+2) | |
| 0.5 | x*(1-x)*(100*x^19-50*x^10+15*x^2-8*x+2) | |
| 0.9 | x*(1-x)*(100*x^19-50*x^10+15*x^2-8*x+2) | |
| 1.5 | x*(1-x)*(100*x^19-50*x^10+15*x^2-8*x+2) | |
| 0.1 | x*(1-x)*(200*x^12-50*x^10+15*x^2-8*x+2) | |
| 0.2 | x*(1-x)*(200*x^12-50*x^10+15*x^2-8*x+2) | |
| 0.5 | x*(1-x)*(200*x^12-50*x^10+15*x^2-8*x+2) | |
| 0.9 | x*(1-x)*(200*x^12-50*x^10+15*x^2-8*x+2) | |
| 1.5 | x*(1-x)*(200*x^12-50*x^10+15*x^2-8*x+2) | |
| 0.1 | x*(1-x)*(300*x^12-30*x^6+15*x^2-8*x+2) | |
| 0.2 | x*(1-x)*(300*x^12-30*x^6+15*x^2-8*x+2) | |
| 0.5 | x*(1-x)*(300*x^12-30*x^6+15*x^2-8*x+2) | |
| 0.9 | x*(1-x)*(300*x^12-30*x^6+15*x^2-8*x+2) | |
| 1.5 | x*(1-x)*(300*x^12-30*x^6+15*x^2-8*x+2) | |
| 0.1 | x*(1-x)*(30*x^8-30*x^6+25*x^4-8*x+2) | |
| 0.2 | x*(1-x)*(30*x^8-30*x^6+25*x^4-8*x+2) | |
| 0.5 | x*(1-x)*(30*x^8-30*x^6+25*x^4-8*x+2) | |
| 0.9 | x*(1-x)*(30*x^8-30*x^6+25*x^4-8*x+2) | |
| 1.5 | x*(1-x)*(30*x^8-30*x^6+25*x^4-8*x+2) | |
| 0.1 | x*(1-x)*(30*x^4-30*x^6+25*x^2-8*x+2) | |
| 0.2 | x*(1-x)*(30*x^4-30*x^6+25*x^2-8*x+2) | |
| 0.5 | x*(1-x)*(30*x^4-30*x^6+25*x^2-8*x+2) | |
| 0.9 | x*(1-x)*(30*x^4-30*x^6+25*x^2-8*x+2) | |
| 1.5 | x*(1-x)*(30*x^4-30*x^6+25*x^2-8*x+2) | |
| 0.1 | x*(1-x)*(30*x^10-30*x^3+25*x^2-8*x+2) | |
| 0.2 | x*(1-x)*(30*x^10-30*x^3+25*x^2-8*x+2) | |
| 0.5 | x*(1-x)*(30*x^10-30*x^3+25*x^2-8*x+2) | |
| 0.9 | x*(1-x)*(30*x^10-30*x^3+25*x^2-8*x+2) | |
| 1.5 | x*(1-x)*(30*x^10-30*x^3+25*x^2-8*x+2) | |
| 0.1 | x*(1-x)*(10*x^7-5*x^6+3*x^5-2*x+2) | |
| 0.2 | x*(1-x)*(10*x^7-5*x^6+3*x^5-2*x+2) | |
| 0.5 | x*(1-x)*(10*x^7-5*x^6+3*x^5-2*x+2) | |
| 0.9 | x*(1-x)*(10*x^7-5*x^6+3*x^5-2*x+2) | |
| 1.5 | x*(1-x)*(10*x^7-5*x^6+3*x^5-2*x+2) | |
| 0.1 | x*(1-x)*(4*x^4-3*x^3+2*x^2-1*x+2) | |
| 0.2 | x*(1-x)*(4*x^4-3*x^3+2*x^2-1*x+2) | |
| 0.5 | x*(1-x)*(4*x^4-3*x^3+2*x^2-1*x+2) | |
| 0.9 | x*(1-x)*(4*x^4-3*x^3+2*x^2-1*x+2) | |
| 1.5 | x*(1-x)*(4*x^4-3*x^3+2*x^2-1*x+2) |