Курсовой проект
по дисциплине
Основы проектирования электронных компонентов базы
на тему:
«Проектирование электронного компонента»
Выполнил:
ст-т гр. Энб-13-3
Макоев Х.О.
Проверил:
Маслаков М.П.
Владикавказ 2016
Содержание
| Задание | |
| Введение | |
| 1 Суммирующий двоичный счетчик с последовательным переносом, собранный на Т-триггерах………………………………………………........ | |
| 1.1Двоичные счетчики………………………………………………….. | |
| 1.2 Двоичные счетчики с параллельным переносом………………….. | |
| 1.3 Счетчики с последовательно-параллельным переносом…………. | |
| 2 Комбинационная схема…………………………………………………….. | |
| 2.1 Построение комбинационной схемы………………………………. | |
| 3 Параллельный регистр, собранный на RS-триггерах…………………….. | |
| 4 Неполный дешифратор с активными единичными сигналами на выходе | |
| 5 Сборка нового элемента…………………………………………………… | |
| Заключение……………………………………………………………………. | |
| Список использованной литературы………………………………………... |
Задание
Вариант №49
Собрать принципиальную электрическую схему по следующей структурной схеме:
Где:
1. Счетчик - суммирующий двоичный счетчик с последовательным переносом, собранный на T-триггерах.
2. Комбинационная схема – построена на основе ДСНФ или КСНФ (если в ДСНФ элементов больше, чем в КСНФ строить на основе нее, если меньше, то на основе КСНФ) по следующей функции:

3. Регистр – параллельный регистр, собранный на RS-триггерах.
4. Дешифратор – не полный дешифратор с активными единичными сигналами на выходе.
Произвести моделирование схемы, сняв характеристики работы, и представить в виде завершенного электронного компонента, полученного в САПР МАХ+ (микросхема).
Введение
Принципиальная схема, принципиальная электрическая схема -графическое изображение (модель), служащее для передачи с помощью условных графических и буквенно-цифровых обозначений (пиктограмм) связей между элементами электрического устройства.
Принципиальные электрические схемы определяют полный состав приборов, аппаратов и устройств (а также связей между ними), действие которых обеспечивает решение задач управления, регулирования, защиты, измерения и сигнализации. Принципиальные схемы служат основанием для разработки других документов проекта: монтажных таблиц щитов и пультов, схем внешних соединений и др.
1 Суммирующий двоичный счетчик с последовательным переносом, собранный на Т-триггерах.
1.1 Двоичные счетчики
Схему двоичного счетчика можно получить с помощью формального синтеза, однако более наглядным путём представляется эвристический. Таблица истинности двоичного счетчика — последовательность двоичных чисел от нуля до 2^n-1, где n - разрядность счётчика. Наблюдение за разрядами чисел, составляющих таблицу, приводит к пониманию структурной схемы двоичного счетчика. Состояния младшего разряда при его просмотре по соответствующему столбцу таблицы показывают чередование нулей и единиц вида 01010101..., что естественно, т. к. младший разряд принимает входной сигнал и переключается от каждого входного воздействия. В следующем разряде наблюдается последовательность пар нулей и единиц вида 00110011.... В третьем разряде образуется последовательность из четверок нулей и единиц 00001111... и т.д. Из этого наблюдения видно, что следующий по старшинству разряд переключается с частотой, в два раза меньшей, чем данный.
Известно, что счетный триггер делит частоту входных импульсов на два. Сопоставив этот факт с указанной выше закономерностью, видим, что счетчик может быть построен в виде цепочки последовательно включенных счетных триггеров.
1.2 Двоичные счетчики с параллельным переносом
Выше рассмотрены схемы двоичных последовательных счетчиков, то есть таких счетчиков, в которых при изменении состояния определенного триггера возбуждается последующий триггер, причем триггеры меняют свои состояния не одновременно, а последовательно. Если в данной ситуации должны изменить свои состояния n триггеров, то для завершения этого процесса потребуется n интервалов времени, соответствующих времени изменения состояния каждого из триггеров. Такой последовательный характер работы является причиной двух недостатков последовательного счетчика: меньшая скорость счета по сравнению с параллельными счетчиками и возможность появления ложных сигналов на выходе схемы. В параллельных счетчиках синхронизирующие сигналы поступают на все триггеры одновременно.
Последовательный характер переходов триггеров счетчика является источником ложных сигналов на его выходах. Например, в счетчике, ведущем счет в четырёхразрядном двоичном коде с «весами» 8-4-2-1, при переходе от числа 7_{10} = 0111_2 к числу 8_{10} = 1000_2 на выходе появится следующая последовательность сигналов:
0111 ->ð 0110 ->ð 0100 ->ð 0000 ->ð 1000
Это означает, что при переходе из состояния 7 в состояние 8 на входах счетчика на короткое время появятся состояния 6; 4; 0. Эти дополнительные состояния могут вызвать ложную работу других устройств, например, если к такому счетчику подключён дешифратор, то на его выходах 0, 4, 6 могут кратковременно возникнуть активные состояния, которые могут ложно изменить состояния подключенных к ним триггеров — это явление называется логическими «гонками» или «гонками сигналов». Исключить гонки можно, применяя счетчики с соседним или противогоночным кодированием состояний, например, считающие в рефлексивном коде Грея.
С целью уменьшения времени протекания переходных процессов можно реализовать счетчик в варианте с подачей входных импульсов одновременно на все триггеры. В этом случае получим счетчик с параллельным переносом.
По схемам счетчиков всегда строятся счетчики, задержка переключения одного триггера у которых соизмерима с периодом считаемых импульсов. Пример. Задержка переключения одного триггера 30 нс, и если мы построим счетчик более, чем 4-хразрядный, то при периоде счетных импульсов 120 нс могут начаться сбои счета, перенос не успевает распространиться по цепочке триггеров до прихода очередного счетного импульса.
Здесь на информационные входы триггеров подаются сигналы, являющиеся логической функцией состояния счетчика и определяющие конкретные триггеры, которые изменяют своё состояние при данном входном импульсе. Принцип стробирования сводится к следующему: триггер меняет своё состояние при пропускании очередного импульса синхронизации, если все предыдущие триггеры находились в состоянии логической единицы.
Параллельные счетчики имеют более высокое быстродействие по сравнению с последовательными, поскольку синхронизирующие импульсы поступают на все триггеры одновременно.
1.3 Счетчики с последовательно-параллельным переносом
В связи с ограничениями на построение счетчиков с параллельным переносом большой разрядности широкое распространение получили счетчики с групповой структурой, или счетчики с последовательно-параллельным переносом. Разряды таких счетчиков разбиваются на группы, внутри которых организуется принцип параллельного переноса. Сами же группы соединяются последовательно с использованием конъюнкторов, формирующих перенос в следующую группу при единичном состоянии всех триггеров предыдущих. При единичном состоянии всех триггеров группы приход очередного входного сигнала создаст перенос из этой группы. Эта ситуация подготавливает межгрупповой конъюнктор к прямому пропусканию входного сигнала на следующую группу.
В наихудшем для быстродействия случае, когда перенос проходит через все группы и поступает на вход последней,
tУСТ = t • (ĺ — 1) + tГР,
где ĺ — число групп, tГР — время установления кода в группе.
В развитых сериях ИС обычно имеется по 5…10 вариантов двоичных счетчиков, выполненных в виде 4-хразрядных групп (секций). Каскадирование секций может выполняться путём их последовательного включения по цепям переноса, организации параллельно-последовательных переносов или для более сложных счетчиков с двумя дополнительными управляющими входами разрешения счета и разрешения переноса путём организации параллельных переносов и в группах, и между ними.
Особенностью двоичных счетчиков синхронного типа является наличие ситуаций с одновременным переключением всех его разрядов (например, для суммирующего счетчика при переходе от кодовой комбинации 11…1 к комбинации 00…0 при переполнении счетчика и выработке сигнала переноса). Одновременное переключение многих триггеров создает значительный токовый импульс в цепях питания ЦУ и может привести к сбою в их работе. Поэтому в руководящих материалах по использованию некоторых БИС/СБИС программируемой логики, в частности, имеется ограничение на разрядность двоичных счетчиков заданной величиной k. При необходимости применения счетчика большей разрядности рекомендуется переходить к коду Грея, для которого переходы от одной кодовой комбинации к другой сопровождаются переключением всего одного разряда. Правда, для получения результата счета в двоичном коде придется использовать дополнительно преобразователь кода, но это является платой за избавление от токовых импульсов большой интенсивности в цепях питания.
Счётчики с последовательным переносом, это счётчики, в которых переключение триггеров разрядных схем осуществляется последовательно один за другим.

Рисунок 1 - Схема суммирующего двоичного счетчика с последовательным переносом, собранного на Т-триггерах

Рисунок 2 - Временные диаграммы, характеризующие работу счетчика

Рисунок 3 - Графическое изображение полученной модели счетчика
Комбинационная схема
Комбинационные схемы - это схемы, у которых выходные сигналы Y = (у1, у2,..., уm) в любой момент дискретного времени однозначно определяются совокупностью входных сигналов Х = (х1, х2,..., хn), поступающих в тот же момент времени t. Реализуемый в КС способ обработки информации называется комбинационным потому, что результат обработки зависит только от комбинации входных сигналов и формируется сразу при поступлении входных сигналов. Поэтому одним из достоинств комбинационных схем является их высокое быстродействие. Преобразование информации однозначно описывается логическими функциями вида Y=f(Х). Логические функции и соответствующие им комбинационные схемы подразделяют на регулярные и нерегулярные структуры. Регулярные структуры предполагают построение схемы таким образом, что каждый из ее выходов строится по аналогии с предыдущими. В нерегулярных структурах такая аналогия отсутствует. Многие регулярные структуры положены в основу построения отдельных ИС малой и средней степени интеграции или отдельных функциональных частей БИС и СБИС. Из регулярных комбинационных схем наиболее распространены дешифраторы, шифраторы, схемы сравнения, комбинационные сумматоры, коммутаторы и др.
Для построения любой КС необходима таблица истинности ее функционирования (составляется или задается), затем составляется функция зависимости каждого выхода схемы от входа (в форме СДНФ, которую затем можно перевести в упрощенную форму) и производится построение схемы на определенных логических элементах (чаще всего на И-НЕ и ИЛИ-НЕ). Как правило, построение и расчет любой схемы осуществляется, начиная с ее выхода.
Построение комбинационной схемы
 ;
;
Таблица 1 – Таблица истинности для функции  .
.
| x1 | x2 | x3 | x4 | a | b | c | d | e | f | g | h |
a=  ;
;
b=  ;
;
c=  ;
;
d= 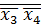 ;
;
e= 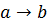 ;
;
f=  ;
;
g=  ;
;
h=  ;
;
Так как ложных значений у функции больше, чем истинных, то находим КСНФ и по ней строим комбинационную схему.

Рисунок 4 - Комбинационная схема

Рисунок 5 - Временные диаграммы, характеризующие работу комбинационной схемы

Рисунок 6 - Графическое изображение полученной модели комбинационной схемы