Предварительные результаты олимпиады на сайте olymp.omich.net
Просмотр работ участников олимпиады и апелляция 26 декабря, в 9-30, ауд. 301. Награждение победителей в 10-30.
Математическая олимпиада школьников
имени Г.П. Кукина
19.12.10 · 9 класс
г. Омск
Математическая олимпиада ОмГУ носит имя профессора Г.П. Кукина, создателя системы городских математических олимпиад.
1. Числа x, y и z подобраны так, что выполнены равенства  . Какие значения может принимать величина
. Какие значения может принимать величина  ?
?
2. Высота АН и биссектриса СК треугольника АВС разбивают его на четыре части, две из которых равнобедренные треугольники. Найдите отношение АС/BC.
3. Сумма трёх натуральных чисел (не обязательно различных) делится на каждое из этих чисел. Какие значения может принимать эта сумма? Объясните, почему другие значения невозможны.
4. В равнобедренном треугольнике вписанная окружность касается основания АВ в точке F, а боковых сторон ВС и АС в точках D и Е соответственно. Отрезок AD пересекает окружность в точке Q. Докажите, что прямая EQ делит отрезок AF пополам.
5. Каждая клетка клетчатого квадрата 2010×2010 покрашена в синий или красный цвет. Известно, что в каждом столбце синих и красных клеток поровну и в каждой строке синих и красных клеток поровну. Докажите, что найдутся две клетки одного цвета, симметричные относительно центра.
6. Есть прибор, который за одно испытание для любых 5 камней определяет среди них средний по весу. Как найти средний из 7 камней разного веса не более чем за 5 испытаний?
Предварительные результаты олимпиады на сайте olymp.omich.net
Просмотр работ участников олимпиады и апелляция 26 декабря, в 9-30, ауд. 301. Награждение победителей в 10-30.
Класс. Решения задач.
1.  Ответ. 0 или 2.
Ответ. 0 или 2.
Решение. Запишем исходное двойное равенство в виде системы  Преобразуем ее к виду
Преобразуем ее к виду  , откуда следует, что:
, откуда следует, что:
 или
или  или
или  или
или 
Если  то
то 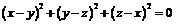 .
.
Если  то
то  но тогда
но тогда 
Если  то
то  но тогда
но тогда 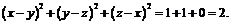
Если  то
то  но тогда
но тогда 
2. Точку пересечения АН и СК назовем О. Предположим, что равнобедренным является треугольник ОНС. В таком случае, получаем, что ÐНСО=ÐНОС=45°. Но тогда ÐАСВ=2ÐНСО=90°, а тогда бы АН совпала с АС, но по условию задачи это не так. Поэтому треугольник ОНС не может быть равнобедренным. Поэтому равнобедренные треугольники – это АОС и АОК. Заметим, что угол НОС – острый (поскольку это один из углов прямоугольного треугольника, не равный 90°). Поэтому угол АОС тупой и в треугольнике АОС ÐОАС=ÐОСА. Рассмотрим треугольник АНС. В нем угол НСА вдвое больше, чем угол НАС, поэтому угол НСА=60°, а угол НАС=30°. Поэтому угол АОК тоже равен 60°. Но, если в равнобедренном треугольнике один из углов равен 60°, этот треугольник равносторонний. Поэтому в треугольнике КАО все углы по 60°. Тогда в исходном треугольнике АВС ÐА=90°, ÐС=60°, ÐВ=30° и АС/ВС=1/2.
3. Ответ. Все числа, делящиеся на 3 и все числа, делящиеся на 4.
Решение. Все такие числа заведомо годятся. Например, можно взять тройки { a, a, a } и { a, a, 2 a }. Докажем, что другие числа получиться не могут. Пусть a, b, c – данные натуральные числа. По условию a + b + c делится на a, но тогда b + c делится на a, аналогично a + c делится на b, a + b делится на  . Упорядочим числа: без ограничения общности можно считать, что
. Упорядочим числа: без ограничения общности можно считать, что  Но тогда сумма
Но тогда сумма  при делении на с может давать в частном только 1 или 2. Рассмотрим оба варианта. В первом случае a + b = c, причем a + c =2 a + b делится на
при делении на с может давать в частном только 1 или 2. Рассмотрим оба варианта. В первом случае a + b = c, причем a + c =2 a + b делится на  , тогда
, тогда  делится на
делится на  . Но так как
. Но так как  , то либо a = b, либо 2 a = b. Тогда либо a + b + c =4 a, либо a + b + c =6 a. Во втором случае a + b =2 c и a + b + c=3с. В любом случае сумма делится либо на 4, либо на 3.
, то либо a = b, либо 2 a = b. Тогда либо a + b + c =4 a, либо a + b + c =6 a. Во втором случае a + b =2 c и a + b + c=3с. В любом случае сумма делится либо на 4, либо на 3.
4. Пусть прямая  пересекает отрезок
пересекает отрезок  в точке
в точке  . Докажем, что
. Докажем, что  . По теореме о квадрате касательной
. По теореме о квадрате касательной  . Так как
. Так как  и
и  - точки касания вписанной окружности, то
- точки касания вписанной окружности, то  , тогда прямая ED параллельна АВ, а значит
, тогда прямая ED параллельна АВ, а значит  как накрест лежащие. Угол
как накрест лежащие. Угол  , образованный касательной и хордой, равен вписанному
, образованный касательной и хордой, равен вписанному  и равен
и равен  . Но тогда треугольники
. Но тогда треугольники 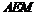 и
и 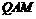 подобны по двум углам (
подобны по двум углам ( ,
,  - общий), а значит
- общий), а значит  , т.е.
, т.е.  , откуда следует, что
, откуда следует, что  .
.
5.  Предположим противное. Тогда в каждой паре клеток, симметричных относительно центра, одна синяя, другая – красная. Разобьем квадрат 2010×2010 на 4 квадрата 1005×1005 (см. рисунок) и занумеруем их.
Предположим противное. Тогда в каждой паре клеток, симметричных относительно центра, одна синяя, другая – красная. Разобьем квадрат 2010×2010 на 4 квадрата 1005×1005 (см. рисунок) и занумеруем их.
Пусть в квадрате № 1  красных клеток и
красных клеток и  синих. Каждой красной клетке квадрата № 1 соответствует синяя клетка квадрата № 4 (и наоборот), тогда в квадрате № 4
синих. Каждой красной клетке квадрата № 1 соответствует синяя клетка квадрата № 4 (и наоборот), тогда в квадрате № 4  красных клеток и
красных клеток и  синих. Аналогично: если в квадрате № 2
синих. Аналогично: если в квадрате № 2  красных клеток и
красных клеток и  синих, то в квадрате № 3
синих, то в квадрате № 3  красных клеток,
красных клеток,  синих.
синих.
По условию в каждом столбце синих и красных клеток поровну и в каждой строке синих и красных клеток поровну, тогда суммарное количество красных клеток в квадратах № 1 и 2 равно суммарному количеству красных клеток в квадратах № 3 и 4. Имеем  , откуда
, откуда  . Аналогично суммарное количество красных клеток в квадратах № 1 и 3 равно суммарному количеству красных клеток в квадратах № 2 и 4, т.е.
. Аналогично суммарное количество красных клеток в квадратах № 1 и 3 равно суммарному количеству красных клеток в квадратах № 2 и 4, т.е.  , а значит
, а значит 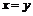 , что противоречит условию
, что противоречит условию  (
( - нечетное число).
- нечетное число).
6. Решение. Основную роль играет следующее простое соображение: если камень оказался средним среди каких-то пяти, то во всей группе он либо 3-й, либо 4-й, либо 5-й по весу. Будем делать так. Отложим любые 2 камня, найдем средний из остальных, заменим его на один из отложенных камней, найдем средний из новых пяти, заменим и его на последний отложенный,и снова найдем средний. Теперь есть три средних камня (3-й, 4-й и 5-й) p, q, r и четыре других a, b, c, d, среди них два легких (легче средних) и два тяжелых (тяжелее средних). Испытаем один раз a, b, p, q, r, другой раз p, q, r, c, d. Если пара (a, b) состоит из легкой и тяжелой, то пара (c, d) – тоже, и средним оба раза окажется средний из семи камней. Если пары (a, b) и (c, d) одна легкая, другая тяжелая, то средними в испытаниях окажутся разные камни (пятый и третий). Значит если в двух этих пятёрках средний один и тот же, то он искомый. А если разные, то нужно брать оставшийся из средней группы.
Критерии проверки (из расчета 7 баллов за задачу)
1. Приведено верное решение, получены оба варианта ответа – 7 баллов. Преобразование исходных равенств выполнено, верно, получено разложение на множители, но при переборе возможностей некоторые случаи потеряны – до 2 баллов. В противном случае – 0 баллов.
2. Задача решена верно – 7 баллов. Равенство высот треугольника доказано, но вывод о равенстве сторон приведен без обоснования – 6 баллов. В противном случае – 0 баллов.
3. Приведено верное решение, в ответе указаны оба множества чисел, доказано, что другие значения сумма принимать не может – 7 баллов. Приведены примеры троек натуральных чисел, откуда следует, что сумма этих трех чисел может принимать любые значения, кратные 3, или любые значения, кратные 4, но не доказано, что других возможностей нет – до 2 баллов. В противном случае – 0 баллов.
4. Задача решена верно – 7 баллов. Доказано равенство углов, из которых следует подобие треугольников 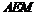 и
и 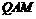 , но дальнейших продвижений нет – 2 балла. В противном случае – 0 баллов.
, но дальнейших продвижений нет – 2 балла. В противном случае – 0 баллов.
5. Приведено верное решение, в каком-либо виде использующее идею четности – 7 баллов. Имеется доказательство, что утверждение задачи верно для квадрата меньшего размера (например, 6×6), которое может быть обобщено для квадрата 2010×2010 – до 4 баллов. В противном случае – 0 баллов.
6.