Неопределенный интеграл.
Дифференциальное исчисление решает следующую задачу: дана функция F(x),найти ее производную f(x).
 F′(x) = f(x).
F′(x) = f(x).
найти
Интегральное исчисление решает обратную задачу: дана функция f(x), найти такую функцию F(x), производная от которой равна f(x). 
 F′(x) = f(x)
F′(x) = f(x) 

Дана
Определение. Первообразной от функции f(x) называется такая функция F(x), производная которой равна f(x).
Например, f(x) = 3x2, тогда F(x) = x3, (x3)′ = 3x2. В качестве первообразной можно взять любую функцию вида x3 + C, т.к. (x3 + C)′ = 3x2.
Теорема. Если функция имеет первообразную, то она имеет и бесконечное множество первообразных, причем любые две из них отличаются лишь постоянным слагаемым.
Пусть F(x) и Φ(x) – любые две первообразные. Рассмотрим Θ(x) = F(x) – Φ(x). Докажем, что Θ(x) ≡ Const.
Найдем Θ′(x) = F′(x) - Φ′(x) ≡ 0. Рассмотрим два значения аргумента a и х (а – фиксированное, х – произвольное).

Определение. Множество всех первообразных функции f(x) называется неопределенным интегралом.
∫f(x)dx.
Если f(x) – первообразная f(x), то
∫f(x) dx = F(x) + C.
Свойства неопределенного интеграла.

Таблица основных интегралов.



 П р и м е р ы.
П р и м е р ы.
1. ∫dx = x + C.


Основные методы интегрирования.
Метод подстановки.
Теорема. Если ∫ f(u)du = F(u) + C и u = φ(x) – любая дифференцируемая функция от x, то
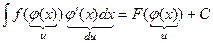
Доказательство. (F(φ(x)) + C)′ = F′(φ(x))∙φ′(x) = f(φ(x))∙φ′(x), т.к. F′(x) = f(x).
Следствие. Если ∫ f(x)dx = F(x) + C, то ∫ f(kx)dx = 1/k F(kx) + C,
∫ f(kx + b)dx = 1/k F(kx + b) + C.
Эта теорема позволяет расширить возможности таблицы основных интегралов. В этой таблице под u можно понимать любую функцию х.
П р и м е р ы.
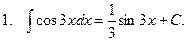




Интегралы от некоторых функций, содержащих квадратный трехчлен.
1. 


Интегрирование по частям.
В интегрировании нет теоремы об интеграле произведения. В какой-то степени ее заменяет формула интегрирования по частям.
Пусть u и v - дифференцируемые функции х. Тогда
d(uv) = du v + u dv или udv = d(uv) – vdu
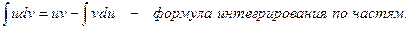
Формула интегрирования по частям применяется в следующих случаях:
1.  где
где
Pm(x) = a0xm + a1xm-1 +….+ am-1 x + am,
u = Pm(x), dv = все остальное.
2. 
П р и м е р ы.

Иногда интегрирование по частям приходится применять несколько раз.




Интегралы от некоторых тригонометрических выражений.


3. 

Рациональные дроби.
Рациональной дробью называется дробь вида
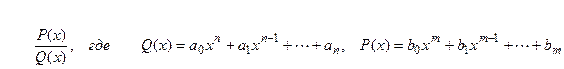
Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя ( m < n). В противном случае дробь называется неправильной.

Неправильная дробь путем деления числителя на знаменатель представляется в виде суммы многочлена и правильной дроби.
Эта операция называется выделением целой части.







Простейшие рациональные дроби.

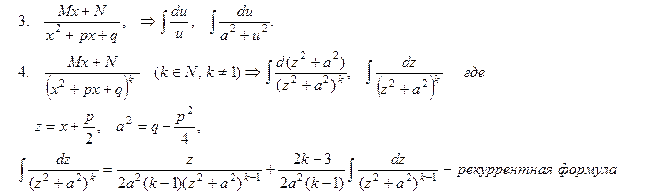
Некоторые сведения из алгебры.
Q(x) = a0 xn + a1xn-1 +... + an-1 x + an (1)
1. Основная теорема высшей алгебры. Всякий многочлен степени n имеет n корней, действительных или комплексных.
2. Если корни многочлена действительны, то каждому комплексному корню соответствуетдругой комплексный корень, с ним сопряженный.
Н а п р и м е р Q(x) = x3 + 2x2 + 2x.
 Q(x) = x (x2 + 2x + 2), x1 = 0, x2,3 = -1 ± √ 1 – 2 = -1 ± i
Q(x) = x (x2 + 2x + 2), x1 = 0, x2,3 = -1 ± √ 1 – 2 = -1 ± i
3. Если x1, x2, …. xn – корни многочлена (1), то многочлен представляется в виде
Q(x) = a0(x – x1) (x – x2).... (x – xn) (2)
4. Пусть x1 = x2 = …. = xk = b – k корнеймногочлена одинаковы. Тогда в разложение (2) входит множитель (x – b)k (b – корень кратности k)
5. Пусть α ± β i – пара комплексных сопряженных корней. Тогда в разложение (2) входит пара множителей
(x – α - β i) (x – α + β i) = (x – α)2 – β2 i2 = x2 – 2 α x + α2 + β 2 = x2 + px + q,
где p = -2 α, q = α2 + β2 – квадратный трехчлен, не разлагающийся на действительные множители.
6. Если α + β I и α - β I - корни кратности l, то в разложение входит множитель
(x − α − β i)l (x − α + β i)l = (x2 – px + q)l
На основании этого многочлен (1) запишется в виде

(3) – разложение многочлена (1) на простейшие действительные множители,
к1 + k2 +… + kr + 2l1 + 2l2 + … + 2ls = n
П р и м е р.
x5 – 2x3 – 8x = x(x2 + 2) (x2 – 4) = x(x2 +2) (x – 2) (x + 2).
Теорема о разложении правильной рациональной дроби на простейшие. 

где Q(x) представляется в виде (3).
Данная дробь представляется как сумма простейших следующим образом
