Передаточные функции W2(p), W3(p), W4(p), W5(p), W6(p), W7(p), W8(p), W9(p) известны по аналогам [2]. Раскроем математические модели этих звеньев.
Передаточная функция выхлопной трубы W2(p):
y2(t) =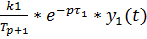 
,
где: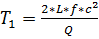 
;
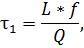
c=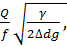 
где: γ – удельный вес;
L – длина участка;
d – диаметр трубы;
f – площадь сечения трубы;
∆d – перепад давления.
Математическая модель измерительного устройства концентрации CO представлена выражением W3(p):
y3(t) =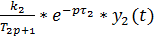 
Для измерения ЗВ, могут быть использованы измерительные преобразователи различного принципа действия и конструкции, имеющие соответствующие значения параметров передаточной функции [2].
Математическая модель передающего устройства, расположенная на автомобиле представлена выражением W5(p):
y4(t) = 
Математическая модель принимающего устройства представлена выражением W5(p):
y5(t) =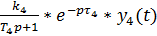 
Математическая модель устройства, выполняющего обработку и обратную передачу сигналов со стороны ГЛОНАСС, после сравнивающего устройства представлена выражением W6(p):
y6(t) =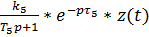 
z(t) = y5(t) – y*50(t),
где: y*(t) – допустимое значение концентрации ЗВ на выходе с измерительного устройства.
Математическая модель приемника со стороны автомобиля W7(p):
y7(t) = 
Математическая модель управляющего устройства ПИД-регулятор, W8(p):
u(t)= W8(p)*y7(t)
u(t) = (k7+k8p+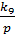 
*)y7(t)
Математическая модель исполнительного устройства (нагревателя) W9(p):
u1(t) = 
В качестве нагревателя предлагается нагреватель, встроенный в катализатор системы EMICAT, применяемый в BMW Alphina B1257, AUDI [4].
Построение математической модели катализатора требует рассмотрения реакторов, применяемых в равном случае:
- реакторы с промежуточным отводом (подводом) тепла – многослойные (полочные) аппараты;
- реакторы с непрерывным отводом (подводом) тепла – трубчатые аппараты.
Их схемы показаны на рисунке 2.3.
Рисунок 2.3 - Основные типы каталитических реакторов с неподвижным слоем
Так же, применяются различные конструкции с более сложными способами отвода (подвода) тепла, например, комбинированные схемы.
· Адиабатический реактор – это металлический цилиндр, в нижней части которого находится решетка, на нее насыпается катализатор в виде различного типа гранул (шариков, зёрен неправильной формы, таблеток и т.д.). Стенки цилиндра теплоизолированы
· Многослойный реактор - это реактор с несколькими адиабатическими слоями катализатора и промежуточным отводом тепла между ними. Отвод тепла может осуществляться с помощью встроенных или выносных теплообменников, или добавлением холодной исходной газовой смеси между слоями
· В трубчатом реакторе отвод тепла осуществляется путем теплообмена реагирующей смеси с теплоносителем через стенку реактора. Катализатор загружается в трубки (их диаметр составляет 2-8 см), а в межтрубном пространстве циркулирует теплоноситель - водяной пар под давлением или расплав солей.
Стоимость таких аппаратов значительно повышается, из-за сложной конструкции.
· Комбинированные реакторы - это трубчатые реакторы, дополненные адиабатическими слоями катализатора. Присутствие адиабатических слоев позволяет осуществить допревращение оставшегося исходного вещества при более высокой температуре по сравнению с трубчатым реактором. Это происходит в силу того, что на выходе из трубчатой части реактора концентрации исходного реагента и тепловыделение уже невысоки. В итоге при меньшей загрузке катализатора достигается высокая производительность.
Степень детализации модели может быть различной, характер детализации зависит от того, на какие вопросы желательно получить ответ. Для многих среднеэкзотермических процессов массо- и теплообмен между газовым потоком и наружной поверхностью зёрен катализатора достаточно интенсивен, температура и концентрации на внешней поверхности зерна катализатора равны температуре и концентрациям в потоке. В этом случае для описания каталитического процесса в реакторе квазигомогенную однофазную модель.
Существуют различные подходы к построению математический моделей процессов, протекающих в катализаторе.
Каталитический процесс в реакторе рассматривается при следующих допущениях:
- продольный перенос массы и тепла не сказывает существенного влияния на градиенты концентраций и температур по высоте слоя;
- коэффициенты диффузии и теплопроводности меняются незначительно по радиусу слоя;
- скорость газового потока и теплоемкость газовой среды постоянна по высоте и сечению реактора.
Математическая модель реактора в этом случае имеет следующий вид:
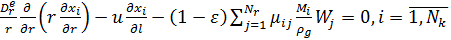(2.1)
(2.2)
Граничные условия:
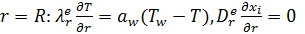(2.3)
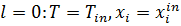
где: Dre - коэффициент диффузии по радиусу трубки;
u - линейная скорость на полное сечение трубки;
ε – прозрачность слоя (доля свободного объема слоя);
Mi -молекулярный вес i-го вещества в j-й реакции;
ρg –плотность газовой смеси;
μij- стехиометрический коэффициент i-го вещества d j-й реакции;
pg - плотность газовой смеси;
Nr - число реакций;
Nk - число ключевых веществ;
Wi - наблюдаемая скорость образования (расходования) i-го вещества, отнесённая к единице объёма зерна (с учетом диффузионного торможения реакции);
xi, xiin - концентрация i-го вещества в слое и на входе в слой;
λre - эффективный коэффициент теплопроводности по радиусу трубки;
cp- теплоемкость газовой смеси;
Qj - тепловой эффект j-й реакции;
Т, Tw, Tin - температура слоя катализатора, хладоагента и исходной реакционной смеси соответственно;
αw - коэффициент теплообмена с холодильником;
1 - координата по длине трубки;
r - координата по радиусу трубки;
R - радиус трубки.
В [] приведены уравнения каталитического процесса в другой форме:
, 
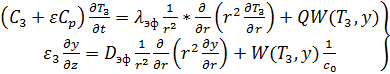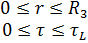(2.4)
(2.5)
(2.6)
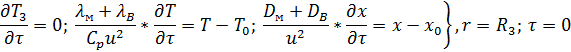
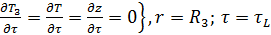(2.7)
где: T3, T, TH, T0 - температура в зоне катализатора, в свободном объеме слоя, начальная (при t = 0) и входная соответственно;
х, у- степени превращения исходного вещества в свободном объеме слоя и в зоне соответственно;
C0 - начальная концентрация исходного вещества;
Sуд - удельная наружная поверхность зерен катализатора, отнесенная к единице объема слоя, для слоя, состоящего из шаров Sуд = 3(1 — ε)/R3;
L – длина слоя катализатора;
λск - эффективный коэффициент продольной теплопроводности в скелете (каркасе) слоя;
ε - пористость слоя катализатора; τ = l/u - условное время контакта;
τL = L/u; l - текущая длина слоя.
Переход от уравнений 2.1 - 2.7 к передаточной функции W1(p) представляется достаточно сложным. В то же время можно построить W1(p) исходя из кинетики реакций, которые происходят в катализаторе за время его работы. В автомобилях устанавливаются разные катализаторы – как реагирующие вещество может использоваться либо платина, либо золото. Устройства, использующие золото значительно дешевле, но качество и срок службы так же значительно уступают платиновым. В рассматриваемом случае считаем, что в результате прохождения составляющей ВВГ происходит каталитическая реакция следующего вида:
,
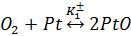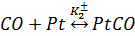, (2.8)
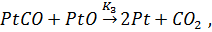
где: O2 – молекулярный кислород;
CO – монооксид углерода;
CO2 - диоксид углерода;
Pt – платина (выступающая в роли катализатора);
PtO, PtCO – промежуточные вещества;
K1±, K2±, K3 – константы при постоянной температуре скорости реакции.
Введем следующие обозначения:
μ, v – концентрации промежуточных веществ на поверхности платины PtO и PtCO, соответственно.
Напомним, что W1(p) должна связывать изменение температуры нагревателя катализатора с количеством CO*, поступающего с его выхода оставшегося после превращения CO в CO2 на входе катализатора.
Константы скорости Ki± зависят от температуры по закону Аррениуса и определяются на основании экспериментальных данных. На сегодняшний день значения следующие:
,
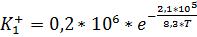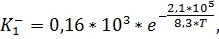
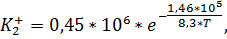
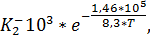
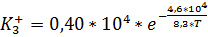. (2.9)
Уравнение Аррениуса имеет вид:
(2.10)
где:K- константа скорости реакции;
А- масштабный множитель;
E – энергия активации;
R- универсальная газовая постоянная = 8, 3 (Дж/моль*К);
T – температура в кельвинах.
Обратим внимание на то, что в системе химических уравнений монооксид углерода и диоксид углерода участвуют в равном молярном соотношении.
Поскольку скорость увеличения количества CO2 эквивалентна скорости убывания CO, то для ускорения нейтрализации монооксида углерода необходимо увеличить скорость реакции диоксида углерода (в уравнении 3 системы 2.8) образования СО2).
Скорость изменения концентрации CO2,будет:
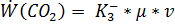. (2.11)
Следовательно, чем больше константа скорости, тем выше скорость образования CO2, и выше скорость перехода CO в CO2
Известно также, что температуру и скорость реакции связывает уравнение Ван-Гоффа:
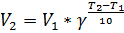, (2.12)
где: V2 – скорость реакции при температуре T2;
V1- скорость реакции при температуре T1;
γ – температурный коэффициент;
γ = k3.
Если температурный коэффициент равен 2, то скорость реакции будет увеличиваться в 2 раза, при повышении температуры на 10 градусов.
Однако, уравнение 2.12 применимо только для реакций протекающих при температуре 0 – 100 ˚С, что не соответствует работе автомобильного катализатора. Поэтому зависимость К3 (T˚) принимается по закону Аррениуса:
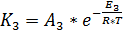, (2.13)
где: T˚=F(t), т.е. является функцией времени t.
Все величины в уравнении 2.13кроме Т˚, постоянные и известные. На рисунке 2.5 изображен график зависимости К3 от Т˚ (график построен в среде Maple 11).
Рисунок 2.4 - Зависимость К3 от изменения температуры
Таким образом, скорость изменения концентрации в уравнении 2.11 принимает следующий вид:
.
Произведем подстановку полученного коэффициента в уравнении 2.11:
.
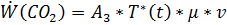C учетом того, что отмечалось ранее, можно считать что с такой скоростью происходит на образование CO2 и эквивалентное убывание CO. Тогда получаем итоговую зависимость:
.
Введем оператор Лапласа 
, тогда получим,
.
Сделав необходимые преобразования получим передаточную функцию W1СО*(p) (зависимость нейтрализуемой концентрации от температуры) в виде
Концентрации M и V можно усреднить, так как в процессе реакций соотношение концентраций абсорбирующих веществ, стабильно.
Уточнение передаточной функции W1(p) возможно после идентификации катализатора известными частотными или временными методами.
Результаты моделирования были получены с помощью программного пакета Mathlab Simulink.
Передаточные функции представлены блоками. После сравнивающего устройства стоит ограничитель сигнала - чтоб сигнал меньше нуля дальше не проходил (т.к. при запуске модели до момента, когда сигнал достигнет СУ на выход идет -0.1). За ПИД-регулятором установлено звено запаздывания вносимого экстраполятором нулевого порядка. На рисунках 3.5 - 3.12 приведены все блоки в раскрытом виде. Так же на общую систему были нанесены 8 осциллографов «Scope», для того, чтобы в процессе изучения системы можно было наблюдать переходные процессы в разных точках системы. Также блок «Arrenius» для учета зависимости изменения коэффициента Аррениуса от температуры.
 |
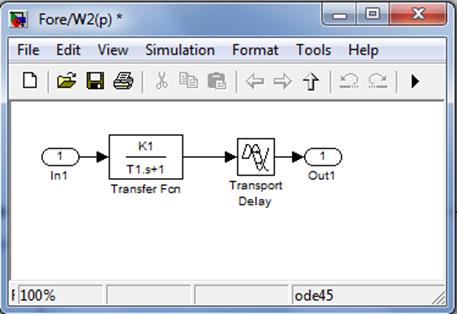Рисунок 3.4 - Общий вид математической модели в Simulink
Рисунок 3.5 - Блок передаточной функции выхлопной трубы W2(p)
Рисунок 3.6 - Блок передаточной функции измерительного устройства W3(p)
Рисунок 3.7 - Блок передаточной функции передающего устройства на автомобиле W4(p)
Рисунок 3.8 - Блок передаточной функции принимающего устройства в центре обработки ГЛОНАСС W5(p)
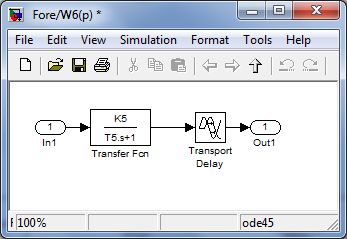
Рисунок 3.9 - Блок передаточной функции передающего устройства в центре обработки ГЛОНАСС W6(p)
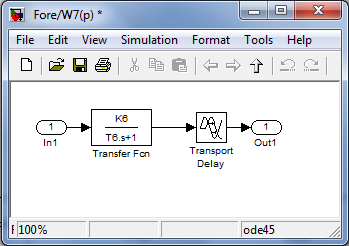
Рисунок 3.10 - Блок передаточной функции принимающего устройства на автомобиле W7(p)
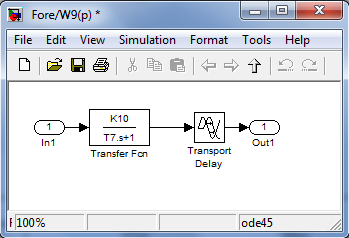
Рисунок 3.11 - Блок передаточной функции исполнительного устройства (нагреватель) W9(p)
Рисунок 3.12 - Блок передаточной функции катализатора W1(p)
Библиотека Simulink позволяет не собирать из отдельных элементов блок дискретного ПИД-регулятора, а воспользоваться уже готовым блоком «Discrete PID Controller». Его окно параметров представлено на рисунке 3.13. В этом окне мы имеем возможность менять, необходимые нам, параметры работы ПИД-регулятора:
- пропорциональный коэффициент k7(P);
- интегрирующий коэффициент k8(I);
- дифференцирующий коэффициент k9(D).
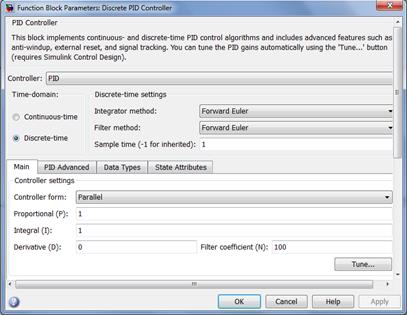
Рисунок 3.13 - Окно параметров блока «Discrete PID Controller»; передаточная функция Ws(p)
Введем в заготовленные блоки необходимые данные, они указаны в таблице 3.1. Коэффициенты k7, k8 и k9 (ПИД-регулятор) были получены в результате расчета по аналогии с [1].
Период дискретизации определяется по характеристикам контроллера h=0,00001 (с), остальные параметры приняты по справочной литературе [1].
Так расчет для выхлопной трубы производился, исходя из (объема газовой смеси 2,5 литра за оборот, длины выхлопной трубы составляет 2 м, удельного веса смеси 2,68 кг/нм3), а для катализатора предполагалось что соотношение веществ на поверхности платины практически не меняется, ≈ по 30%, и количество платины 2,1 гр.
Таблица 3.1 – Значения исходных параметров в отношении ед. и сек.
| Параметр | Значени | Параметр | Значение |
| x(t)/xmax | 1.0-0.1 | k4 | |
| А3 | 0.001454436 | T4, c | |
| τ1, c | 0.00000131 | τ4, c | 1-10(3) |
| T1, c | 1.5 | k5 | |
| k1 | T5,, c | 1-10 | |
| k2 | 0.8-0.9(0.8) | τ5, c | 1-10 |
| T2, c | 1-10(3) | k6 | |
| τ2, c | 1-10(2) | T6, c | |
| k3 | τ6, c | 1-10(2) | |
| T3, c | 1-10(5) | k10 | 0.91 |
| τ3, c | 1-10(7) | T7, c | 0.067 |
| τ7, c | 50 c |
На рисунках 3.14- 3.15 приведены изображения раскрытых блоков, после введения коэффициентов.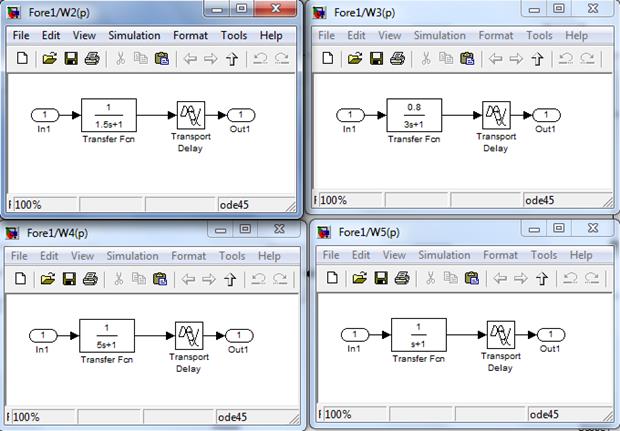 
Рисунок 3.14 - Блоки передаточных функций W2(p) – W5(p) с введенными исходными данными
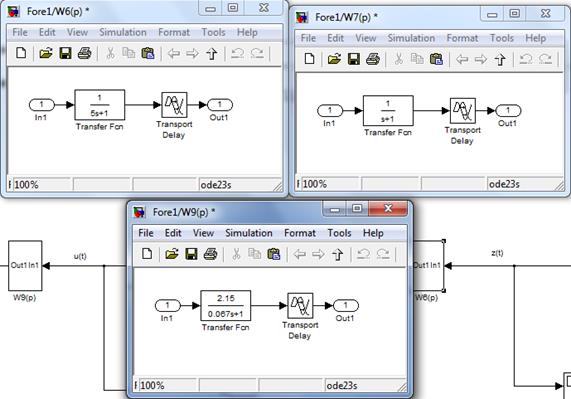
Рисунок 3.15- Блоки передаточных функций W6(p) W7(p) W9(p) с введенными исходными данными
Моделирование системы проводилось при следующих коэффициентах ПИД-регулятора: k7 =15, k8 = 1 и k9 = 0.15.
После вариации параметров ЗСУНВГА и коэффициентов ПИД-регулятора и анализа полученных результатов, в качестве настроек ПИД-регулятора выбираются коэффициенты приведенные в таблице 3.2.
Таблица 3.2 - Итоговые коэффициенты ПИД-регулятора
| Коэффициент | k7(P) | k8(I) | k9(D) |
| Значение | 0,5 | 0,15 |
Применения датчиков в автомобильной электронике разнообразны и ранжи- рованы от систем Powertrain и контро- ля эмиссии до систем безопасности и комфор- та. Группа датчиков положения/скорости/на- правления [1–8] на фоне прочих [7, 9–11] является наиболее многочисленной. Прежде чем перечислять общие требова- ния к автомобильным датчикам, следует от- метить, что самым общим и важнейшим тре- бованием к любым автомобильным устрой- ствам является достижение соотношения низкой цены и высоких объемов массового производства компонентов. Требования, предъявляемые к датчикам в отношении надежности, варьируются в за- висимости от принадлежности к автомо- бильной системе и расположения датчика (рис. 1). Они различаются для внутрикабин- ных датчиков (рис. 1а–в) — например, дат- чиков положения педали или угла поворо- та руля, и для датчиков, располагаемых под капотом или находящихся в непосредствен- ном контакте с окружающей средой (к ним относится датчик положения дроссельной заслонки, устанавливаемый с внешней сто- роны дроссельного корпуса на торце вала), и устройств, встраиваемых в коробку пере- дач или контролирующих работу двигателя или АБС. В зависимости от конкретного применения большинство автомобильных датчиков по- ложения используют обычную архитектуру, настраиваемую схемотехнически и конструк- тивно — с учетом типичных для данного применения специфических требований. К ним относятся: • способность работы при высоких темпе- ратурах (для большинства внешних дат- чиков положения стандартной рабочей температурой является –40…+125 °С; для встраиваемых систем рабочий темпе- ратурный диапазон регламентируется в пределах –40…+150 °С, с экстремальны- ми пределами воздействия рабочих темпе- ратур –50…150 °С и даже вплоть до 200 °С; для внутрикабинных датчиков рабочая температура может устанавливаться в пре- делах порядка –40…105 °C или даже — –30…85 °С); • функциональность с большими перепа- дами напряжения питания (в диапазоне порядка 2,7–5,5 В при номинальном пя- тивольтном питании, которое является стандартным для большинства датчиков положения, или порядка 7–15 В при пита- нии от 12-вольтного источника); • защита от напряжения питания обратной полярности (минимум той же величины, что и номинальное); • защита от короткого замыкания (КЗ) по цепи питания и выхода; • защита от перенапряжения (до 24 В, в за- висимости от времени воздействия); • сниженное энергопотребление (ток потреб- ления — 15–20 мА или менее); • устойчивость к электростатическому раз- рушению ESD (electrostatic discharge) — сверх 8 кВ или 250 пФ/1,5 кОм; • требования к электромагнитной совмес- тимости (ЭМС) и устойчивость к элект- ромагнитному излучению EMI (Electromagnetic Radiated Immunity) согласно ГОСТ 28751 — 90, DIN VDE 0870, DIN 40839, ISO 7637 (менее 1% или до 50 мВ смеще- ния напряжения питания в частотной по- лосе 1 МГц — 2 ГГц в электрическом по- ле 100–200 В/м). Электромагнитная совместимость — это способность электрического устройства ра- ботать удовлетворительно с электромаг- нитным окружением без недопустимого влияния (например, в соответствии с авто- ритетным для ИС Холла (рис. 2) немецким стандартом DIN VDE 0870). Стандарты не- мецкой национальной организации стан- дартов DIN 40839 и ISO 7637 гарантируют ЭМС для дорожных автомобилей и уста- навливают испытания: • DIN 40839-1: импульсные помехи по це- пям питания 12 В; • DIN 40839-2: импульсные помехи по це- пям питания 24 В; • DIN 40839-3: емкостные импульсы; • DIN 40839-3: излучаемые помехи. Существуют различные испытания для проверки воздействия на устройство элект- рического поля. Два наиболее обычных ме- тода, например для ИС Холла, включают: • измерения с сигнальным генератором эле- ктромагнитного поля частотой 10 кГц — 1 ГГц с электрическим полем до 250 В/м между двумя электродами, размещенны- ми на расстоянии примерно 1 м полоско- вой линии передачи. Компоненты не под- вергаются воздействию, только подключе- ние схемы, которое размещается в пределах указанного расстояния; • измерения в TEM (Transverse Electro Magnetic) камере — компоненты подвергаются воз- действию излучения частотой 100–750 кГц с напряженностью поля 100 В/м с 1 кГц АМ или 200 В/м без АМ. В России действует ГОСТ 28751-90 «Эле- ктрооборудование автомобилей. Электро- магнитная совместимость. Кондуктивные помехи по цепям питания. Требования и ме- тоды испытаний», который распространя- ется на вновь проектируемые электронные и электрические изделия, предназначенные для работы на автотранспортных средствах, и устанавливает требования к их электро- магнитной совместимости по кондуктив- ным помехам в бортовых сетях с номиналь- ным напряжением 12 и 24 В, а также мето- ды испытаний. На ГОСТ 28751-90 ссылается и ГОСТ 29157-91 «Совместимость технических средств элект- ромагнитная. Электрооборудование автомо- билей. Помехи в контрольных и сигнальных бортовых цепях. Требования и методы испы- таний». Он распространяется на электронные и электрические изделия, предназначенные для работы на автотранспортных средствах, проектируемые с 1993 года, и устанавливает требования к их электромагнитной совмес- тимости в части устойчивости к помехам от емкостных и индуктивных соединений в кон- трольных и сигнальных бортовых цепях с номинальным напряжением 12 и 24 В, а так- же методы испытаний. Другие стандарты, ка- сающиеся автомобильной ЭМС, названия которых перечисляются далее, включают ГОСТ 30378-95, ГОСТ 28279-89, ГОСТ 17822-91, а также ГОСТ 30601-97 «Совместимость тех- нических средств электромагнитная. Устрой- ства охранные сигнально-противоугонные автотранспортных средств. Требования и ме- тоды испытаний», ГОСТ Р 51856-2001 «Сов- местимость технических средств электромаг- нитная. Средства радиосвязи малого радиу- са действия, работающие на частотах от 3 кГц до 400 ГГц. Требования и методы испытаний» и ряд других, анализ необходимости учета которых может выясниться в процессе раз- работки автомобильных датчиков для новых применений. Самая общая информация по российским ГОСТам для автомобильных датчиков содер- жится в ГОСТ 3940. В 2004-м году широко известный ГОСТ 3940-84 «Электрооборудо- вание автотракторное. Общие технические условия», регламентирующий общие требо- вания к электрическим параметрам автомо- бильных датчиков, был заменен действую- щим поныне стандартом ГОСТ 3940-2004. На данный ГОСТ ссылаются ГОСТ 25651-83 «Приборы автомобилей контрольно-изме- рительные. Общие технические требова- ния. Методы испытаний», ГОСТ Р 50905-96 «Автотранспортные средства. Электронное оснащение. Общие технические требования», ГОСТ Р 50643-94 «Соединение разъемное для антиблокировочной системы тормозов. Основные размеры. Технические требования. Методы испытаний. Указания по установке на транспортных средствах». ГОСТ Р 50905-96 ссылается не только на ГОСТ 3940-2004, но и на многие другие важ ные для автомобильного конструктора-ме- хатроника ГОСТы: • ГОСТ 14254-96 «Степени защиты, обеспе- чиваемые оболочками (код IP)»; • ГОСТ 15150-69 «Машины, приборы и дру- гие технические изделия. Исполнения для различных климатических районов. Кате- гории, условия эксплуатации, хранения, транспортировки в части воздействия кли- матических факторов внешней среды»; • ГОСТ 17822-91 «Совместимость техничес- ких средств электромагнитная. Радиопо- мехи индустриальные от устройств с дви- гателями внутреннего сгорания. Нормы и методы испытаний»; • ГОСТ 23544-84 «Жгуты проводов для ав- тотракторного электрооборудования. Общие технические условия»; • ГОСТ 26003-80 «Система интерфейса для измерительных устройств с байт-последо- вательным, бит-параллельным обменом информацией. Требования к совместимо- сти»; • ГОСТ 27003-90 «Надежность в технике. Состав и общие правила задания требова- ний по надежности»; • ГОСТ 27435-87 «Внутренний шум авто- транспортных средств. Допустимые уров- ни и методы измерений»; • ГОСТ 27436-87 «Внешний шум автотранс- портных средств. Допустимые уровни и методы измерений»; • ГОСТ 28279-89 «Совместимость электро- магнитная электрооборудования автомо- биля и автомобильной бытовой радиоэле- ктронной аппаратуры. Нормы и методы измерений»; • ГОСТ 28751-90 «Электрооборудование ав- томобилей. Электромагнитная совмести- мость. Кондуктивные помехи по цепям питания. Требования и методы испыта- ний»; • ГОСТ 29157-91 «Совместимость техничес- ких средств электромагнитная. Электро- оборудование автомобилей. Помехи в кон- трольных и сигнальных бортовых цепях. Требования и методы испытаний»; • ГОСТ 30378-95 «Совместимость техничес- ких средств электромагнитная. Электро- оборудование автомобилей. Помехи от эле- ктростатических разрядов. Требования и методы испытаний». На документ ссылается параллельно дей- ствующий ГОСТ Р 52230-2004 «Электрообо- рудование автотракторное. Общие техниче- ские условия». Режим работы автомобиль- ных датчиков согласно этому ГОСТу — продолжительный S1. Классы нагрузки рег- ламентируются стандартом ГОСТ 25651-83 «Приборы автомобилей контрольно-изме- рительные. Общие технические требования. Методы испытаний». Требования к конструкции датчика вклю- чают: • высокую степень защиты датчика от попа- дания внутрь твердых тел и воды вплоть до IP67, IP68 или IP69 (согласно междуна- родной классификации и в соответствии с ГОСТ 14254-96); • устойчивость к влажности, загрязнениям, агрессивным средам (включая воду, росу, иней, туман, соляной туман, масло, бензин и различные виды топлива, антифриз, ав- тошампуни, аккумуляторную кислоту, тор- мозную жидкость); • ударопрочность — устойчивость к удар- ным нагрузкам порядка 100 g и длительно- стью удара до 11 мс; • вибропрочность — устойчивость к случай- ным гармоническим колебаниям с часто- той 20–2000 Гц и эффективным значени- ем ускорения до 20 g по каждой из трех осей; • требования к надежности по ГОСТ 27003-90 (датчики относятся к изделиям конкрет- ного назначения (ИКН) вида I, невосста- навливаемым, неремонтируемым и необ- служиваемым ИКН непрерывного дли- тельного или многократного циклического применения; средняя наработка на отказ — не менее 3000 часов, что соответствует про- бегу автомобиля 150 000 км в течение 10 лет; сроки гарантийных периодов — не менее 3 лет (до десяти лет), долговеч- ность — 10 лет). Рекомендуемый момент крепления болта при монтаже датчика составляет 1,60–2,2 Н·м (в некоторых устройствах может быть до 8 Н·м). Многие аналоговые или переключаемые датчики подключаются к автомобильной си- стеме (такой как Engine Control Unit (ECU)) посредством трехпроводного соединителя (например, P2S Metri-Pack серии 150 Packard Electric или 444043-1 AMP). Это соединение обеспечивает подключение «плюса» питания, «земляного» фрейма и возможность снятия сигнала, например, аналогового пропорци- онального сигнала положения или цифро- вого импульсного (частотного) сигнала ско- рости. Регламентируемое сопротивление изо- ляции штыревых контактов — порядка 10 МОм. Механическая прочность штыре- вых контактов должна быть не менее 58,8 Н, нагрузка при извлечении штекера — не бо- лее 44,2 Н. Система, получающая и обрабатывающая сигнал датчика положения, обычно включа- ет микроконтроллер, при этом получение аналогового сигнала производится через од- ноканальный вход АЦП. В автомобильную систему часто входит и так называемый pullup резистор в сигнальной цепи, в связи с чем формируются требования к номиналу рези- стивной нагрузки (не менее 7,5 кОм или не менее 250 кОм) или суммарной емкости на- грузки (не более 15 пФ). Двухпроводные ШИМ-датчики переда- ют выходной сигнал модуляцией общего тока потребления датчика. В контрольном блоке в цепь питания датчика последова- тельно включен резистор. Падение напря- жения на этом резисторе отслеживает ком- паратор, с выхода которого снимается сиг- нал датчика. Более сложные интерфейсы строятся по тем же принципам, но используют большее число выводов контактного или проводного соединителя. Расширенные схемотехнические требова- ния включают требования к точности (по- рядка 0,5%, не менее 1%), быстродействию датчика, малого времени после включения power-on или power-up, линейности аналого- вой выходной характеристики или времени нарастания/спада фронта импульса. Высокие температуры часто требуют при- менения EEPROM в схеме обработки сигна- ла датчика. В EEPROM во время калибровки программируются и запасаются корректиру- ющие коэффициенты, используемые схемой ЦОС для корректировки смещения, чувстви- тельности, нелинейности и других факто- ров — например, температурного коэффи- циента магнита. К ИС датчиков, работающим в жестких условиях эксплуатации, предъявляется тре- бование соответствия квалификационному стандарту Automobile Electronics Council (AEC Q100). Многие новые датчики являются RoHS (Restriction of Hazardous Substances) совмес- тимыми. Помимо того, автомобильные датчики должны выдерживать испытания на воздей- ствие следующих факторов: • термоциклирования (например, порядка 24–100 циклов изменения температуры от –40 °C до 100–120 °C в течение 48 часов или 500 циклов изменения температур от –40 до 150 °C), • холодоустойчивости (к работе при темпе- ратуре –40 °C в течение не менее 100 часов, • теплоустойчивости — например, к работе при температуре +105 °C в течение не ме- нее суток или в течение 144 часов при тем- пературе +150 °C, • влагоустойчивости — к работе при воздей- ствии влажной среды с относительной влажностью 85% при температуре +80 °C в течение не менее 5 суток, с относительной влажностью 98% — до 120 часов на 38 °C, • коррозионной стойкости (сохранение ра- ботоспособности при воздействии 5%-но- го соляного тумана при температуре 38 °C в течение 96 часов согласно ГОСТ 9308-85), • испытаний на погружение устройства в во- ду (ее температура равна 25 °C) в течение 5 мин (контроль утечки), • устойчивости к воздействию топливных паров (15% метанола, 15% этанола и индо- ла Indolene HO в течение 48 часов для каж- дого вида), • устойчивости к воздействию озона 100 ppm при температуре 38 °C в течение 72 часов, • устойчивости к воздействию пыли ско- ростью 48 км/ч при температуре 80 °C в течение 9 часов или с концентрацией 0,003–0,014 г/см3 в течение 9 часов или в пылевой камере 1 м3. Приведенные данные взяты из типичных автомобильных спецификаций датчиков раз- личных производителей — для того чтобы отразить общий уровень исполнений авто- мобильных измерительных устройств. В России по устойчивости к воздействию внешних климатических факторов автомо- бильные датчики должны соответствовать климатическому исполнению изделий соглас- но ГОСТ 15150-69. Этот же стандарт регла- ментирует условия транспортировки и хра- нения в части воздействия климатических факторов. Зарубежные международные, региональ- ные и национальные стандарты, а также стан- дарты автомобильных объединений и кон- сорциумов, регламентирующие испытания для автомобильных датчиков положения и скорости, включают стандарты (примеры даны в скобках): • Ассоциации автомобильных инженеров SAE (Society of Automotive Engineers) (SAE J726 для устойчивости к пыли); • Японской ассоциации стандартов (Japanese Standards Association) JIS (Japanese Industrial Standards) (JIS D0203 для водоустойчивос- ти, JIS D0207-F2 для чувствительности к пыли); • Американского общества по испытанию материалов ASTM (American Society of Testing Materials) (ASTM-B117 для корро- зионной стойкости); • Международной электротехнической комис- сии (МЭК) — International Electrotechnical Commission (IEC) (IEC 68-2-30 — испыта- ния на влагостойкость, IEC 68-2-11 — испы- тания на воздействие соляного тумана); • Немецкой национальной организации DIN (DIN 40050 — испытания на влагостой- кость орошением направленной струей под давлением, DIN 40839 — испытания на эле- ктромагнитную совместимость); • Ассоциации электронной промышленно- сти EIA (Electronic Industries Association или Electronic Industries Alliance) и входящим в ее состав инженерным органом стандар- тизации полупроводниковых технологий Solid State Technology Association JEDEC Joint Electron Device Engineering Council, оп- ределяющими действующие электронные стандарты в США (EIA/JESD22-A114-B, JESD22-A114C.01, JESD22-A114D) HBM (Human Body Model) для защиты от элек- тростатического разрушения); • военные стандарты, утверждаемые Мини- стерством обороны США (Department of Defense) (включая военные стандарты MIL STD 883D по ESD, MIL-STD 883E — устойчивость к ударам до 500 g) • и другие. Таким образом, в мире существует доста- точно много стандартов для автомобильных устройств, как глобального или отраслево- го, так и национального масштаба, причем игнорировать последние нельзя — ввиду опасности маркетинговых неудач в данной стране. Для обеспечения надежности автомобилей важнейшее значение имеет повышение каче- ства различных автомобильных компонен- тов (уменьшение числа дефектных изделий в ppm — parts per million). По статистике АвтоВАЗа, 70–75% дефектов автомобилей связано с дефектами автокомпонентов, что не только негативно воздействует на имидж автомобилей, но и приводит к экономичес- кому ущербу для их производителей и дис- трибьюторов. Существуют стандарты выборки DIN 40080 (содержание соответствует MIL-STD 105 D и IEC 410). Инструкции этих стандартов та- ковы, что вероятность принятия поставлен- ной партии выше 90%, если процентное со- отношение дефектов не превышает уровень AQL (AQL — Acceptable Quality Level). Европейские автомобильные стандарты ка- чества, как видно, отличаются разнообразием и прежде даже создавали трудности для спе- циалистов компаний, стремящихся продавать свои автомобили на европейском рынке. Основные автомобильные европейские стандарты качества, которые необходимо учитывать специалисту, включают AVSQ (Association of Quality System Evaluators) (Ита- лия), EAQF (аббревиатура расшифровывает- ся для англоязычных читателей как evaluation, aptitude, quality and supplier) (Франция) и VDA 6.1 (Verband der Automobilindustrie) (Германия). В США действует автомобиль- ный стандарт QS-9000, он определяющий для международной рабочей группы International Automotive Sector Group (IASG), в которую входят автомобильные представители OEM, органы аккредитации, регистраторы и по- ставщики. Но на автомобильные датчики распрост- раняется тенденция объединения и перехода от разнообразных национальных, региональ- ных и прочих стандартов, включая ГОСТы, к международному стандарту качества, ко- торым является международный отрасле- вой стандарт ISO/TS 16949:2002 (ИСО/ТУ 16949:2002), разработанный для автомо- бильной промышленности на основе стан- дартов ИСО 9000, ISO 9000/1. Как известно, организации ISO (International Organization for Standardization, Международ- ная организация по стандартизации) и IEC (МЭК) признаны всеми странами и имеют полномочия издавать международные стан- дарты, распространяющиеся на автомобиль- ные датчики, называемые также стандарта- ми де-юре или формальными стандартами