Задача №1. Равновесие плоской системы сил
Жесткая рама закреплена в точке А шарнирно, а в точке В прикреплена к шарнирной опоре на катках; стержень прикреплен к раме и к неподвижной опоре шарнирами.
На раму действуют пара сил с моментом М = 100 Н·м и две силы.
Требуется определить реакции связей в точках А и В, вызываемые заданными нагрузками. При окончательных подсчетах принять 
м.
Дано:
М = 100 Н·м; F1=10 H; F2=40 H
α = 30°; β = 60°; м
Аналитическое решение:
Из условия, что тело находится в равновесии, следует следующая система уравнений:
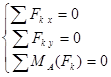
Для данной задачи исходя из системы составим соответствующие уравнения:
Из (1) найдем 
:
Из (3) найдем 
:
Из (2) подставив , найдем 
:
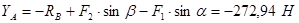
Знак "-" указывает на противоположное направление силы, чем было выбрано, т. е. силы будут направлены так:
Ответ: 
Проверка:
Составим момент сил относительно точки В:
Задача №2. Равновесие пространственной системы сил
Однородная прямоугольная плита весом Р = 5 кН со сторонами АВ = 3 l, ВС = 2 l закреплена В точке А сферическим шарниром, а в точке В цилиндрическим шарниром (подшипником) и удерживается в равновесии невесомым стержнем СС’. На плиту действует пара сил с моментом М = 6 кН·м, лежащая в плоскости плиты, и две силы: 
лежащая в плоскости, параллельной плоскости xz и сила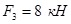 
- в плоскости, параллельной плоскости yz. Точки приложения сил (E,D) находятся в серединах сторон плиты.
Требуется определить реакции связей в точках А, В, С.
При окончательных подсчетах принять l = 0,8 м.
Дано:
Р = 5 кН; М = 6 кН·м; F2=6 кH; F3=8 кH
F2 ┴ Oz; α = 30°; АВ= 
; ВC= 
; 
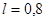м
Аналитическое решение:
Из условия, что тело находится в равновесии, следует следующая система уравнений:
Для данной задачи получим следующую систему уравнений:
Ответ: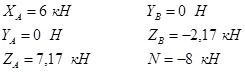 
Знак "-" указывает на противоположное направление силы, чем было выбрано.
Задача №3. Кинематика точки
Точка В движется в плоскости xy. Закон движения точки задан уравнениями: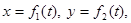 
где x и y выражены в сантиметрах, а t - в секундах.
Найти уравнение траектории точки; для момента времени t=1 c определить скорость и ускорение точки, а также касательное и нормальное ускорение и радиус кривизны в соответствующей точке траектории. Вычертить в масштабе траекторию точки, показать ее начальное положение и положение в заданный момент времени, показать на рисунке полные скорость и ускорение точки, их проекции на координатные оси, касательное и нормальное ускорение точки.
равновесие траектория скорость кривизна
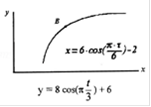
Дано:
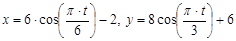
Аналитическое решение:
Так как уравнения заданы в параметрической форме, тогда для перевода этих уравнений к каноническому виду воспользуемся тригонометрическим тождеством о двойном угле: 
Значит
Отсюда, приравняв левые части уравнений, получим следующий вид канонического уравнения движения материальной точки:
- уравнение параболы
В момент времени 
материальная точка имела положение 
, а в момент времени 
- в положении 
Определим скорость движения материальной точки через проекции на координатные оси:
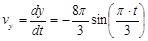
Результирующая же скорость будет равна 
Тогда в момент времени 
, получим следующие величины проекций и результирующей скорости:
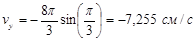
Аналогично скорости определим ускорение материальной точки:
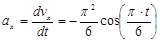
Результирующая же скорость будет равна
Тогда в момент времени 
, получим следующие величины проекций и результирующего ускорения:
Для определения касательного ускорения продифференцируем следующее равенство:
Отсюда следует, что 
, тогда в момент времени 
Так как 
, то нормальное ускорение найдем по следующей формуле:
Радиус кривизны определим учитываю, что
