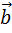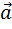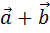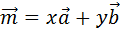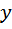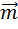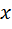Если на некотором отрезке задано начало отрезка и его конец, о такой отрезок называется направленным. В векторной алгебре направленный отрезок называется вектором.
Геометрически вектор изображается в виде отрезка со стрелкой и обозначается 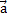 или
или 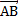 .
.
Нулевым вектором называется вектор, начало и конец которого совпадают. Длиной (модулем) вектора называется длина порождающего его отрезка.
Длина отрезка, изображающего вектор, называется длиной вектора, модулем или абсолютной величиной.
Модуль любого не нулевого вектора выражается положительным числом и обозначается 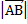 .
.
Два вектора называются равными, если они имеют одинаковые модули и одинаковые направления.
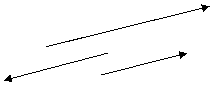 Два вектора
Два вектора 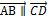 называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные векторы называют сонаправленными и пишут
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные векторы называют сонаправленными и пишут 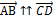 , если их направления совпадают и противоположно направленными
, если их направления совпадают и противоположно направленными 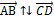 , если направления векторов противоположно направлены.
, если направления векторов противоположно направлены.
Два коллинеарных вектора называют равными, если они сонаправлены и имеют равные длины.
В пространстве имеет место понятии компланарности векторов.
Три и большее число ненулевых векторов в пространстве называются компланарными, если они лежат на прямых, параллельных одной плоскости.
Любой вектор равен самому себе. Если два вектора по отдельности равны третьему, то они равны между собой.
Вектор, модуль которого равен 1, называется единичным вектором.
Ортом данного вектора называется вектор, который направлен одинаково с данным вектором и имеет модуль равный 1. Обозначается а0. 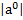 =1
=1
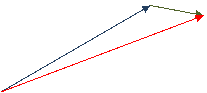
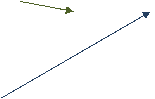
Суммой векторов  и
и  называется такой вектор
называется такой вектор  , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  , а конец - с концом вектора
, а конец - с концом вектора  , при условии, что начало вектора
, при условии, что начало вектора  перенесено в конец вектора
перенесено в конец вектора  .
.
|
|
|
 | |||
 | |||
|
|
|
|
Разностью векторов 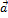 и
и  называют сумму вектора
называют сумму вектора 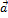 и
и 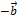 .
.
Свойства суммы векторов:
ü переместительный закон a+b=b+a
ü сочетательный закон (a+b)+c=a+(b+c)
ü a+0=a
Произведением вектора 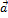 на действительное число k называется вектор k
на действительное число k называется вектор k 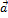 , который имеет длину, равную k
, который имеет длину, равную k 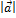 ,и коллинеарен
,и коллинеарен 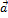 . При этом если k>0, то векторы
. При этом если k>0, то векторы 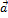 и k
и k 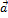 сонаправлены, если k<0, то векторы
сонаправлены, если k<0, то векторы 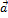 и k
и k 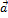 противоположно направлены.
противоположно направлены.
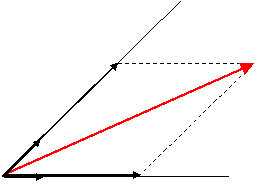
Линейной комбинацией векторов a1, a2, a3,... an называется сумма произведений этих векторов на какие-либо числа k1, k2, k3,... kn. Любой вектор m на плоскости может быть представлен единственным способом в виде линейной комбинации двух неколлинеарных векторов.
 |
|
|
|
|
|
|
|
Говорят, что вектор 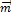 разложен в базисе
разложен в базисе 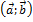 .
.
Базисом на плоскости называется пара неколлинеарных векторов, взятых в определенном порядке. Числа x и y называются координатами вектора 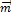 в базисе
в базисе 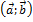 .
.
В пространстве это будет выглядеть так:
Если три вектора а, в, с, попарно неколлинеаерны и некомпланарны, тот любой вектор пространства может быть единственным образом разложен по этим векторам, т.е. может быть представлен в виде r=xa+yb+zc, где a, b, c – некоторые числа.
Прямоугольная система координат в пространстве определяется заданием масштабного отрезка и трех попарно перпендикулярных осей.
Единичные векторы i, j, kназывают ортами координатных осей.
X – абсцисса
Y - ордината
Z - аппликата
1. Запишите разложение векторов по координатным векторам i, j, k
|
|
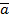 (2;3;-5)=2i+3j-5k;
(2;3;-5)=2i+3j-5k; 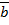 (5;0;7)=5i+7k
(5;0;7)=5i+7k
2. Запишите координаты векторов
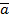 =5i+2j+6k=
=5i+2j+6k= 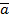 (5;2;6);
(5;2;6); 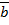 =8i+9k=
=8i+9k= 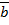 (8;0;9)
(8;0;9)
Для нахождения координат вектора нужно из координат его конца вычесть координаты начала:
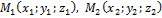 ;
;
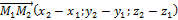 .
.
Действия над координатами, заданными своими координатами:
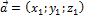 ;
; 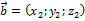
1) при сложении двух и большего числа векторов их одноименные координаты складываются
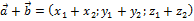 ;
;
2) при вычитании векторов их одноименные координаты вычитаются
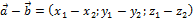 ;
;
3)при умножении вектора на число каждая координата вектора умножается на это число
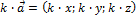 .
.
Длина вектора вычисляется по формуле
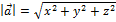 ;
;
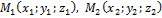 ;
;
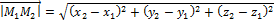 .
.
Задача: Выполнить действия, если А(-2;5;-1), В(-1;-1;6), С(-1;0;2), D(0;-5;-1):
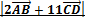 ;
;
Решение:
Найдем координаты векторов:
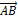 =
= 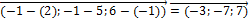 ;
;
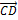 =
= 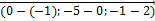 =
= 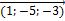 ;
;
2  =2
=2 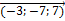 =
= 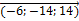 ;
;
11 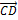 =11
=11 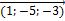 =
= 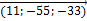 ;
;
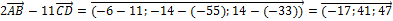 ).
).
Вычислим длину вектора 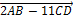 :
:
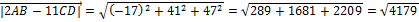 .
.
Ответ: 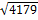 .
.
Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними:
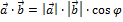
Скалярное произведение векторов, заданных своими координатами, рано сумме произведений одноименных координат:
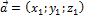 ;
; 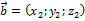
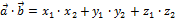 .
.
Скалярное произведение двух векторов обладает следующими свойствами:
1. коммутативность а*в=в*а
2. а*(в+с)=а*в+а*с
3. 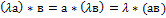
Скалярное произведение вектора само на себя называется скалярным квадратом.
Задача:Выполнить действия, если 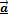 (1;1;0),
(1;1;0), 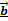 (-1;-2;1),
(-1;-2;1), 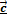 (1;1;1):
(1;1;1):
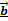 (8
(8 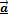 +13
+13 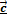 ).
).
Решение:
Найдем координаты векторов:
8 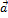 =8
=8 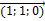 =(
=( 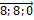 ); 13
); 13  =13
=13 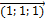 =(
=( 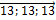 ).
).
8 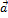 +13
+13 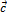 =(
=( 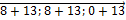 )=(
)=( 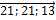 ).
).
Найдем скалярное произведение векторов:
 (8
(8 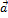 +13
+13 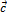 )=
)= 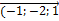 )∙ (
)∙ ( 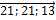 )=-1∙21+(-2)∙21+1∙13=-21-42+13=-50.
)=-1∙21+(-2)∙21+1∙13=-21-42+13=-50.
Ответ: -50.
Углом между двумя векторами 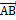 и
и 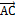 называется меньший из ориентированных углов между направленными отрезками
называется меньший из ориентированных углов между направленными отрезками 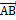 и
и 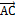 , исходящими из одной точки.
, исходящими из одной точки.
|
|
Угол между векторами можно найти по формуле
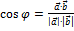 .
.
Задача: В треугольнике, заданном вершинами А(-1;1;1), B(1;0;-1), С(1;1;1):
|
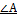 , АВ, СВ.
, АВ, СВ.
Решение:
|
|
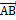 =(
=( 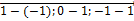 )=(
)=(  );
);
 -(
-( 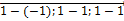 )=(
)=( 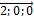 );
);
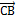 =(
=( 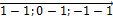 )=(
)=( 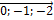 ).
).
Найдем длины векторов:
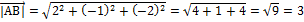 ;
;
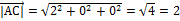 ;
;
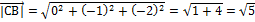 .
.
Найдем скалярное произведение векторов:
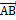 ∙
∙ 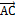 =(
=(  )∙(
)∙( 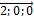 )=2∙2+(-1)∙0+(-2)∙0=4+0+0=4.
)=2∙2+(-1)∙0+(-2)∙0=4+0+0=4.
Найдем косинус угла А:
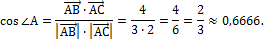
По таблице Брадиса найдем угол: 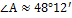 .
.
Ответ: 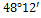 ; 3;
; 3; 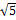 .
.