Коды с обнаружением ошибок
Методы помехозащищенного кодирования направленные только на обнаружение ошибки называют – коды обнаружения ошибок. Обнаружение ошибки позволяет, в некоторых ситуациях, перезапросить данные с источника и исправить ошибку. Ну или не использовать ошибочные данные. Поскольку коррекция ошибок в этих методах не требуется, то размер дополнительно передаваемой информации минимален.
Простейшим кодом обнаружения ошибок является «контроль четности».
Код с проверкой на четность
Проверка четности – очень простой метод для обнаружения ошибок в передаваемом пакете данных.
Всё сообщение разбивается на блоки бит равного размера, например, по 8-мь бит. И вычисляется сумма значений бит каждого из этих блоков. К блоку добавляется еще один бит: если сумма нечетная, то бит 1, иначе — бит 0. Т.е. получается блок длиной на один бит больше исходного — это «бит четности», так называемый, паритетный бит. Этот бит устанавливается во время записи (или отправки) данных, и затем рассчитывается и сравнивается во время чтения (получения) данных. Он равен сумме по модулю 2 всех бит данных в пакете. То есть число единиц в пакете всегда будет четно. Изменение этого бита (например с 0 на 1) сообщает о возникшей ошибке.
При получении данных вычисление «бита четности» повторяется и результат сравнивается с переданным битом четности. Если вычисленное и переданное значение «бита четности» совпадают, значит ошибки не было, иначе — ошибка.
С помощью данного кода мы не можем восстановить данные, но можем обнаружить только лишь одиночную ошибку. Такой код образуется путем добавления к передаваемой комбинации, состоящей из k информационных символов, одного контрольного символа (0 или 1), так, чтобы общее число единиц в передаваемой комбинации было четным.
Легко сообразить, что искажение двух, четырех и любого четного количества бит в блоке не будет обнаружено.
Пример:
Начальные данные: 1111
Данные после кодирования: 1111 0 (1 + 1 + 1 + 1 = 0 (mod 2))
Принятые данные: 1 0 110 (изменился второй бит)
Как мы видим, количество единиц в принятом пакете нечетно, следовательно, при передаче произошла ошибка.
Как говорилось ранее, этот метод служит только для определения одиночной ошибки. В случае изменения состояния двух битов, возможна ситуация, когда вычисление контрольного бита совпадет с записанным. В этом случае система не определит ошибку, а это не есть хорошо.
К примеру:
Начальные данные: 1111
Данные после кодирования: 1111 0 (1 + 1 + 1 + 1 = 0 (mod 2))
Принятые данные: 1 00 10 (изменились 2 и 3 биты)
В принятых данных число единиц четно, и, следовательно, декодер не обнаружит ошибку.
Так как около 90% всех нерегулярных ошибок происходит именно с одиночным разрядом, проверки четности бывает достаточно для большинства ситуаций.
Решите задачу 1:
Закодируйте слово длины 4 с помощью кода с проверкой четности.
| а) α =(0011) | б) α =(1011) | в) α =(0111) | г) α =(0001) | д) α =(0010) |
| е) α =(1010) | ж) α =(0110) | з) α =(1001) | и) α =(1000) | к) α =(1100) |
Образец: Закодируйте слово α =(0101) длины 4 с помощью кода с проверкой четности.
Решение: Найдем сумму по модулю 2 всех двоичных букв этого слова. Имеем:
 , поэтому передано будет сообщение в виде слова b =(01010) длины 5.
, поэтому передано будет сообщение в виде слова b =(01010) длины 5.
Решите задачу 2:
Декодируйте слово длины 5 с помощью кода с проверкой четности
| а) b =(00110) | б) b =(10111) | в) b =(01110) | г) b =(00011) | д) b =(00101) |
| е) b =(10100) | ж) b =(01100) | з) b =(10010) | и) b =(10001) | к) b =(11001) |
Образец: Декодируйте слово b =(01110) длины 5 с помощью кода с проверкой четности.
Решение: Отбросив последнюю букву передаваемого слова, имеем слово α =(0101) длины 4, которое передавалось по каналу связи.
Решите задачу 3:
Определите, допущены ли ошибки в сообщении, заданном в задании 2.
Образец: Определите, допущены ли ошибки в сообщениях a 1=(01110) и a 2= (01010).
Решение: Для обнаружения ошибки, проверим с помощью М2 сумму всех букв закодированного слова в полученных сообщениях: a 1=  . Т.к. сумма всех букв закодированного слова оказалась равной 1, то при его передаче по каналу связи была допущена ошибка.
. Т.к. сумма всех букв закодированного слова оказалась равной 1, то при его передаче по каналу связи была допущена ошибка.
Для второго сообщения имеем a 1= 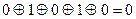 . Т.к. сумма всех букв закодированного слова оказалась равной 0, то при его передаче по каналу связи код с проверкой четности не позволяет выявить ошибку.
. Т.к. сумма всех букв закодированного слова оказалась равной 0, то при его передаче по каналу связи код с проверкой четности не позволяет выявить ошибку.
1.2 Код «циклическая сумма»
Другим примером кодов обнаружения ошибок является «циклическая сумма » (Cyclic Redundancy Checksum или CRC). Этот метод является неблочным, но может быть использован и в блочном варианте. Принцип обнаружения ошибки схож с кодом «контроля четности». Используя особый алгоритм суммируются значения всех битов данных или порции данных, в результате суммирования получается некое число (не один бит, а несколько), которое передается вместе с данными или порцией данных. Принимающая сторона вычисляет CRC повторно и сравнивает с переданным.
«Контроль четности» — частный случай CRC.
1.2. Код с постоянным весом ( блочный неразделимый)
В теории кодирования весом кодовых комбинаций принято называть количество единиц, которое они содержат. Если все комбинации кода имеют одинаковый вес, то такой код называется кодом с постоянным весом. Коды с постоянным весом относятся к классу блочных неразделимых кодов, так как здесь не представляется возможным выделить информационные и контрольные символы. Из кодов этого типа наибольшее распространение получил обнаруживающий семизначный код 3/4, каждая разрешенная комбинация которого имеет три единицы и четыре нуля. Известен также код 2/5. Примером комбинаций кода 3/4 могут служить следующие семизначные последовательности: 1011000, 0101010, 0001110 и т. д.
Декодирование принятых комбинаций сводится к определению их веса. Если он отличается от заданного, то комбинация принята с ошибкой. Этот код позволяет обнаруживать любые одиночные ошибки и часть многократных ошибок. Не обнаруживаются только так называемые ошибки смещения, сохраняющие неизменным вес комбинации, когда одновременно одна единица переходит в ноль и один ноль переходит в единицу, два ноля и две единицы меняются на обратные символы и т.д. Ошибки смещения характеризуются тем, что число искаженных единиц всегда равно числу искаженных нулей.
Примером кода с постоянным весом является Международный телеграфный код МТК-3. В этом коде все разрешенные кодовые комбинации имеют вес равный трем, разрядность же комбинаций n=7. Таким образом, из 128 комбинаций (N0 = 27 = 128) разрешенными являются Nа = 35 (именно столько комбинаций из всех имеют W=3). При декодировании кодовых комбинаций осуществляется вычисление веса кодовой комбинации и если W<>3, то выносится решение об ошибке. Например, из принятых комбинаций 0110010, 1010010, 1000111 ошибочной является третья, т. к. W=4.
С37= n! / (n-m)!*m! =35
Рассмотрим код с тремя единицами из семи. Для этого кода возможны смещения трех типов.

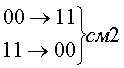

Например, код  при
при  коэффициент обнаружения составит
коэффициент обнаружения составит  , избыточность L=27%.
, избыточность L=27%.
Пример. Коды с двумя единицами из пяти и тремя единицами из семи.

| 
|
Код Грея
Для уменьшения вероятности ошибки в двоичных кодах используют код Грея, в котором каждые две позиции отличаются только одним разрядом, т.е. на 1 бит. Поэтому выходной сигнал может быть представлен лишь одним из двух состояний: истинный или ложный. Код Грея тоже использует лишь два знака 0 и 1, но соседние числа отличаются только в одном разряде, т.е. на 1 бит информации.