Построить график и указать точку на нем. Пояснить метод решения задачи.

 

 

 

 

№ 2

Простые числа. Сформировать с помощью функции RND массив из 120 элементов. Найти все простые числа. Построить график и нанести их на числовую ось в любом масштабе в пределах экрана. Пояснить метод решения задачи..

 

 

№ 3

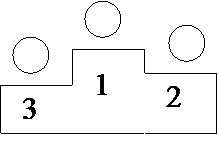
Обработка результатов соревнований. В ЭВМ поступают результаты соревнований по плаванию для трех спортсменов. Выбрать и напечатать лучший результат. Решить задачу для следующих наборов данных: 1) 11,3; 10,6; 11; 2) 10; 10,9; 13; 3) 16; 18; 13.

Создать программу с диалогом: «введите три тройки результатов (*,*,*),(*,*,*), (*,*,*).

Вывести результаты решения в графической и символьной форме.

 

№4

Календарь. Определить порядковый номер дня по заданной дате

Ограничения: високосные годы это те, у которых число делится на

400 и 4, но не делится на 100. Пояснить метод решения задачи..

№ 5

 

Совмещение геометрических фигур. Даны площадь круга R и квадрата S. Определить, поместиться ли квадрат в круге. Задачу решить при 1) R = 70, S = 36,74; 2) R = 0,86, S = 0,64. 3) R = 6, S = 9.

Определить, поместиться ли круг в квадрате. Задачу решить при: 1) R = 3,2, S = 3,5; 2) R = 3,2, S = 4; 3) R = 6, S = 9. Пояснить метод решения задачи.

 

№ 6

 

Равные элементы. Сгенерировать функцией RND 2 массива по 20 элементов. Упорядочить каждый массив по возрастанию. Написать номера (№ №) и значение равных элементов. Если нет, то написать комментарий «Равных элементов нет». Нанести массив на числовую ось в масштабе в пределах экрана и цветом выделить N _J1 =N_J2, создать в программе обе ситуации. Пояснить метод решения задачи.

 

 

№ 7

Определить, принадлежит ли точка D треугольнику ABC. (Треугольник задан координатами своих вершин.) Решить задачу при A (2;2), B (4;5), C (7;3) и 1) D (4;3); 2) D (6;4,5); 3) D (3;4).

Создать программу с диалогом: «введите координаты точки»

Вывести в графической и текстовой форме. Пояснить метод решения задачи.

 

 

№ 8

Вычисление значений функции. Организовать вывод массива результатов расчета значений функции в табличный файл и построить график (в декартовых координатах с цифрами по осям) этой функции на экране в интервале [-1;1]

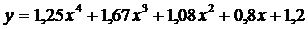в интервале 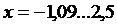с шагом 0,05. Пояснить метод решения задачи.

 

 

№ 9

 

Принадлежность точки окружности. Заданы координаты двух точек. Определить, лежат ли они на одной окружности с центром в начале координат. Результат присвоить символьной переменной. Задачу решить для точек с координатами (0; 2), (2; 0), (1; 3), (2; 2).

Создать программу с диалогом: «введите координаты двух точек М1 и М2». Результаты вывести в графической и текстовой форме. Пояснить метод решения задачи.

№ 10

 

Питание школьников. Учащимся в 1 классе назначено дополнительное питание 1 стакан (200 мл.) молока, если вес учащегося менее 30 кг. Составить список 25 учащихся, указать их вес и определить, сколько пакетов по 1л молока надо привозить в буфет школы дополнительно. Построить диаграмму и вывести исходный список учащихся. Пояснить метод решения задачи.

 

 

№ 11

 

Обработка результатов соревнований. В ЭВМ по очереди поступают результаты соревнований по плаванию, в которых участвуют n спортсменов. Выдавать на печать лучший результат после ввода результата очередного спортсмена. Результаты выводить в виде накопительной таблице. Алгоритм построить в диалоговом режиме. Пояснить метод решения задачи.

№ 12

Книжный магазин. В продаже книг в книжном магазине принимает участие ЭВМ. Составить программу, которая запрашивает стоимость книг, сумму денег, внесенную покупателем, а далее определяет причитающуюся сдачу (если денег внесено больше), печатает «спасибо», если сдачи не требуется, или выдает сообщение о недостаточности, внесенной суммы. Исходные данные вводить самостоятельно в диалоговом режиме. Результаты выводить в пополняющейся таблице. Пояснить метод решения задачи.

 

№ 13

Пирамида из N шаров. Представим себе пирамиду из N шаров. Следующий слой состоит из N-1 шаров и т. д. Верхний слой содержит 1 шар. Требуется определить, сколько шаров потребуется для строительства пирамиды из M слоев.

Вывод в графической и текстовой форме. Пояснить метод решения задачи.

 

№ 14

Успеваемость. Вводя в цикле по 5 оценок каждого студента, подсчитать число студентов, не имеющих оценок 2 и 3. В группе учится n студентов.

Вводя в цикле по 4 оценки, полученные студентами в сессию, определить число неуспевающих студентов и средний бал группы по всем экзаменам. Пояснить метод решения задачи.

 

 

№ 15

Вычислить площадь фигуры. Вычислить площадь заштрихованной части фигуры, где x меняется от 0 до p/2.

 

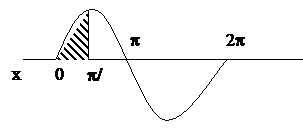Вывести на печать входные данные и результат. Пояснить метод решения задачи.

 

 

 

№ 16

Точка на окружности. На плоскости расположена окружность радиуса R с центром в начале координат. Ввести заданные координаты точки и определить, лежит ли она на окружности. Результат присвоить символьной переменной. Решить задачу при R =2 для точек с координатами (0; 2), (-1,5; 0,7), (1; 1), (3; 0). Пояснить метод решения задачи

 

 

№ 17

Определение подходящего возраста. Составить программу для определения подходящего возраста кандидатуры для вступления в брак, используя следующее соображение: возраст девушки равен половине возраста мужчины плюс 7, возраст мужчины определяется соответственно, как удвоенный возраст девушки минус 14. Данные для проверки работы программы задать самостоятельно. Пояснить метод решения задачи.

 

№ 18

Задано n троек чисел a, b, с. Вводя их по очереди и интерпретируя как длины сторон треугольника, определить сколько троек может быть использовано для построения треугольника (числа a, b, с при вводе расположить в порядке возрастания: a £ b £ с). Результат вывести графически ив форме таблицы. Пояснить метод решения задачи.

 

 

№ 19

Расчет и построение графика функции. Организовать вывод массива результатов расчета функции в файл и построить график этой функции на экране. Построить графики функци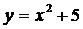й .и в интервале

x= –10...25 с шагом 0.5. Пояснить метод решения задачи.

 

 

№ 20

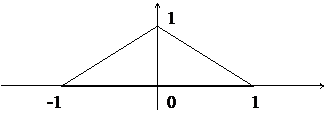Принадлежность точки заданной фигуре. Определить, принадлежит ли заданная точка фигуре, представленной на рисунке. Решить задачу для точек с координатами (-0,5; 0,8), (0,5; 0,4).

Результат вывести в графической и табл. форме.

Пояснить метод решения задачи.

 

 

 

 

№ 21

Напечатать таблицу. Напечатать таблицу соответствия между весом в фунтах и весом в килограммах для значений от 1 до 10 фунтов с шагом 1 фунт (1 фунт » 400 г.), а также таблицу перевода расстояний в дюймах в сантиметры (1 дюйм = 2,54 см.). Пояснить метод решения задачи.

 

 

№ 22

температура воздуха. Информация о температуре воздуха за месяц задана в виде массива. Определить, сколько раз температура опускалась ниже 0°С. Массив данных сформировать функцией RND из 30 чисел, представить в виде таблицы и вычертить график f(T), где Т=30 дней в апреле (массив данных можно взять в GISMETEO.RU). Пояснить метод решения задачи.

 

 

№ 23

Определить площадь треугольника. По известным двум углам и основанию треугольника, определить его площадь.

Выполнить рисунок треугольника, определить и вывести координаты точек вершин при a=45°, b=30°, AB =100. Сделать программу в форме диалога. Пояснить метод решения задачи.

 

№ 24

 

Сколько дней прожито. Определить сколько дней прожито от дня рождения до сегодня. Нанести на числовую ось результат в пределах экрана. Пояснить метод решения задачи.

 

 

№ 25

 

Простые числа. Напечатать все простые числа, не превосходящие заданное М (например, М = 111). Результат представить в графической форме и нанести все простые числа на числовую ось (в масштабе в пределах экрана). Пояснить метод решения задачи.

 

№ 28

 

Определение площади фигуры. Найти S фигуры ограниченной линиями x=1, x=5 параллельно оси y и кривой . Нарисовать график, вывести значение S в текстовой форме. Пояснить метод решения задачи.

 

 

 

№ 29

 

Результаты сессии. В сессию 20 студентов сдали 5 экзаменов. Результат получить через RND, вывести в виде таблицы, подсчитать средний балл по каждому предмету и студенту. Вывод организовать в виде диаграммы. Пояснить метод решения задачи.

 

 

№ 30

 

Нахождение «седлового» элемента. Задан двумерный массив A(m; n), некоторый элемент назовем «седловой», если он одновременно наибольший в своем столбце и наименьший в своей строке. Напечатать номер строки и столбца этого элемента или «0» если его в массиве нет. Привести примеры для обеих ситуаций и результат вывести в виде таблицы. Пояснить метод решения задачи.

 

 

№ 31

Ввести число n и заполнить двумерный массив размером n´n числами 1, 2, 3... n² по спирали. Вычертить рисунок. Пояснить метод решения задачи.

 

№ 33

 

Повторяющееся число в массиве. В целочисленном массиве A(n) n=20 найти число, которое повторяется максимальное количество раз. Если их несколько, то вывести оба или одно. (2 варианта). Массив сформировать функцией RND. Если нет повторяющихся чисел, то их ввести в массив. Указать номера повторяющихся компонентов. Пояснить метод решения задачи.

 

 

№ 32

 

Счёт штрафного времени. Составить программу, суммирующую штрафное время команд при игре в хоккей. В программе предусмотреть ввод названий команд в виде символьных переменных и вывод их на экран в итоговом сообщении.

При очередном удалении нужно вводить в ЭВМ название команды, игрок которой удален, и время, на которое он удален. Так как название команды состоит из нескольких символов, то для облегчения ввода их можно закодировать. Например, цифрами 1 и 2. Код команды и время удаления вводить различными операторами ввода. Для окончания ввода использовать значение того же типа, что и код команды (в нашем случае число). Пояснить метод решения задачи.

 

 

№ 34

 

Имеется «К» селений. Если в селении ί расположить пункт скорой помощи, то поездка по вызову в селение ј займет время A(ί; ί) + А(ί; ј) при (1 £ ί, ј £ к, ί ¹ ј). Найти номер селения ί, от которого поездка в самое удаленное (по времени) селение занимала бы минимальное время. Массив А(6´6) заполнить таким образом, что А(ί; ј)> 0 и А(ί; ј) не равен А(ј; ί). Вычертить схему и выделить цветом селение, где расположена скорая помощь.). Пояснить метод решения задачи.

 

 

№ 35

 

Определить, поместится ли квадрат в круг. Задана площадь круга R и квадрата S. Определить, поместится ли квадрат в круг и круг в квадрате при исходных данных:

R		0,86	3,2	3,2	6,0
S	36,74	0,64	3,5	4,0	9,0

Данные можно добавлять и изменять, чтобы

Найти при какой R=Const в нее поместится

Заданное S и наоборот. Выполнить рисунок. Пояснить метод решения задачи.

 

 

№ 36

 

Найти порядковый номер. Сформировать с помощью функции RND массив из 100 элементов. Найти все равные и их порядковые номера. Пояснить метод решения задачи.

 

 

№ 37

 

Точка и кольцо. В ЭВМ поочередно вводятся координаты n точек. Определить сколько из них попадет в кольцо с внутренним радиусом R1 и внешним R2. выполнить рисунок. Точки вводить в диалоговом режиме любым способом (INPUT, DIM N(**,**), DATA) и отобразить на рисунке заштрихованным кругом. Пояснить метод решения задачи.

 

 

 

№ 38

 

Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый следующий день он увеличивал норму на 10 % от нормы предыдущего дня. Через 15 дней он увеличил норму на 20 %. Какой суммарный путь пробежит спортсмен за 27 дней? Результат изобразить в виде графика на числовой оси и в виде текстового сообщения. Пояснить метод решения задачи.

 

 

№ 39

 

Траектория снаряда. Траектория снаряда, вылетающего из орудия под углом a с начальной скоростью u₀, описывается уравнениями:

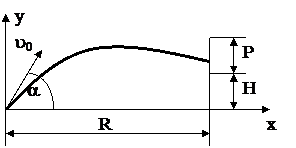
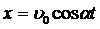, , где g = 9,8 м/с² – ускорение свободного падения, t – время. Вводя n заданных пар u₀, a, определить, сколько снарядов поразит цель высотой Р, расположенную в вертикальной плоскости ствола орудия на расстоянии R на высоте Н (см. рис., вывести.

его на экран). Результат в виде табл.

Пояснить метод решения задачи.

 

 

 

 

№ 40

 

Составить универсальную программу решения квадратного и кубического уравнения с любыми коэффициентами. Коэффициенты и результаты вывести в виде таблицы. Пояснить метод решения задачи.

 

 

№ 43

 

Наибольшее и наименьшее число. Найти наибольшее и наименьшее число в одномерном массиве и определить количество элементов в массиве с шагом k = 10.

Пример: 16, 8, 23, 11, 68, 63, 18.

max – 68; min – 8

1 отрезок 1-10 – 1 элемент, (8)

2 отрезок 10-20 – 2 элемента, (11 и 16) и т.д. Пояснить метод решения задачи.

 

 

№ 45

 

Формирование массива чисел. Сформировать одномерный массив из 25 элементов. Все ненулевые элементы переписать в начало, а нулевые – в конец этого же массива. Новый массив не заводить. Пояснить метод решения задачи.

 

 

№ 46

 

Нахождение наибольшего и наименьшего. Найти наибольшее и наименьшее из трех задаваемых чисел и расположить их на числовой оси в масштабе в пределах экрана. Пояснить метод решения задачи.

 

 

 

№ 47

 

График тренировки спортсмена. Начав тренировки спортсмен в первый день пробежал 10 км. Каждый следующий день он увеличивал дневную норму на 10 % от нормы предыдущего дня. Какой путь пробежал спортсмен за 7, 10, 15 дней. Через сколько дней он будет бежать 20 км и прекратит увеличивать норму.

Результат в виде диаграммы и текстового сообщения. Пояснить метод решения задачи.

 

 

№ 48

 

Стрельба из орудия. Траектория снаряда, вылетающего из орудия под углом a с начальной скоростью u₀, описывается уравнениями:

,

,

где g = 9,8 м/с², a = p/4, u₀ = 30 км/мин.

С точностью до D х = 2 км определить, точку (расстояние), в которой снаряд уйдет под землю. Нарисовать схему. Напечатать результат. Пояснить метод решения задачи.

 

 

№ 49

 

Построение графиков стандартных функций. Разработать универсальную программу построения графиков стандартных функций (примечание: для стандартных функций создать меню из 4-х функций по выбору):

Функции: e^x, e^-x, 1-e^x, 1-e^-x, lg x, ln x, 1+e^x, 1+e^-x, sin x, cos x, x², 1+x², 1-x², x²-1,

ax²+bx+c. Пояснить метод решения задачи.

 

 

№ 50

 

Стоимость платья. Стоимость платья зависит от материала и модели. На складе ателье 2 вида материала: шерсть по 300 руб. за 1 м и шелк по 160 руб. за 1 м. На пошив одного платья требуется 3 м ткани, стоимость работ по пошиву – 100 руб. (без отделки). За дополнительные детали плата: 1 пуговица – 2 руб., 1 складка на юбке – 15 руб. Составить программу определения дохода ателье: при плане 100 платьев изготавливается по 3 платья 6 новых фасонов, остальные базовые. Построить диаграмму. Пояснить метод решения задачи.

 

 

№ 52

 

Загрузка самолёта. Самолет может подняться в воздух при взлетном весе 30 тонн. Составить таблицу загрузки самолета для грузовой службы аэропорта при следующих случаях: 25% пассажиров + груз =?

50% пассажиров + груз =?

75% пассажиров + груз =?

100% пассажиров + груз =?

Вес пассажира 75 кг, его багаж 20 кг. Напечатать таблицу и график. Пояснить метод решения задачи.

 

№ 53

 

Сгенерировать функцией RND 10 пар чисел – условно площадей круга и треугольника. Определить разность площадей круга и вписанного в него равностороннего треугольника и наоборот. Результаты вывести в виде таблицы, выполнить рисунок. Пояснить метод решения задачи.

 

 

 

 

№ 54

Построить график 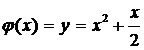Определить площадь в пределах

Вычертить график. Программу создать универсальную, т. е. записывается в подпрограмму, а предел вводить по IMPUT. Пояснить метод решения задачи.

 

 

 

№ 56

 

Напечатать таблицу умножения от 1 до 10 по диагонали (т.е. исключить все повторы типа 1х1=10 и 10х1=10). Пояснить метод решения задачи.

 

 

 

№ 57

 

Плотность воздуха убывает с высотой по закону считая, что

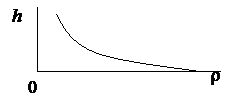r₀= 1,29 кг/м³, z= 1,25×10^-4 1/м напечатать таблицу зависимости плотности от высоты для значений от 0 до 10000 м. С шагом 500 м. И построить график. Пояснить метод решения задачи.

 

 

№ 60

 

, если i не четная

, если i четная

Сформировать массив М(20) по правилу

 

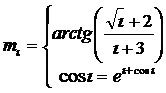
i =0, 1, 2... 20 найти минимальный элемент и его номер в массиве.

Результат ввести в виде таблицы. Построить графики 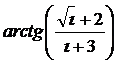и cosi.

Пояснить метод решения задачи.

 

 

№ 61

 

Дан массив P = {2,6; 3,3; 1,8; 5,6; -3,8; -4,2} Выделить из массива P новый массив R меньшей размерности по правилу: элемент массива P переносится в R если квадратное уравнение имеет единственные и различные корни. Решить для q = 2, 4, 6, 8. Результат в виде таблицы. Пояснить метод решения задачи.

 

 

№ 62

 

Функция y = f(x) задана таблично (дискретная функция).

x		0,5	1,5	2,1	3,5		7,5			15,2
y	1,5	-1	-3	-2,6		2,6	7,5		-2,5	-1,5

Определить координаты точек y_i, если x_i принадлежат значения:

0,3; 1,1; 1,95; 2,87; 4,01; 7; 0,685; 9,5; 15,18.

Вычертить y = f(x), и результат в таблице. Пояснить метод решения задачи.

 

 

№ 63

 

Во время эксперимента измерения температуры двигателя получены следующие результаты

t, мин
T°C			28,2	35,05		45,3	50,15	55,2		60,02	60,05	60,1	60,1

 

Найти значение температуры в серединах интервалов измерений и погрешности результатов в виде таблицы и графика T = f(t). Пояснить метод решения задачи.

 

 

№ 64

 

Сформировать два массива А(12) и В(12) пользуясь соотношениями , Получить третий массив по правилу

i = 1,2 – 12, j = 1,2 – 12, k = 1,2 – 12. Подсчитать сумму элементов массива. Результат в виде таблицы, сумма в виде фигур в масштабе. Пояснить метод решения задачи.

 

 

№ 65

 

Вычислить значение многочлена по формуле Горнера для

x = 0,25; 0,5; 0,75; 1; 1,25.

Построить график y = f(x). Пояснить метод решения задачи.

 

 

№ 67

 

Сформировать одномерный массив А(50), выбрать из него все положительные числа и создать новый массив В по правилу:

b₁ = a₁ , b₂ = a₂ , b₃ = a₃+a₁ , b₄ = a₄+a₂…

Подсчитать сумму членов старого и нового массива. Результат записать в виде таблицы с элементами обеих массивов и сумм. На графике в масштабе фигур изобразить сумму. Пояснить метод решения задачи.

 

 

 

№ 68

В ЭВМ вводятся по очереди координаты n точек. Определить, сколько из них попадет в круг радиусом R с центром в точке (a, b). Вывод в графической и символьной форме. Пояснить метод решения задачи.

 

 

 

 

№ 69

Создать программу вычисления суммы , где Р равно произведению

Разместить Р_j на числовой оси в удобном масштабе и в виде таблицы P, S = f(n). Пояснить метод решения задачи.

 

 

№ 70

 

Ввести координаты (x, y) точки М и определить принадлежит ли точка М фигуре на рисунке или нет. Результаты 5 попыток задания координат М(x, y) парой чисел RND функции представить в таблице и на рисунке. Пояснить метод решения задачи.

 

 

 

 

№ 72

Составить программу вычисления A = sin T, если Т>0; 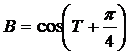, если Т<0; С = 1 если Т = 0, где 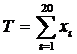; x_i генерировать RND. Результаты 5 попыток оформить таблицей. Пояснить метод решения задачи.

 

 

 

№ 73

 

, если a£0

, если a>0

Вычислить значение функции

 

Где x_max и x_min элементы массива x₁, x₂ …x_n; y_max элементы массива y₁, y₂ …y₂ Массивы x_j, y_j задать по 10 элементов. Пояснить метод решения задачи.

 

 

№ 74

 

Составить программу вычисления функции , где S1 и R1 – сумма и количество положительных элементов массива (а1, а2,..., а20), S2 и R2 - то же массива (b1, b2,..., b10). Массивы сформировать функцией RND. Пояснить метод решения задачи.

 

 

№ 75

 

Сформировать функцией RND массив А (15). Все отрицательные числа заменить на их квадраты, а положительные на нули. Подсчитать суммы обоих массивов. Напечатать в виде таблицы оба массива. Площади изобразить в виде фигур в масштабе. Пояснить метод решения задачи.

 

 

№ 76

 

С помощью функции RND сформировать массив из 30 положительных чисел. Определить есть ли в массиве 4 числа идущие подряд (например, 1, 2, 3, 4 или 7, 15, 20, 40), то есть между ними нет других чисел.

Вывести их на печать. Нанести на числовую ось в масштабе. Сделать 5 попыток. Результат представить в виде таблицы. Пояснить метод решения задачи.

 

№ 77

 

В ЭВМ по очереди вводят координатыn точек. Определить, сколько из них принадлежит фигуре, ограниченной осью абсцисс и аркой синусоиды, построенной для аргумента от 0 до p. Пояснить метод решения задачи.

 

 

 

№ 78

 

Два треугольника заданы координатами вершин:

А₁ (1; 1); В₁ (4; 2); С₁ (2; 3,5): D 1

А₂ (1; 2); В₂ (4; 1); С₂ (3; 3,5): D 2

Вычислить длины сторон и площади по формуле Герона. Определить больший треугольник. Вычертить D 1 и D 2, и заштриховать разным цветом. Пояснить метод решения задачи.

 

 

№ 79

 

Пять спортсменов стартуют одновременно из одной точки с начальными скоростями 10; 9,5; 9,25; 9,0; 8,5 км/ч и равномерно (линейно) за каждый следующий час увеличивают свою скорость на 1; 1,2; 1,4; 1,6; 1,8 км/ч соответственно. Выяснить, какие спортсмены будут друг от друга на максимальном и минимальном расстоянии через 2,25 часа и 4,0 часа.

Пояснение: матрицы расстояний между спортсменами, поиск максимальных и минимальных расстояний оформить отдельными подпрограммами. Нарисовать положения спортсменов. Пояснить метод решения задачи.

 

 

№ 80

 

Два треугольника заданы своими сторонами a, b, c (даны длины сторон). Вычислить площадь треугольников по формуле Герона и определить, какой треугольник имеет большую площадь. Вычертить треугольники 1 и 2 в масштабе и заштриховать разным цветом.

Дано: треугольник 1: a₁ = 3, b₁ = 4, c₁ = 5: треугольник 2: а₂ = 2, b₂ = , c₂ = .