Вариант №1
Случайные события (часть 1)
Задачи 1, 2 решить с помощью формул комбинаторики.
- На 10 одинаковых по форме и размеру каточках написаны буквы слова математика – по одной букве на каждой карточке. Карточки тщательно перемешаны. Их вынимают наудачу и располагают на столе одна за другой. Какова вероятность снова получить слово математика?
- В ящике находится 6 красных, 8 голубых и 16 зеленых шаров. Наудачу вынимают 9 шаров. Какова вероятность того, что вынуты 2 красных, 3 голубых и 4 зеленых шара?
- На отрезке единичной длины наудачу появляется точка. Определить вероятность события А – расстояние от точки до концов отрезка превосходит величину 1/4.
Задачи 4,5,6 решить с помощью теорем сложения и умножения вероятностей.
- Вероятность попадания в цель для первого спортсмена 0,9 для второго 0,85. Спортсмены независимо друг от друга сделали по одному выстрелу. Найти вероятность того, что в результате этих выстрелов окажется
а) ни одного попадания;
б) хотя бы одно попадание;
в) ровно одно попадание;
г) ровно два попадания.
- В урне находятся 9 красных и 7 голубых шаров. Из урны последовательно без возвращения извлекают 3 шара. Найти вероятность того, что все три шара голубые.
- Вероятность того, что событие появится хотя бы один раз в трех независимых испытаниях, равна 0,936. Найти вероятность появления события в одном испытании (предполагается, что во всех испытаниях вероятность появления события одна и та же).
Вариант №2
Случайные события (часть 1)
Задачи 1, 2 решить с помощью формул комбинаторики.
- На 10 одинаковых по форме и размеру каточках написаны буквы слова менеджмент – по одной букве на каждой карточке. Карточки тщательно перемешаны. Их вынимают наудачу и располагают на столе одна за другой. Какова вероятность снова получить слово менеджмент?
- Среди 25 студентов группы, в которой 8 девушек разыгрываются 5 билетов в кино. Найти вероятность того, что среди обладателей билетов окажется 2 девушки.
- Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов независимо и равновозможно в течение данных суток. Определить вероятность того, что одному из пароходов придется ожидать освобождения причала, если время стоянки первого парохода - один час, а второго - два часа.
Задачи 4,5,6 решить с помощью теорем сложения и умножения вероятностей.
- Стрелок производит 3 выстрела. Вероятности попадания при первом, втором и третьем выстрелах соответственно равны 0,7; 0,8; 0,9. Найти вероятность того, что в результате этих выстрелов окажется
а) ни одного попадания;
б) хотя бы одно попадание;
в) ровно одно попадание;
г) ровно три попадания.
- Подбрасываются два игральных кубика. Найти вероятность события А- сумма выпавших очков не превосходит 4.
- В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятности отказов первого, второго и третьего элементов соответственно равны: 0,15; 0,2; 0,25. Найти вероятность того, что тока в цепи не будет.
Вариант №3
Случайные события (часть 1)
Задачи 1, 2 решить с помощью формул комбинаторики.
- На 9 одинаковых по форме и размеру каточках написаны буквы слова маркетинг – по одной букве на каждой карточке. Карточки тщательно перемешаны. Их вынимают наудачу и располагают на столе одна за другой. Какова вероятность снова получить слово маркетинг?
- В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди 6 взятых наудачу деталей 4 стандартных.
- В квадрат с вершинами
наудачу брошена точка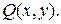 
Какова вероятность того, что координаты этой точки удовлетворяют неравенству 
Задачи 4,5,6 решить с помощью теорем сложения и умножения вероятностей.
- В мастерской два мотора работают независимо друг от друга. Вероятность того, что в течение дня первый мотор не потребует ремонта, равна 0,8, а для второго мотора эта вероятность равна 0,7. Найти вероятность того, что в течение дня
а) ни один мотор не потребует ремонта;
б) хотя бы один мотор потребует ремонта;
в) ровно одно мотор потребует ремонта;
г) оба мотора потребуют ремонта.
- Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,46. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0,9.
- Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,04 и 0,05. Найти вероятность отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.
Вариант №4