Явление электромагнетизма было открыто в 1820 году датским физиком
Г.Х. Эрстедом, суть которого состоит в том, что при протекании по проводнику электрического тока вокруг последнего образуется магнитное поле.
Был установлен закон электромагнетизма: потокосцепление электрической катушки прямо пропорционально силе электрического тока и индуктивности катушки.
Математическая запись закона электромагнетизма следующая:
 ,
| (3.1) |
где y – потокосцепление катушки, Вб;
Ф – число витков катушки;
L – индуктивность катушки, Гн;
i – сила электрического тока в катушке, А.
Представим описанное явление схематически (рис.3.1).
Явление электромагнитной индукции открыл в 1831 году английский физик Майкл Фарадей, суть которого состоит в следующем: если проводящий контур пронизывается переменным магнитным потоком, то в контуре индуктируется (наводится) электродвижущая сила.
Закон электромагнитной индукции: значение электродвижущей силы, наводимой в контуре, прямо пропорционально числу витков контура и скорости
изменения магнитного потока.
Математическая запись закона:
 ,
| (3.2) |
где е – электродвижущая сила, В;
w – число витков катушки;
Ф – магнитный поток, Вб;
t – текущее время, с.
 .
|
Пример 3.1
Катушка, состоящая из 100 витков, имеет индуктивность 0,1 Гн;
по катушке протекает ток i = 10 sin wtА.
Определить магнитный поток внутри катушки.
Решение.
Из (3.1) находим магнитный поток:
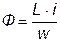. (3.1 а)
Подставляем значения физических величин и получаем:
.
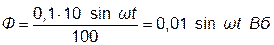Физический смысл знака «минус» состоит в следующем: если в данный
момент времени магнитный поток, пронизывающий контур, увеличивается, то он наводит э.д.с., которая создаст электрический ток, а последний свой магнитный поток, который будет направлен против основного потока и наоборот.
|
|
Рассмотрим это на графике (рис.3.2).
Явления электромагнетизма и электромагнитной индукции лежат в основе принципа действия генераторов переменного
синусоидального тока.
Приведём вариант конструктивной схемы генератора переменного синусоидального тока (рис.3.3).
Магнитный поток создается током
намагничивания I. Проводящий контур (рамка) помещается на оси между полюсами электромагнита. Если рамку привести во вращение, то
магнитный поток, пронизывающий рамку, будет изменяться во времени по синусоидальному
закону и в рамке будет наводиться э.д.с., которая также будет изменяться по синусоидальному
закону в зависимости от угла отклонения рамки от горизонтального положения (рис.3.2, 3.3), т.е.
| е = E m ×sin a, | (3.3) |
где Е m – амплитудное (максимальное)
значение э.д.с. (при вертикальном
положении рамки), В;
a – угол отклонения рамки
от горизонтального положения, рад (град);
e – мгновенное значение э.д.с.
для заданного угла отклонения рамки, В.
Угол отклонения рамки зависит во времени от угловой скорости вращения рамки:
| a = w × t, | (3.4) |
где w – угловая скорость вращения рамки, рад/с (град/с);
t – текущее время, с.
Таким образом, подставив (3.4) в (3.3), получим зависимость э.д.с. от угловой скорости вращения рамки:
| е = E m × sin w t, | (3.5) |
Пример 3.2
Катушка индуктивности, состоящая из 100 витков,
пронизывается магнитным потоком ф = 0,01 sin wtВб, w = 314 с –1.
Определить электродвижущую силу, которая наводится в катушке.
|
|
Решение.
Подставляем значения физических величин в (3.2) и получаем:
.
Если рамку замкнуть с помощью щёточного механизма на резистор, то
возникает синусоидальный ток:
| i = I m × sin w t, | (3.6) |
где I m – амплитудное (максимальное) значение тока
(при амплитудном значении э.д.с.), А;
i – мгновенное значение тока, А.
Покажем график i = f(t) на рис.3.4.
Запишем угловую скорость вращения рамки через частоту (количество оборотов в секунду):
| w = 2p × f, | (3.7) |
где f – частота вращения рамки, (1/ с) Гц.
С такой же частотой f будет изменяться и электрический ток.
Время одного оборота рамки обозначим через Т; таким же будет и время
одного полного колебания тока, назовём его периодом тока.
В Европе частота тока равна 50 Гц, т.е. f = 50 Гц (1/ с).
Тогда период тока Т = 0,02 с, т.е.
 .
| (3.8) |
В общем случае в момент времени t = 0 рамка может находиться под определённым углом по отношению к горизонтальному положению и тогда мгновенное значение тока записывается следующим образом:
| i = I m×sin(w t + y i), | (3.9) |
где y i – начальная фаза тока (начальный угол отклонения рамки), рад (град);
(w t+ y i) – текущая фаза тока, рад (град).
Синусоидальные величины (токи, напряжения, э.д.с., потенциалы) изображают на плоскости с помощью векторов. Для этого берётся амплитудное значение синусоидальной величины и в выбранном масштабе откладывается в виде отрезка прямой под углом к оси отсчёта, равным начальной фазе изображаемой величины. Если начальная фаза положительная, то угол отсчёта откладывается против часовой стрелки, если отрицательная – по часовой стрелке. В качестве примера ток
i = I m × sin(w t+ 45°) А изображён на рис.3.5.
|
|
Угловую скорость вращения рамки называют круговой (угловой) частотой тока:
w =2 p × f =2 p× 50= 314 рад/с
и график i = f (t) чаще всего строят в виде i = f¢ (wt), т.е. мгновенное значение тока в функции мгновенного значения фазы тока (мгновенного угла поворота
рамки).
В виде вектора ток изображают для момента времени t = 0. Мгновенное
значение тока в любой другой момент времени (другой фазы тока) есть проекция вектора на вертикальную ось (рис.3.5).
Пример 3.3
По катушке протекает ток i = 15 sin (wt +30°) А.
Изобразить ток в виде вектора.
Решение.
Выбираем масштаб тока mi = 0,5 А/мм и строим вектор тока (рис.3.6).
Сопротивление проводника переменному току (активное) зависит от частоты тока и связано с тем, что в результате вытеснения тока на поверхность проводника сечение проводника как бы уменьшается, что приводит к увеличению его сопротивления по сравнению с постоянным током. Вытеснение тока на поверхность проводника (поверхностный эффект) объясняется явлением электромагнитной индукции. Переменное магнитное поле вокруг проводника, созданное переменным током в проводнике, наводит э.д.с. самоиндукции. Если представить проводник состоящим из множества параллельных нитей, по которым проходят свои токи, то самое большое число магнитных силовых линий сцеплено с центральными нитями и там наводится самая большая э.д.с., которая препятствует току и вытесняет его на поверхность (рис.3.7).
 |
Изображается активное сопротивление на расчётных схемах следующим образом:.
Из курса физики известно, что индуктивность катушки (проводника) зависит от квадрата числа витков, магнитной проницаемости среды, по которой замыкается магнитный поток, площади внутреннего сечения катушки и длины средней силовой линии магнитного потока, т.е.
 ,
| (3.10) |
где w – число витков катушки;
m – относительная магнитная проницаемость среды,
по которой замыкается магнитный поток;
m 0 – магнитная постоянная (m 0 = 4p×10–7 Гн/м), Гн/м;
S – площадь внутреннего сечения катушки, м 2;
l – длина средней магнитной силовой линии, м.
 .
|
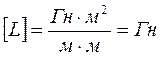Индуктивность на расчётных схемах изображается следующим образом:
.
Пример 3.4
Катушка индуктивности без ферромагнитного сердечника имеет 1000 витков.
Площадь внутреннего сечения катушки равна 400 см 2,
длина средней силовой линии магнитного потока катушки равна 12,56 см.
Определить индуктивность катушки.
Решение.
Подставляем значения параметров катушки в (3.10) и получаем:
.
Действующее значение переменного синусоидального тока.
Переменный синусоидальный ток, проходя по проводнику, сопровождается тепловым действием независимо от направления тока. Мгновенная мощность, выделяемая в проводнике
| р = r × i 2, | (3.11) |
где r – активное сопротивление, Ом;
i – мгновенный ток, А;
р – мгновенная мощность, Вт.
Найдём количество тепла (энергии), которое выделится в проводнике за период тока:
 .
| (3.12) |
Заменим действительный переменный синусоидальный ток эквивалентным
постоянным током, при котором за период выделится такое же количество тепла в том же проводнике:
| W = r × I 2× T, | (3.13) |
где I – эквивалентный постоянный ток, А.
Приравняв (3.12) с (3.13), находим:
 .
| (3.14) |
Величину эквивалентного постоянного тока назвали действующим значением переменного синусоидального тока. По аналогии введём понятия действующих значений э.д.с. и напряжения:
 ;
| (3.15) |
 .
| (3.16) |
Электроизмерительные приборы показывают действующие значения измеряемых величин (тока, напряжения).
Пример 3.5
В цепи протекает электрический ток i = 14,1 sin (wt –37°) А.
Определить показание амперметра, включённого в цепь.
Решение.
Амперметр показывает действующее значение тока, которое определяем по (3.14), подставив амплитуду тока:
.
Вопросы для самоконтроля
1. В чём суть явления электромагнетизма?
2. Сформулируйте закон электромагнетизма.
3. Математически запишите и расшифруйте закон электромагнетизма.
4. В чём суть явления электромагнитной индукции?
5. Сформулируйте закон электромагнитной индукции.
6. Математически запишите и расшифруйте закон электромагнитной индукции.
7. Поясните физический смысл знака «минус».
8. Приведите пример использования явления электромагнитной индукции в технике.
9. Составьте и опишите конструктивную схему машинного генератора
переменного синусоидального тока.
10. Опишите принцип действия машинного генератора переменного синусоидального тока.
11. Объясните, почему в генераторе наводится синусоидальная э.д.с.,
запишите и расшифруйте её математическое выражение.
12. Запишите и расшифруйте математическое выражение
мгновенного напряжения на зажимах идеального генератора.
13. Как получить синусоидальный ток?
14. Запишите и расшифруйте математическое выражение
мгновенного синусоидального тока.
15. Что такое амплитуда тока?
16. Что такое частота тока?
17. Что такое период тока?
18. Что такое круговая частота тока?
19. Что такое начальная фаза тока?
20. Что такое мгновенная фаза тока?
21. Как изобразить ток с помощью радиус-вектора?
22. Объясните физический смысл активного сопротивления проводника переменному току по сравнению с сопротивлением проводника постоянному току.
23. Что такое индуктивность катушки? От чего она зависит?
24. Что понимается под действующим значением переменного синусоидального тока?
Как его рассчитать через амплитудное значение тока?
25. Как рассчитать действующее значение э.д.с. через амплитудное значение?
26. Как рассчитать действующее значение напряжения через амплитудное значение?
Задания для самоконтроля
В цепи протекает ток i = 28,2sin (wt – 30°) А.
1. Изобразите этот ток графически в виде i = f (wt).
Укажите на графике период и амплитуду тока.
2. Изобразите этот ток с помощью радиус-вектора.
3. Найдите показание амперметра, по которому протекает указанный ток.
3.2. Цепь переменного синусоидального электрического тока
с резистором
Составим принципиальную электрическую схему цепи с резистором (рис.3.8).
 |
Г – генератор синусоидальной э.д.с.;
РА – амперметр;
R – резистор.
Принимаем генератор идеальным (не имеющим активного сопротивления и индуктивности), сопротивлением амперметра и соединительных проводов пренебрегаем
и составляем расчётную схему этой цепи:
в генераторе индуктируется э.д.с., в цепи протекает ток, в резисторе наблюдается
тепловое действие тока (рис.3.9).
Пусть мгновенное значение э.д.с.
описывается следующим выражением:
| е = E m×sin wt. | (3.17) |
Напряжение на зажимах генератора будет зависеть от э.д.с. и запишется так:
| u r= е, u r= U rm × sin wt, U rm= E m. | (3.18) (3.19) (3.20) |
Мгновенный ток в цепи в соответствии с законом Ома для замкнутой цепи:
 ;
| (3.21) (3.22) |
.Подставляем выражение напряжения (3.19) и получаем:
 ,
| (3.23) (3.24) |
.Для действующих значений:
 .
| (3.25) |
Покажем напряжение и ток в цепи с резистором (на участке цепи с активным сопротивлением) графически (рис.3.10).
 |
Введём понятие угла сдвига фаз, под которым будем понимать абсолютное значение разности начальных фаз напряжения и тока:
| j = | y ur – y i|, | (3.26) |
где j – угол сдвига фаз, рад (град);
y ur – начальная фаза напряжения, рад (град);
y i – начальная фаза тока, рад (град).
Для участка цепи с активным сопротивлением, как видно из (3.19), (3.23) и рис.3.9, угол сдвига фаз равен нулю, т.е. напряжение и ток на участке цепи с
активным сопротивлением совпадают по фазе: j = 0.
Найдём выражение мгновенной мощности:
| (3.27) |
Введём понятие активной мощности, под которой будем понимать среднее значение мощности за период. Найдём выражение активной мощности:
 .
| (3.28) |
Подставив выражение тока (3.23) в (3.28) и преобразовав, получаем:
 .
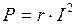| (3.29) |
Таким образом, мгновенная мощность в активном сопротивлении
 .
| (3.30) |
Она всегда положительна, то есть направлена от источника к приёмнику.
Представим эту зависимость графически (рис.3.11).
 |
Заштрихованная площадь на рис.3.11 представляет собой энергию, которая
выделяется в резисторе за период:
 .
| (3.31) |
Таким образом, активная мощность – это энергия, которая выделяется в активном сопротивлении за единицу времени:
 .
| (3.32) |
Пример 3.6
К резистору подведено напряжение u r = 141 sin (wt –30°) В.
Активное сопротивление резистора равно 100 Ом.
Выполнить анализ участка цепи.
Решение.
1. Определяем амплитуду тока по (3.24):
.
2. Определяем начальную фазу тока:
y i = y ur = – 30°.
3. Записываем мгновенный ток:
i = 1,41 sin (wt –30°) А.
4. Определяем действующее значение тока по (3.14):
.
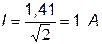5. Определяем активную мощность по (3.32):
Р = 100×12 = 100 Вт.
Вопросы для самоконтроля
1. Опишите физические явления, наблюдаемые в резисторе
в цепи переменного синусоидального тока
2. Составьте расчётную схему цепи с идеальным генератором и резистором.
3. Запишите математическую связь между мгновенным напряжением,
мгновенным током и активным сопротивлением.
4. Сформулируйте и математически запишите закон Ома для максимальных
и действующих значений напряжения и тока на участке цепи с резистором.
5. Запишите математическое выражение мгновенного напряжения
на активном сопротивлении, приняв начальную фазу равной нулю.
6. Запишите математическое выражение мгновенного тока в активном сопротивлении для указанного выше напряжения.
7. Постройте графически оригиналы мгновенного напряжения и мгновенного тока
на участке цепи с резистором.
8. Изобразите напряжение и ток с помощью векторов.
9. Что понимается под углом сдвига фаз? Чему он равен на участке цепи с резистором?
10. Получите математическое выражение мгновенной мощности в резисторе.
С какой частотой колеблется мгновенная мощность в резисторе?
11. Что понимается под активной мощностью? Как её рассчитать в резисторе?
Укажите её единицу.
Задания для самоконтроля
К резистору подведено напряжение u r = 282sin (wt + 47°) В.
Активное сопротивление резистора r = 10 Ом.
1. Записать выражение мгновенного тока.
2. Найти активную мощность в резисторе.
3. Записать выражение мгновенной мощности в резисторе.
4. Изобразить графически мгновенный ток и мгновенную мощность в функции wt.
3.3. Цепь переменного синусоидального тока
с идеальной катушкой
Под идеальной катушкой будем понимать такую, у которой активное сопротивление равно нулю. Включим её в цепь с идеальным генератором синусоидальной э.д.с. (рис.3.12).
 |
Г – генератор синусоидальной э.д.с.;
РА – амперметр;
К – катушка.
Составим расчётную схему цепи, пренебрегая сопротивлением амперметра и соединительных проводов: генератор вырабатывает синусоидальную э.д.с., переменный ток в катушке создает переменное магнитное поле (рис.3.13). Будет наблюдаться явление электромагнитной индукции (самоиндукции) и в катушке будет индуктироваться э.д.с. e L (рис.3.14).
Запишем уравнение электрического равновесия цепи по второму закону Кирхгофа:
| e + e L = 0, e = u L, тогда u L=– e L. | (3.33) (3.34) |
Э.д.с. самоиндукции, которая наводится в катушке, зависит от числа витков
катушки w и скорости изменения магнитного потока:
 .
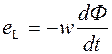| (3.35) |
С учётом (3.1) можем записать:
 .
| (3.36) |
Подставляем (3.36) в (3.34) и получаем:
 .
| (3.37) |
Полученное выражение устанавливает связь между напряжением и током
в индуктивности.
Зададимся током в цепи
| (3.38) |
и найдём, каким должно быть напряжение на зажимах генератора при таком токе:
 ,
| (3.39) (3.40) |
.
Величину wL обозначим x L и назовём реактивным сопротивлением катушки, то есть
| x L = w×L, | (3.41) |
Проверим единицу этого сопротивления:
 .
|
Запишем закон Ома для максимальных значений, исходя из выражений (3.40) и (3.41) для участка цепи с индуктивностью:
 ;
| (3.42) (3.43) |
.Запишем закон Ома для действующих значений:
 ;
 .
| (3.44) (3.45) |
Представим графически напряжение и ток в индуктивности (рис.3.15).
Найдём угол сдвига фаз между напряжением и током в индуктивности:
| j = | y uL– y i| = |0– (–90°)| = 90°. |
Таким образом, ток в индуктивности отстаёт от напряжения по фазе на угол 90°.
Найдём мгновенную мощность в индуктивности:
| (3.46) (3.47) |
.Величину Q L назвали реактивной мощностью катушки, в качестве единицы введено:
| [ Q L] = вар. |
Активная мощность в индуктивности как среднее значение мощности
за период:
 .
| (3.48) |
Таким образом, энергия в индуктивности не выделяется в виде тепла, а происходит обмен энергией между источником и приёмником.
Рассмотрим этот процесс на графике (рис.3.14). В первую четверть периода,
когда ток возрастает, увеличивается магнитный поток и магнитное поле накапливает энергию (положительная заштрихованная площадь), мгновенная мощность
положительная и направлена от источника к приёмнику. Во вторую четверть
периода, когда ток снижается, магнитный поток уменьшается и магнитное поле
отдаёт энергию источнику (отрицательная заштрихованная площадь), мгновенная мощность отрицательна и направлена от приёмника к источнику.
Таким образом, мгновенная мощность колеблется с двойной частотой – за половину периода тока мгновенная мощность совершает полное
колебание.
Пример 3.7
К идеальной катушке подведено напряжение u L = 141 sin (wt +73°) В.
Частота тока в сети равна 50 Гц. Индуктивность катушки равна 12,7 мГн.
Выполнить анализ участка цепи.
Решение.
1. Определяем индуктивное сопротивление катушки по (3.41):
х L = 2p×50×12,7×10–3 = 4 Ом.
2. Определяем амплитуду тока по (3.43):
.
3. Определяем начальную фазу тока:
y i = y uL – 90 = 73 – 90 = –17°.
4. Записываем мгновенный ток:
i = 35,25 sin (wt –17°) А.
5. Определяем действующее значение тока по (3.14):
.
6. Определяем реактивную мощность по (3.47):
Q L = 4×252 = 2500 вар = 2,5 квар.
Вопросы для самоконтроля
1. Опишите физические явления, наблюдаемые в идеальной катушке
в цепи синусоидального тока.
2. Составьте расчётную схему цепи с идеальным генератором и идеальной катушкой.
3. Запишите математическую связь между мгновенным напряжением,
мгновенным током и индуктивностью в идеальной катушке.
4. Объясните физический смысл индуктивного сопротивления.
Как рассчитать индуктивное сопротивление идеальной катушки?
5. Сформулируйте и математически запишите закон Ома для максимальных
и действующих значений напряжения и тока на участке цепи с индуктивностью.
6. Запишите математическое выражение мгновенного тока в индуктивности,
приняв начальную фазу равной нулю.
7. Запишите математическое выражение мгновенного напряжения на индуктивности
для указанного выше тока.
8. Постройте графически оригиналы мгновенного напряжения и мгновенного тока
на участке цепи с индуктивностью.
9. Изобразите напряжение и ток с помощью векторов.
10. Чему равен угол сдвига фаз в индуктивности?
11. Получите математическое выражение мгновенной мощности в индуктивности.
С какой частотой колеблется мгновенная мощность в индуктивности?
12. Чему равна активная мощность в индуктивности?
13. Как рассчитать реактивную мощность в индуктивности? Укажите её единицу.
14. Объясните физический смысл реактивной мощности в индуктивности.
Задания для самоконтроля
К идеальной катушке подведено напряжение u L = 141sin (wt + 73°) В. Индуктивность катушки равна 25,4 мГн.
Частота тока в цепи f = 50 Гц.
1. Найти реактивное сопротивление катушки.
2. Записать мгновенное значение тока.
3. Найти реактивную мощность.
4. Записать выражение мгновенной мощности в индуктивности.
5. Изобразить графически мгновенный ток и мгновенную мощность в функции wt.
3.4. Цепь переменного синусоидального тока
с идеальным конденсатором
Под идеальным конденсатором будем понимать такой, у которого активное
сопротивление равно бесконечности. Включим его в цепь с идеальным генератором (рис.3.16).
 |
Г – генератор;
РА – амперметр;
С – конденсатор.
Составим расчётную схему цепи,
приняв сопротивление амперметра и
соединительных проводов равным нулю: генератор вырабатывает синусоидальную э.д.с., переменный ток в цепи создает
переменное электрическое поле в конденсаторе (рис.3.17).
Напряжение на ёмкости
| u с= e. | (3.49) |
Зададимся током в цепи
| i = I msin (w t + 90°) | (3.50) |
и найдём, каким должно быть в этом случае напряжение на зажимах генератора.
Заряд на обкладках конденсатора
| q = C × u c, | (3.51) |
где q – заряд конденсатора, Кл;
С – ёмкость конденсатора, Ф;
u c – напряжение на конденсаторе, В.
Ток в цепи
 ,
| (3.52) | ||||
| (3.53) (3.54) |
Величину 
обозначим x с и назовем реактивным сопротивлением конденсатора, то есть
 .
| (3.55) |
Проверим единицу этого сопротивления:
 .
|
Запишем закон Ома для максимальных значений, исходя из выражений (3.54) и (3.55):
 
| (3.56) (3.57) |
Запишем закон Ома для действующих значений:
 
| (3.58) (3.59) |
Представим графически напряжение и ток в ёмкости (рис.3.18).
 |
Найдём угол сдвига фаз между напряжением и током в ёмкости:
| j = | yuС – yi | = |0–90°| = 90°. |
Таким образом, ток в ёмкости опережает напряжение по фазе на угол 90°.
Найдём мгновенную мощность в ёмкости:
| (3.60) (3.61) |
.
Величину Q с назвали реактивной мощностью ёмкости, в качестве единицы введено:
| [ Q с]= вар. |
Активная мощность в ёмкости как среднее значение мощности за период:
 .
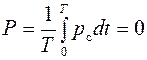| (3.62) |
Следовательно, энергия в ёмкости не выделяется, а происходит обмен энергии между источником и приёмником.
Рассмотрим этот процесс на графике (рис.3.18). В первую четверть периода,
когда напряжение на обкладках конденсатора возрастает, энергия запасается
в электрическом поле конденсатора (положительная заштрихованная площадь), мгновенная мощность положительна и направлена от источника к приемнику.
Во вторую четверть периода, когда напряжение уменьшается, электрическое поле отдает энергию источнику (отрицательная заштрихованная площадь), мгновенная мощность отрицательна и направлена от приёмника к источнику.
Таким образом, мгновенная мощность колеблется с двойной частотой – за половину периода напряжения мгновенная мощность совершает полное колебание.
Пример 3.8
К идеальному конденсатору подведено напряжение u с = 282 sin (wt – 30°) В.
Частота тока в сети равна 50 Гц. Ёмкость конденсатора равна 159 мкФ.
Выполнить анализ участка цепи.
Решение.
1. Определяем ёмкостное сопротивление конденсатора по (3.56):
.
2. Определяем амплитуду тока по (3.56):
.
3. Определяем начальную фазу тока:
y i = y uс + 90 = –30 + 90 = 60°.
4. Записываем мгновенный ток:
i = 14,1 sin (wt +60°) А.
5. Определяем действующее значение тока по (3.14):
.
6. Определяем реактивную мощность по (3.61):
Q с = 20×102 = 2 000 вар = 2,0 квар.
Вопросы для самоконтроля
1. Опишите физические явления, наблюдаемые в идеальном конденсаторе
в цепи синусоидального тока.
2. Составьте расчётную схему цепи с идеальным генератором
и идеальным конденсатором.
3. Запишите математическую связь между мгновенным напряжением,
мгновенным током и ёмкостью в идеальном конденсаторе.
4. Объясните физический смысл ёмкостного сопротивления.
Как рассчитать ёмкостное сопротивление идеального конденсатора?
5. Сформулируйте и математически запишите закон Ома для максимальных
и действующих значений напряжения и тока на участке цепи с ёмкостью.
6. Запишите математическое выражение мгновенного тока в ёмкости,
приняв начальную фазу равной нулю.
7. Запишите математическое выражение мгновенного напряжения на ёмкости
для указанного выше тока.
8. Постройте графически оригиналы мгновенного напряжения и мгновенного тока
на участке цепи с ёмкостью.
9. Изобразите напряжение и ток с помощью векторов.
10. Чему равен угол сдвига фаз в ёмкости?
11. Получите математическое выражение мгновенной мощности в ёмкости.
С какой частотой колеблется мгновенная мощность в ёмкости?
12. Чему равна активная мощность в ёмкости?
13. Как рассчитать реактивную мощность в ёмкости? Укажите её единицу.
14. Объясните физический смысл реактивной мощности в ёмкости.
Задания для самоконтроля
К идеальному конденсатору подведено напряжение
u с = 282sin (wt + 47°) В. Ёмкость конденсатора равна 318 мкФ.
Частота тока в цепи f = 50 Гц.
1. Найти реактивное сопротивление конденсатора.
2. Записать мгновенное значение тока.
3. Найти реактивную мощность в ёмкости.
4. Записать выражение мгновенной мощности в ёмкости.
5. Изобразить графически мгновенное напряжение и мгновенную мощность
в функции wt.