Включим катушку в цепь переменного синусоидального тока. Генератор
принимаем идеальным, сопротивлением соединительных проводов пренебрегаем.
В катушке наблюдаются следующие физические явления и процессы:
– под действием синусоидальной э.д.с. источника в катушке протекает ток i;
– наблюдается тепловое действие тока и катушка нагревается;
– переменный синусоидальный ток создает переменное магнитное поле, которое пронизывает эту же катушку – наблюдается явление электромагнитной индукции (самоиндукции) и в катушке наводится э.д.с. самоиндукции e L.
Составим расчётную схему катушки (рис.3.19).
Запишем уравнение электрического равновесия для этой цепи:
 
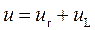
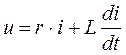
| (3.63) (3.64) |
Зададимся током в цепи
| (3.65) |
и найдём, каким должно быть в этом случае приложенное напряжение u, для чего подставим значение тока в (3.64):
 .
| (3.66) |
Обозначим согласно (3.24) и (3.40)
| (3.67) (3.68) |
и перепишем уравнение (3.66) в следующем виде:
 .
| (3.69) |
Запишем мгновенное приложенное напряжение в общем виде:
 .
| (3.70) |
Построим векторную диаграмму тока и напряжения этой цепи (рис.3.20).
 |
Таким образом, y u = y i + j и мгновенное напряжение на зажимах цепи записывается так:
 ,
| (3.71) |
а так как в данном случае y i= 0, то y u = j.
Рассмотрим треугольник напряжений на векторной диаграмме (рис.3.21).
Запишем выражения сторон треугольника:
  ,
 ,
 ,
| (3.72) (3.73) (3.74) |
где r – активное сопротивление катушки, Ом;
x L – реактивное сопротивление катушки, Ом;
– полное сопротивление катушки
(вводим такое понятие по аналогии с r и х L), Ом.
Разделим стороны треугольника напряжений на I m и получим треугольник
сопротивлений (рис.3.22).
|
|
Как видно из рисунка, полное сопротивление цепи катушки переменному току
  .
| (3.75) |
Угол сдвига фаз в катушке может быть найден через параметры катушки
(r, x L, ), например:
 .
| (3.76) |
Умножим стороны треугольника сопротивлений на квадрат действующего
значения тока и получим треугольник мощностей (рис.3.23).
Стороны треугольника представляют собой мощности:
| активную P = rI 2, Вт; | (3.76) |
| реактивную Q L = x L I 2, вар; | (3.77) |
| полную S = I 2, ва.
| (3.78) |
Введём понятие коэффициента мощности, под которым будем понимать
отношение активной мощности к полной 
.
Как видно из треугольника мощностей, коэффициент мощности численно равен косинусу угла сдвига фаз, т.е.
 .
| (3.79) |
Таким образом, реальную катушку можно рассматривать одновременно как
резистор – с одной стороны и как идеальную катушку – с другой. Все процессы можно описать с помощью двух идеальных элементов – активного сопротивления и индуктивности, описанные в п.3.2 и 3.3.
Пример 3.9
К реальной катушке подведено напряжение u = 282 sin (wt +70°) В.
Активное сопротивление катушки равно 3 Ом.
Реактивное сопротивление катушки равно 4 Ом.
Выполнить анализ цепи.
Решение.
1. Определяем полное сопротивление цепи по (3.75):
.
2. Определяем амплитуду тока по (3.74):
.
3. Определяем угол сдвига фаз цепи по (3.76):
.
4. Определяем начальную фазу тока:
y i = y u – j = 70 – 53 = 17°.
5. Записываем мгновенный ток:
i = 56,4 sin (wt +17°) А.
6. Определяем амплитуду напряжения на активном сопротивлении по (3.72):
U rm = 3×56,4 = 169,2 В.
7. Определяем начальную фазу напряжения на активном сопротивлении:
y ur = y i= 17°.
|
|
8. Записываем мгновенное напряжение на активном сопротивлении:
u r = 169,2 sin (wt +17°) В.
9. Определяем амплитуду напряжения на индуктивном сопротивлении по (3.73):
U Lm = 4×56,4 = 225,6 В.
10. Определяем начальную фазу напряжения на индуктивном сопротивлении:
y uL = y i+ 90 = 17 + 90 = 107°.
11. Записываем мгновенное напряжение на индуктивном сопротивлении:
u L = 225,6 sin (wt +107°) В.
12. Определяем действующее значение тока по (3.14):
.
13. Определяем активную мощность по (3.76):
Р = 3×402 = 4800 Вт = 4,8 кВт.
14. Определяем реактивную мощность по (3.77):
Q L = 4×402 = 6400 вар = 6,4 квар.
15. Определяем полную мощность по (3.78):
S = 5×402 = 8000 ва = 8,0 ква.
16. Определяем коэффициент мощности катушки по (3.79):
.
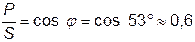Вопросы для самоконтроля
1. Опишите физические явления, наблюдаемые в реальной катушке
в цепи переменного синусоидального тока.
2. Составьте расчётную схему цепи с идеальным генератором и реальной катушкой.
3. Составьте уравнение электрического равновесия цепи синусоидального тока
с реальной катушкой.
4. Запишите выражение мгновенного тока в цепи, приняв начальную фазу равной нулю.
5. Получите выражение мгновенного напряжения на зажимах цепи, подставив
в уравнение электрического равновесия выражение мгновенного тока в цепи.
6. Постройте векторную диаграмму тока и напряжений цепи
(для действующих значений).
7. Запишите выражение мгновенного напряжения на зажимах цепи,
используя векторную диаграмму, с учётом угла сдвига фаз.
8. Получите из векторной диаграммы и постройте треугольник
действующих значений напряжений катушки.
9. Преобразуйте треугольник напряжений в треугольник сопротивлений,
используя закон Ома.
|
|
10. Установите связь между параметрами реальной катушки,
используя треугольник сопротивлений.
11. Как рассчитать угол сдвига фаз реальной катушки с помощью её параметров?
12. Получите из треугольника сопротивлений треугольник мощностей и постройте его.
13. Установите связь между мощностями реальной катушки,
используя треугольник мощностей.
14. Дайте определение коэффициента мощности реальной катушки.
15. Запишите и расшифруйте определяющую формулу коэффициента мощности
реальной катушки.
Задания для самоконтроля
Катушка с параметрами r = 3 Ом и L = 12,7 мГн подключена
к источнику синусоидального напряжения u = 282(wt + 70°) В.
Частота тока в цепи f = 50 Гц.
1. Найти индуктивное сопротивление катушки.
2. Найти полное сопротивление катушки.
3. Найти угол сдвига фаз катушки.
4. Найти амплитуду тока в катушке.
5. Записать мгновенное значение тока в катушке.
6. Найти амплитуду напряжения на активном сопротивлении
7. Записать мгновенное значение напряжения на активном сопротивлении.
8. Найти амплитуду напряжения на индуктивности.
9. Записать мгновенное значение напряжения на индуктивности.
10. Построить векторную диаграмму напряжений и тока цепи.
11. Найти активную мощность катушки.
12. Найти реактивную мощность катушки.
13. Найти полную мощность катушки.
14. Найти коэффициент мощности катушки.