Расчет среднеповерхностной температуры нагретой зоны герметичной РЭА.

 

1. Краткая теория

Пусть РЭА имеет герметичный корпус в форме прямоугольного параллелепипеда, внутри которого расположено горизонтальное шасси.

Шасси вместе с расположенным на нем деталями представляет собой нагретую зону. Очевидно, анализ нагретых зон в общем случае является громоздким, так как зона содержит детали разных размеров и конфигураций. Для упрощения анализа примем следующие допущения:

1) расстояние между соседними деталями мало ив узких зазорах образуются зоны застойного воздуха;

2) излучение поверхностей радиодеталей и шасси, расположенных “в глубине” нагретой зоны, экранируется соседними деталями и практически не достигает корпуса РЭА;

3) кондуктивные связи “шасси-корпус” слабо влияют на тепловой режим нагретой зоны.

Приведенные допущения подтверждаются опытным путем для современной РЭА, которая характеризуется большой плотностью монтажа.

Представим нагретую зону в виде параллелепипеда, который называется эквивалентной нагретой зоной (рис. 1). Размеры эквивалентной нагретой зоны определяют из факта, установленного опытным путем: объем реальной нагретой зоны и объем эквивалентной зоны должны совпадать. Ширина и длина эквивалентной зоны совпадают с внутренними размерами корпуса. Следовательно,

; ;

где - длина, ширина и высота эквивалентной зоны;

- длина и ширина корпуса РЭА;

- толщина стенок корпуса.

Представим

где - внутренняя высота корпуса;

- внутренний объем аппарата.

Величина называется коэффициентом заполнения РЭА.

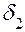Зазоры и определяются по очевидным формулам (см. рис. 1)

,

где - объем деталей над (под) шасси.

По предположению, зазор .

Представим РЭА в виде системы тел, состоящей из оболочки (корпус РЭА), тела (эквивалентная нагретая зона) и среды (воздух, заполняющий свободный объем корпуса). Тепловая схема для изучаемой системы тел приведена на рис. 2,

где

- проводимость “зона-корпус”, обусловленная излучением;

- проводимость “зона-корпус”, обусловленная конвекцией над нагретой зоной (область 1);

- проводимость “зона-корпус”, обусловленная кондукцией под нагретой зоной (область 2);

- проводимость “зона-корпус”, обусловленная конвекцией в области 3.

Проводимость определяется по формуле

,

где - площадь эквивалентной нагретой зоны;

- радиационный коэффициент теплоотдачи.

Аналогичным образом

; ;

где 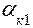- определяется по эмпирической формуле

описывающей конвекцию в ограниченном пространстве при условии, что нагретая сторона расположена снизу.

Поскольку в области 2 движение воздуха отсутствует (нагретая сторона расположена сверху), то

где - теплопроводность воздуха при температуре

В области 3 движение воздуха имеет смешанный характер. Опытным путем установлено, что

Поскольку проводимости , , , зависят от температуры, то уравнение, описывающее тепловую схему (рис. 2), является нелинейным. Рассмотрим определения , основанные на методе последовательных приближений.

 

2. Алгоритм

Исходные данные:

- размеры нагретой зоны ;

- зазоры и ;

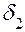- степени черноты зоны и корпуса ;

- температуры корпуса и среды ;

- мощность, выделяющаяся в нагретой зоне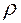

1. Определить начальное приближение температуры зоны

(формула получена опытным путем).

2. Определить площади

;

;

.

3. Вычислить проводимость :

a. Коэффициент теплоотдачи

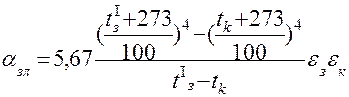
b. Проводимость .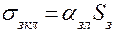

4. Определить проводимость

a. Коэффициент теплоотдачи

,

где определяется по табл. 1 при

b. Проводимость

5. Определить проводимость

a. Коэффициент теплоотдачи ,

где - определяется по табл. 2 при .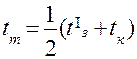

Таблица 1. Значение для воздуха

, 0С
	0,63	0,58	0,56

 

Таблица 2. Значение для воздуха

, 0С
	0,026	0,0268	0,0276	0,0283	0,029	0,0297	0,0305	0,0313	0,0321	0,0329

 

b. Проводимость .

6. Вычислить проводимость

a. Коэффициент теплоотдачи

b. Проводимость .

7. Определить проводимость “зона-корпус”

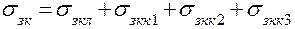
8. Вычислить следующие приближение температуры зоны:

9.Если , то конец. В противном случае принять за исходную температуру зоны, т.е. 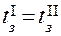и перейти к п.3.

 

3. Пример

Вычислить температуру эквивалентной нагретой зоны РЭА, характеризуемой следующими параметрами:

 

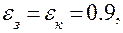
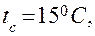
1. Температура зоны в первом приближении

2. Площади

;

;

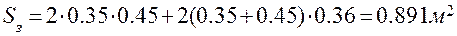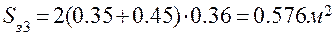
3.1. Коэффициент теплоотдачи

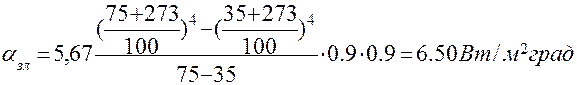
3.2. Проводимость

4.1. Коэффициент теплоотдачи

4.2. Проводимость

5.1. Коэффициент теплоотдачи

5.2. Проводимость

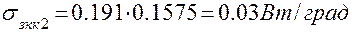
6.1. Коэффициент теплоотдачи

6.2. Проводимость

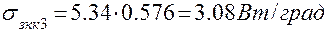
7. Проводимость “зона-корпус”

8. Следующее приближение температуры зоны

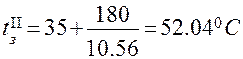
9. Поскольку , то устанавливаем , переходим к п.3.1.

Повторный расчет дает .

Следовательно, температура нагретой зоны равна .

 

Контрольное задание

Вычислить среднеповерхностную температуру эквивалентной нагретой зоны РЭА, размеры которой приведены в табл. 3. Зазоры и .

Степени черноты мощность 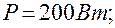температура корпуса температура среды

Таблица 3

Вариант
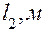
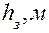
	0.3	0.3	0.3
	0.3	0.3	0.4
	0.3	0.3	0.5
	0.3	0.4	0.3
	0.3	0.4	0.4
	0.3	0.4	0.5
	0.3	0.5	0.3
	0.3	0.5	0.4
	0.3	0.5	0.5
	0.4	0.3	0.3
	0.4	0.3	0.4
	0.4	0.3	0.5
	0.4	0.4	0.3
	0.4	0.4	0.4
	0.4	0.4	0.5
	0.4	0.5	0.3
	0.4	0.5	0.4
	0.4	0.5	0.5
	0.5	0.3	0.3
	0.5	0.3	0.4
	0.5	0.3	0.5
	0.5	0.4	0.3
	0.5	0.4	0.4
	0.5	0.4	0.5
	0.5	0.5	0.3
	0.5	0.5	0.4
	0.5	0.5	0.5