Нахождение компонент связности
| 9. Связность в ориентированных графах. Компонента сильной связности и её свойства. Нахождение компонент сильной связности. Сеть. Конденсат орграфа. Примеры.
Связность в орграфах
 Если начальная вершина совпадает с конечной, то такой маршрут называется контуром. Две вершины
Если начальная вершина совпадает с конечной, то такой маршрут называется контуром. Две вершины  и и 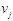 сильно связны, если существует маршрут сильно связны, если существует маршрут 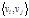 и существует маршрут и существует маршрут  . .
 Орграф называется сильно связным, если любые две его вершины сильно связны.
Пример
Орграф называется сильно связным, если любые две его вершины сильно связны.
Пример
 Максимальный по включению вершин подграф орграфа, любые две вершины которого сильно связны, называется компонентой сильной связности орграфа (КСС).
Отношение сильной связности является отношением эквивалентности на множестве вершин. Таким образом разбиение орграфа на КСС – это разбиение множества вершин на классы эквивалентности.
Нахождение КСС
Теорема Любая вершина орграфа принадлежит ровно одной КСС орграфа.
Максимальный по включению вершин подграф орграфа, любые две вершины которого сильно связны, называется компонентой сильной связности орграфа (КСС).
Отношение сильной связности является отношением эквивалентности на множестве вершин. Таким образом разбиение орграфа на КСС – это разбиение множества вершин на классы эквивалентности.
Нахождение КСС
Теорема Любая вершина орграфа принадлежит ровно одной КСС орграфа. 
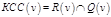 , где , где 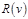 - множество вершин, достижимых из - множество вершин, достижимых из 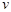 , , 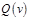 - множество вершин, из которых достижимо - множество вершин, из которых достижимо 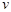 . .

  Орграф, в котором отсутствуют контуры, называется сетью. В сети есть следующие особые элементы:
Каждая вершина в сети является компонентой сильной связности. Пусть
Орграф, в котором отсутствуют контуры, называется сетью. В сети есть следующие особые элементы:
Каждая вершина в сети является компонентой сильной связности. Пусть  - орграф и - орграф и 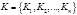 - его КСС. Конденсатом орграфа - его КСС. Конденсатом орграфа  называется сеть, которая получена из орграфа путем сжатия каждой КСС в одну вершину. называется сеть, которая получена из орграфа путем сжатия каждой КСС в одну вершину.
 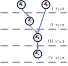
|
10.Вершинно и реберно непересекающиеся цепи. Разделяющее множество. Теорема Менгера.
Пусть 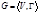 -некоторый граф, и -некоторый граф, и 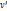 и и  –две его несмежные вершины.
Две цепи –две его несмежные вершины.
Две цепи 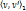 и и  называются вершинно-непересекающимися, если у них нет общих вершин за исключением концевых.
Две цепи называются вершинно-непересекающимися, если у них нет общих вершин за исключением концевых.
Две цепи 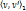 и и  называются реберно-непересекающимися, если у них нет общих ребер.
Если две цепи называются реберно-непересекающимися, если у них нет общих ребер.
Если две цепи 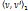 и и  - вершинно непересекающиеся, то они и реберно непересекающиеся.
Пусть - вершинно непересекающиеся, то они и реберно непересекающиеся.
Пусть 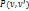 -множество вершинно-непересекающихся цепей -множество вершинно-непересекающихся цепей 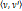 Множество
Множество  вершин графа разделяет две вершины вершин графа разделяет две вершины 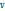 и и 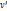 , если , если 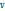 и и 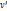 принадлежат разным компонентам связности графа G-S
Теорема Менгера
Пусть принадлежат разным компонентам связности графа G-S
Теорема Менгера
Пусть 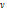 и и 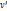 - несмежные вершины в графе G. Наименьшее число вершин в множестве, разделяющем - несмежные вершины в графе G. Наименьшее число вершин в множестве, разделяющем 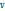 и и 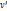 , равно наибольшему числу вершинно-непересекающихся простых , равно наибольшему числу вершинно-непересекающихся простых 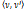 цепей: цепей:

| 11.Понятие цикла в графе. Эйлеров и гамильтонов циклы. Эйлеров граф. Гамильтонов граф. Критерий эйлеровости графа. Примеры.
Цикл в графе называется Эйлеровым, если любое ребро графа участвует в его образовании ровно один раз. Граф, содержащий Эйлеров цикл называется Эйлеровым.
Теорема Эйлера Граф является Эйлеровым тогда и только тогда, когда степени всех его вершин четные.
Цикл в графе называется Гамильтоновым, если каждая вершина графа участвует в его образовании ровно один раз. Граф, содержащий Гамильтонов цикл называется Гамильтоновым.
Свойства «Эйлеровости» и «Гамильтоновости» являются независимыми.
| 12.Цикломатика графов: цикл как вектор, пространство циклов графа, цикломатическая матрица, цикломатический базис, цикломатическое число. Алгоритм порождения базисной системы циклов. Нахождение всех циклов графа. Критерий двудольности графа (теорема Кёнига). Пример.
Пусть  - граф. Цикл в графе может быть записан в виде - граф. Цикл в графе может быть записан в виде 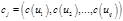 , где , где 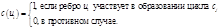 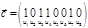 Каждый цикл может быть представлен в качестве двоичного вектора. Множество циклов образует пространство двоичных векторов. Цикломатический базис – совокупность линейно независимых циклов графа, с помощью которых могут быть получены все остальные циклы. Цикломатическое число графа
Каждый цикл может быть представлен в качестве двоичного вектора. Множество циклов образует пространство двоичных векторов. Цикломатический базис – совокупность линейно независимых циклов графа, с помощью которых могут быть получены все остальные циклы. Цикломатическое число графа  -мощность базисной системы циклов графа -мощность базисной системы циклов графа 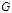 . .  Граф, у которого цикломатическое число равно 0, называется деревом (или ациклическим графом). Многокомпонентный ациклический граф называется деревом. Остов графа – частичный граф исходного графа, в котором число вершин и число компонент связности совпадает с числом вершин и числом компонент связности исходного графа, но цикломатическое число равно 0.
Алгоритм нахождения базисной системы циклов
1. Получить остов графа (удалить
Граф, у которого цикломатическое число равно 0, называется деревом (или ациклическим графом). Многокомпонентный ациклический граф называется деревом. Остов графа – частичный граф исходного графа, в котором число вершин и число компонент связности совпадает с числом вершин и числом компонент связности исходного графа, но цикломатическое число равно 0.
Алгоритм нахождения базисной системы циклов
1. Получить остов графа (удалить  ребер; удаляемые ребра называются хордами). 2. Добавляя к остову поочередно по одной хорде получаем базисную систему циклов.
Число циклов в графе не превосходит ребер; удаляемые ребра называются хордами). 2. Добавляя к остову поочередно по одной хорде получаем базисную систему циклов.
Число циклов в графе не превосходит  .
Теорема Кенига Граф двудолен тогда и только тогда, когда он не содержит циклов нечетной длины. .
Теорема Кенига Граф двудолен тогда и только тогда, когда он не содержит циклов нечетной длины.
|
13.Разделяющее множество вершин и разрез (коцикл) графа. Коциклический ранг графа. Поиск базисной системы разрезов в графе. Пример.
Пусть  - некоторый связный граф. Подмножество ребер графа называется разделяющим множеством, если удаление их из графа изменяет число компонент связности. Разделяющее множество называется разрезом графа, если любое его собственно подмножество не является разделяющим.
Пример - некоторый связный граф. Подмножество ребер графа называется разделяющим множеством, если удаление их из графа изменяет число компонент связности. Разделяющее множество называется разрезом графа, если любое его собственно подмножество не является разделяющим.
Пример
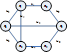
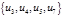 - разделяющее множество, разрез.
цикл - разделяющее множество, разрез.
цикл  разрез (коцикл)
Коциклический ранг разрез (коцикл)
Коциклический ранг 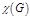 - число линейно независимых коциклов графа. - число линейно независимых коциклов графа. 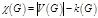 .
Пример .
Пример
  .
Алгоритм нахождения базисной системы разрезов
1. Построить остов графа .
Алгоритм нахождения базисной системы разрезов
1. Построить остов графа  . 2. Удалять поочередно по одному ребру (остов распадается на две компоненты). Добавить к разрезу те хорды, концы которых принадлежат разным компонентам. . 2. Удалять поочередно по одному ребру (остов распадается на две компоненты). Добавить к разрезу те хорды, концы которых принадлежат разным компонентам.
| 14.Внешняя устойчивость графа. Число внешней устойчивости графа. Положительная и отрицательная внешняя устойчивость орграфов. Пример.
Внешняя устойчивость графа
Пусть 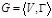 - некоторый граф. Подмножество вершин - некоторый граф. Подмножество вершин  называется множеством внешней устойчивости, если 1) называется множеством внешней устойчивости, если 1) 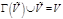 2) 2) 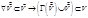 Мощность минимального множества внешней устойчивости называется числом внешней устойчивости графа
Мощность минимального множества внешней устойчивости называется числом внешней устойчивости графа 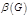 . Для того, чтобы найти все множества внешней устойчивости графа, надо найти все покрытия модифицированной матрицы смежности графа. Модификация заключается в добавлении единичной главной диагонали.
Внешняя устойчивость орграфа . Для того, чтобы найти все множества внешней устойчивости графа, надо найти все покрытия модифицированной матрицы смежности графа. Модификация заключается в добавлении единичной главной диагонали.
Внешняя устойчивость орграфа
 есть множество положительной внешней устойчивости орграфа есть множество положительной внешней устойчивости орграфа  , если 1) , если 1) 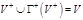 2) 2) 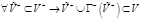 . Число положительной внешней устойчивости орграфа – мощность минимального множества положительной внешней устойчивости . Число положительной внешней устойчивости орграфа – мощность минимального множества положительной внешней устойчивости 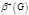
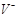 есть множество отрицательной внешней устойчивости орграфа есть множество отрицательной внешней устойчивости орграфа  , если 1) , если 1)  2) 2) 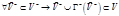 Число отрицательной внешней устойчивости орграфа – мощность минимального множества отрицательной внешней устойчивости Число отрицательной внешней устойчивости орграфа – мощность минимального множества отрицательной внешней устойчивости  .
Поиск множеств положительной (отрицательной) внешней устойчивости орграфа производится по модифицированной матрице смежности (модификация заключается в добавлении единичной главной диагонали) с помощью покрытия. При этом покрытия столбцов строками порождают все множества положительной внешней устойчивости, а покрытия всех строк столбцами порождают все множества отрицательной внешней устойчивости. .
Поиск множеств положительной (отрицательной) внешней устойчивости орграфа производится по модифицированной матрице смежности (модификация заключается в добавлении единичной главной диагонали) с помощью покрытия. При этом покрытия столбцов строками порождают все множества положительной внешней устойчивости, а покрытия всех строк столбцами порождают все множества отрицательной внешней устойчивости.
| 15.Внутренняя устойчивость графа. Пустой подграф. Число внутренней устойчивости. Алгоритм порождения пустых подграфов. Пример.
Подмножество вершин графа называется внутренне устойчивым, если они попарно несмежны между собой. Внутренне устойчивое множество вершин называется пустым подграфом, если при добавлении хотя бы одной вершины свойство внутренней устойчивости пропадает. Мощность максимального пустого подграфа называется числом внутренней устойчивости графа 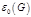 .
Пусть .
Пусть  - некоторый граф, - некоторый граф,  - некоторая вершина, - некоторая вершина, 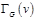 - окрестность вершины - окрестность вершины  . Неокрестность (коокрестность) вершины . Неокрестность (коокрестность) вершины  графа графа 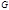 обозначим обозначим 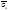 - подграф графа - подграф графа  , порожденный , порожденный 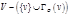 .
Теорема Пустой подграф, содержащий вершину .
Теорема Пустой подграф, содержащий вершину 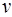 содержит по крайней мере одну вершину из коокрестности вершины содержит по крайней мере одну вершину из коокрестности вершины  .
Алгоритм нахождения пустых подграфов
Начальный шаг: строится вершина – корень дерева, которой сопоставляется граф .
Алгоритм нахождения пустых подграфов
Начальный шаг: строится вершина – корень дерева, которой сопоставляется граф  . Итерационный шаг: на . Итерационный шаг: на 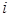 -ом ярусе есть вершина, которой сопоставлен граф -ом ярусе есть вершина, которой сопоставлен граф 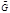 . а) Из . а) Из  выбирается любая вершина выбирается любая вершина  и выносится на и выносится на  ярус. б) На ярус. б) На  ярус выносятся все вершины, которые входят в ярус выносятся все вершины, которые входят в 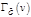 . в) Каждая из вершин . в) Каждая из вершин 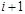 яруса взвешивается соответствующим графом – коокрестностью от графа яруса взвешивается соответствующим графом – коокрестностью от графа  . Заключительный шаг: вершина дерева будет висячей, если соответствующий ей граф – пустой граф. Замечание В пункте а) желательно выбирать ту вершину, которая имеет минимальную степень. . Заключительный шаг: вершина дерева будет висячей, если соответствующий ей граф – пустой граф. Замечание В пункте а) желательно выбирать ту вершину, которая имеет минимальную степень.
|
16.Полный граф. Полные подграфы. Плотность графа. Алгоритм порождения полных подграфов. Пример.
Пусть 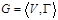 - некоторый граф. Максимальный по включению вершин подграф графа, любые две вершины которого смежны называется полным подграфом. Мощность максимального полного подграфа называется плотностью графа - некоторый граф. Максимальный по включению вершин подграф графа, любые две вершины которого смежны называется полным подграфом. Мощность максимального полного подграфа называется плотностью графа 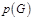 .
Алгоритм нахождения полных подграфов
Начальный шаг: строится вершина – корень дерева, которой сопоставляется граф .
Алгоритм нахождения полных подграфов
Начальный шаг: строится вершина – корень дерева, которой сопоставляется граф 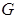 . Итерационный шаг: на . Итерационный шаг: на 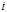 -ом ярусе есть вершина, которой сопоставлен граф -ом ярусе есть вершина, которой сопоставлен граф 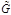 . а) Из . а) Из  выбирается любая вершина выбирается любая вершина 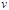 и выносится на и выносится на  ярус. б) На ярус. б) На  ярус выносятся все вершины, которые входят в ярус выносятся все вершины, которые входят в 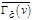 . в) Каждая из вершин . в) Каждая из вершин  яруса взвешивается соответствующим графом – окрестностью от графа яруса взвешивается соответствующим графом – окрестностью от графа 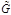 . Заключительный шаг: вершина дерева будет висячей, если соответствующий ей граф – пустой граф. Замечание В пункте а) желательно выбирать ту вершину, которая имеет максимальную степень.
Задачу нахождения полных подграфов в . Заключительный шаг: вершина дерева будет висячей, если соответствующий ей граф – пустой граф. Замечание В пункте а) желательно выбирать ту вершину, которая имеет максимальную степень.
Задачу нахождения полных подграфов в 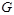 можно свести к задаче нахождения пустых подграфов в можно свести к задаче нахождения пустых подграфов в  . .
| 17. Рёберные графы. Свойство реберности. Критерий рёберности. Нахождения образа рёберного графа. Пример.
Пусть 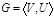 - некоторый граф. Назовем граф - некоторый граф. Назовем граф  реберным графом реберным графом 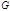 , если носитель графа , если носитель графа  совпадает с множеством ребер графа совпадает с множеством ребер графа 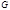 , и две вершины в , и две вершины в  смежны, если соответствующие ребра смежны в смежны, если соответствующие ребра смежны в 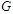 .
Пример .
Пример
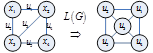 (это преобразование можно выполнить
всегда)
(это преобразование можно выполнить
всегда)
| Граф  обладает свойством реберности, если существует некоторый граф, реберный для которого является изоморфным для обладает свойством реберности, если существует некоторый граф, реберный для которого является изоморфным для 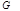 . .
Пример
Теорема
Граф 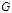 обладает свойством реберности, если существует разложение ребер графа на полные подграфы такое, что каждая вершина графа принадлежит не более чем двум полным подграфам. обладает свойством реберности, если существует разложение ребер графа на полные подграфы такое, что каждая вершина графа принадлежит не более чем двум полным подграфам.
Замечание
1. Не для любого графа существует такое разложение ребер.
2. В разложении ребер каждое ребро принадлежит ровно одному подграфу.
Если граф обладает свойством реберности, то как найти его образ (т.е. граф, для которого данный является реберным)?
| 18.Род поверхности и род графа. Укладка графа на поверхности. Планарные графы. Критерий планарности.
Укладки графа. Планарность
Исследуются топологические свойства графа. Гомеоморфизм графов – еще одно отношение эквивалентности на графах. Два графа 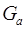 и и 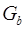 гомеоморфны, если они изоморфны с точностью до цепей степени 2.
Пусть гомеоморфны, если они изоморфны с точностью до цепей степени 2.
Пусть 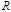 - некоторая поверхность. Род поверхности - некоторая поверхность. Род поверхности 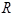 - это максимальное число простых замкнутых кривых, не разделяющих эту поверхность.
Род графа - это максимальное число простых замкнутых кривых, не разделяющих эту поверхность.
Род графа 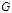 - - 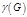 - минимальный род поверхности, на которой можно «уложить» граф - минимальный род поверхности, на которой можно «уложить» граф 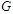 без взаимных пересечений ребер (ребра пересекаются только в вершинах).
Граф без взаимных пересечений ребер (ребра пересекаются только в вершинах).
Граф  называется планарным(плоским), если называется планарным(плоским), если 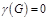 .
печатные платы – планарные графы;
микросхемы (на уровне технологии их изготовления) – планарные графы.
Критерий планарности графа (критерий Понтрягина-Куратовского)
Граф планарен тогда и только тогда, когда в нем отсутствуют подграфы, гомеоморфные .
печатные платы – планарные графы;
микросхемы (на уровне технологии их изготовления) – планарные графы.
Критерий планарности графа (критерий Понтрягина-Куратовского)
Граф планарен тогда и только тогда, когда в нем отсутствуют подграфы, гомеоморфные 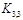 или или 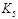 .
Алгоритм приведения графа .
Алгоритм приведения графа 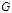 к планарному
1) Найти все подграф, гомеоморфные к планарному
1) Найти все подграф, гомеоморфные 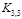 и и 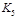 . 2) Построить таблицу покрытия найденных в п.1 подграфов ребрами, которые их образуют. 3) Найти минимальное покрытие подграфов ребрами (удалив ребра, образующие покрытие, получим планарный граф). . 2) Построить таблицу покрытия найденных в п.1 подграфов ребрами, которые их образуют. 3) Найти минимальное покрытие подграфов ребрами (удалив ребра, образующие покрытие, получим планарный граф).
|
19.Раскраска графа. Хроматическое число. Алгоритм нахождения хроматического числа и раскраски графа. Хроматическое число для базовых типов графов. Пример.
Пусть  - некоторый граф и - некоторый граф и  - разбиение - разбиение  на на 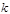 внутренне устойчивых множеств. В этом случае говорят, что вершины графа допускают раскраску в внутренне устойчивых множеств. В этом случае говорят, что вершины графа допускают раскраску в 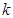 цветов (цвета по номерам цветов (цвета по номерам  ). Хроматическое число ). Хроматическое число 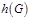 - минимальное значение - минимальное значение  , которое допускает раскраску графа.
Хроматическое число пустого графа равно 1. Хроматическое число , которое допускает раскраску графа.
Хроматическое число пустого графа равно 1. Хроматическое число 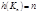 . Хроматическое число . Хроматическое число 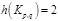 .
Алгоритм нахождения раскраски (хроматического числа)
1) Выделить все пустые подграфы графа. 2) Построить таблицу покрытий вершин графа пустыми подграфами. 3) Найти минимальное покрытие вершин графа пустыми подграфами (мощность минимального покрытия – это .
Алгоритм нахождения раскраски (хроматического числа)
1) Выделить все пустые подграфы графа. 2) Построить таблицу покрытий вершин графа пустыми подграфами. 3) Найти минимальное покрытие вершин графа пустыми подграфами (мощность минимального покрытия – это 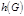 , а само покрытие определяет раскраску). , а само покрытие определяет раскраску).
| 20.Оценки хроматического числа. Приближенная оценка (раскраска) по Ершову. Значение (оценка) хроматического числа для операций над графам.
Оценки хроматического числа
1. Теорема Кенига Граф бихроматичен ( ) тогда и только тогда, когда в ) тогда и только тогда, когда в 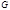 нет циклов нечетной длины.
2. Теорема нет циклов нечетной длины.
2. Теорема  , где , где 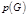 - плотность графа - плотность графа 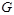 .
3. Теорема .
3. Теорема 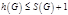 , где , где 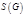 - степень графа - степень графа 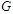 .
4. Оценка Бержа .
4. Оценка Бержа  , где , где 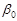 - число внешней устойчивости графа - число внешней устойчивости графа  .
5.
Теорема .
5.
Теорема  , где , где  , ,  . . 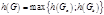 , где , где 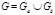 , , 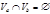 . . 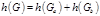 , где , где  , , 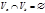 . . 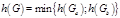 , где , где  .
Алгоритм приближенной раскраски графа (алгоритм Ершова)
Алгоритм основан на стягивании несмежных вершин: .
Алгоритм приближенной раскраски графа (алгоритм Ершова)
Алгоритм основан на стягивании несмежных вершин:
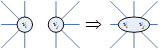
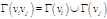 Стягивание проводить до тех пор, пока не получим полный граф. Мощность этого полного графа является оценкой хроматического числа сверху, а сам полный граф определяет приближенную раскраску графа.
Замечание В первую очередь желательно стягивать те вершины, расстояние между которыми четно.
Стягивание проводить до тех пор, пока не получим полный граф. Мощность этого полного графа является оценкой хроматического числа сверху, а сам полный граф определяет приближенную раскраску графа.
Замечание В первую очередь желательно стягивать те вершины, расстояние между которыми четно.
| 21.Группа подстановок. Свойства группы. Вычисление произведения подстановок.
Группа – алгебра с одно бинарной операцией (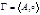 ), которая обладает следующими свойствами:
1) замкнутость ), которая обладает следующими свойствами:
1) замкнутость 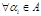 и и 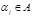 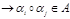 2) ассоциативность 2) ассоциативность 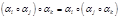 3) наличие нейтрального элемента 3) наличие нейтрального элемента 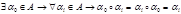 4) существование обратного элемента для 4) существование обратного элемента для 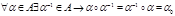 Группа подстановки. Пусть
Группа подстановки. Пусть 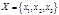 . Подстановкой назовем . Подстановкой назовем 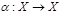 . .
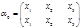 
  Операция: произведение подстановок
Операция: произведение подстановок 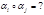 

|
22.Автоморфизм и группа автоморфизмов графа.
Пусть  - некоторый граф. Автоморфизм графа - некоторый граф. Автоморфизм графа  - это изоморфизм на себя (с, сохраняющая отношение смежности между вершинами графа).
Пример - это изоморфизм на себя (с, сохраняющая отношение смежности между вершинами графа).
Пример
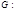 
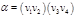 - не является автоморфизмом. - не является автоморфизмом. 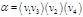 - автоморфизм.
Группа автоморфизмов графа - автоморфизм.
Группа автоморфизмов графа 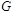 - - 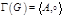 , где , где  - множество всех автоморфизмов графа, - множество всех автоморфизмов графа, 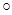 - операция произведения.
Пример - операция произведения.
Пример
| 23.Операции на группах автоморфизмов. Сложение и произведение групп автоморфизмов.
Операции над группами
Пусть даны группы автоморфизмов 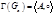 , , 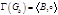 . . 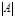 - порядок группы - порядок группы  , , 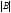 - порядок группы - порядок группы  . Группа . Группа  действует на множестве действует на множестве 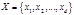 . Группа . Группа  действует на множестве действует на множестве 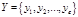 ( (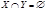 ). ). 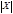 - степень группы - степень группы  . .  - степень группы - степень группы 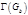 . Рассмотрим три операции над группами:
Сложение (объединение) групп – « . Рассмотрим три операции над группами:
Сложение (объединение) групп – «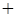 ».
Умножение групп – « ».
Умножение групп – «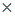 ». ».
Сложение групп.

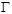 действует на действует на 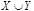
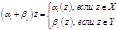
Степень 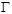 равна равна  , порядок , порядок  равен равен 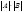
Произведение групп
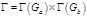
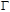 действует на действует на 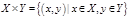
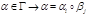

Степень 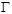 равна равна 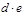 , порядок , порядок 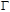 равен равен 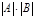 . .
|
|
 в список.
в список. ).
).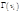 и добавить в список те вершины из окрестности, которых нет в списке.
и добавить в список те вершины из окрестности, которых нет в списке. как просмотренную.
как просмотренную. Если начальная вершина совпадает с конечной, то такой маршрут называется контуром. Две вершины
Если начальная вершина совпадает с конечной, то такой маршрут называется контуром. Две вершины  и
и 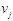 сильно связны, если существует маршрут
сильно связны, если существует маршрут 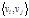 и существует маршрут
и существует маршрут  .
.
 Орграф называется сильно связным, если любые две его вершины сильно связны.
Пример
Орграф называется сильно связным, если любые две его вершины сильно связны.
Пример
 Максимальный по включению вершин подграф орграфа, любые две вершины которого сильно связны, называется компонентой сильной связности орграфа (КСС).
Отношение сильной связности является отношением эквивалентности на множестве вершин. Таким образом разбиение орграфа на КСС – это разбиение множества вершин на классы эквивалентности.
Нахождение КСС
Теорема Любая вершина орграфа принадлежит ровно одной КСС орграфа.
Максимальный по включению вершин подграф орграфа, любые две вершины которого сильно связны, называется компонентой сильной связности орграфа (КСС).
Отношение сильной связности является отношением эквивалентности на множестве вершин. Таким образом разбиение орграфа на КСС – это разбиение множества вершин на классы эквивалентности.
Нахождение КСС
Теорема Любая вершина орграфа принадлежит ровно одной КСС орграфа. 
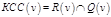 , где
, где 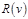 - множество вершин, достижимых из
- множество вершин, достижимых из 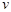 ,
, 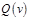 - множество вершин, из которых достижимо
- множество вершин, из которых достижимо 

 Орграф, в котором отсутствуют контуры, называется сетью. В сети есть следующие особые элементы:
Каждая вершина в сети является компонентой сильной связности. Пусть
Орграф, в котором отсутствуют контуры, называется сетью. В сети есть следующие особые элементы:
Каждая вершина в сети является компонентой сильной связности. Пусть  - орграф и
- орграф и 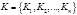 - его КСС. Конденсатом орграфа
- его КСС. Конденсатом орграфа  называется сеть, которая получена из орграфа путем сжатия каждой КСС в одну вершину.
называется сеть, которая получена из орграфа путем сжатия каждой КСС в одну вершину.


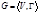 -некоторый граф, и
-некоторый граф, и 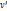 и
и  –две его несмежные вершины.
Две цепи
–две его несмежные вершины.
Две цепи 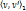 и
и  называются вершинно-непересекающимися, если у них нет общих вершин за исключением концевых.
Две цепи
называются вершинно-непересекающимися, если у них нет общих вершин за исключением концевых.
Две цепи 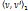 и
и 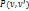 -множество вершинно-непересекающихся цепей
-множество вершинно-непересекающихся цепей 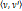 Множество
Множество  вершин графа разделяет две вершины
вершин графа разделяет две вершины 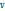 и
и 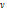 и
и 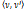 цепей:
цепей:

 - граф. Цикл в графе может быть записан в виде
- граф. Цикл в графе может быть записан в виде 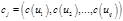 , где
, где 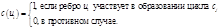
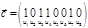 Каждый цикл может быть представлен в качестве двоичного вектора. Множество циклов образует пространство двоичных векторов. Цикломатический базис – совокупность линейно независимых циклов графа, с помощью которых могут быть получены все остальные циклы. Цикломатическое число графа
Каждый цикл может быть представлен в качестве двоичного вектора. Множество циклов образует пространство двоичных векторов. Цикломатический базис – совокупность линейно независимых циклов графа, с помощью которых могут быть получены все остальные циклы. Цикломатическое число графа  -мощность базисной системы циклов графа
-мощность базисной системы циклов графа 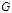 .
.  Граф, у которого цикломатическое число равно 0, называется деревом (или ациклическим графом). Многокомпонентный ациклический граф называется деревом. Остов графа – частичный граф исходного графа, в котором число вершин и число компонент связности совпадает с числом вершин и числом компонент связности исходного графа, но цикломатическое число равно 0.
Алгоритм нахождения базисной системы циклов
1. Получить остов графа (удалить
Граф, у которого цикломатическое число равно 0, называется деревом (или ациклическим графом). Многокомпонентный ациклический граф называется деревом. Остов графа – частичный граф исходного графа, в котором число вершин и число компонент связности совпадает с числом вершин и числом компонент связности исходного графа, но цикломатическое число равно 0.
Алгоритм нахождения базисной системы циклов
1. Получить остов графа (удалить  .
Теорема Кенига Граф двудолен тогда и только тогда, когда он не содержит циклов нечетной длины.
.
Теорема Кенига Граф двудолен тогда и только тогда, когда он не содержит циклов нечетной длины.
 - некоторый связный граф. Подмножество ребер графа называется разделяющим множеством, если удаление их из графа изменяет число компонент связности. Разделяющее множество называется разрезом графа, если любое его собственно подмножество не является разделяющим.
Пример
- некоторый связный граф. Подмножество ребер графа называется разделяющим множеством, если удаление их из графа изменяет число компонент связности. Разделяющее множество называется разрезом графа, если любое его собственно подмножество не является разделяющим.
Пример

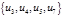 - разделяющее множество, разрез.
цикл
- разделяющее множество, разрез.
цикл  разрез (коцикл)
Коциклический ранг
разрез (коцикл)
Коциклический ранг 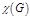 - число линейно независимых коциклов графа.
- число линейно независимых коциклов графа. 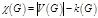 .
Пример
.
Пример

 .
Алгоритм нахождения базисной системы разрезов
1. Построить остов графа
.
Алгоритм нахождения базисной системы разрезов
1. Построить остов графа  . 2. Удалять поочередно по одному ребру (остов распадается на две компоненты). Добавить к разрезу те хорды, концы которых принадлежат разным компонентам.
. 2. Удалять поочередно по одному ребру (остов распадается на две компоненты). Добавить к разрезу те хорды, концы которых принадлежат разным компонентам.
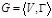 - некоторый граф. Подмножество вершин
- некоторый граф. Подмножество вершин  называется множеством внешней устойчивости, если 1)
называется множеством внешней устойчивости, если 1) 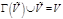 2)
2) 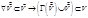 Мощность минимального множества внешней устойчивости называется числом внешней устойчивости графа
Мощность минимального множества внешней устойчивости называется числом внешней устойчивости графа 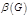 . Для того, чтобы найти все множества внешней устойчивости графа, надо найти все покрытия модифицированной матрицы смежности графа. Модификация заключается в добавлении единичной главной диагонали.
Внешняя устойчивость орграфа
. Для того, чтобы найти все множества внешней устойчивости графа, надо найти все покрытия модифицированной матрицы смежности графа. Модификация заключается в добавлении единичной главной диагонали.
Внешняя устойчивость орграфа
 есть множество положительной внешней устойчивости орграфа
есть множество положительной внешней устойчивости орграфа 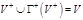 2)
2) 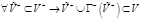 . Число положительной внешней устойчивости орграфа – мощность минимального множества положительной внешней устойчивости
. Число положительной внешней устойчивости орграфа – мощность минимального множества положительной внешней устойчивости 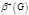
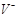 есть множество отрицательной внешней устойчивости орграфа
есть множество отрицательной внешней устойчивости орграфа  , если 1)
, если 1)  2)
2) 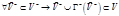 Число отрицательной внешней устойчивости орграфа – мощность минимального множества отрицательной внешней устойчивости
Число отрицательной внешней устойчивости орграфа – мощность минимального множества отрицательной внешней устойчивости  .
Поиск множеств положительной (отрицательной) внешней устойчивости орграфа производится по модифицированной матрице смежности (модификация заключается в добавлении единичной главной диагонали) с помощью покрытия. При этом покрытия столбцов строками порождают все множества положительной внешней устойчивости, а покрытия всех строк столбцами порождают все множества отрицательной внешней устойчивости.
.
Поиск множеств положительной (отрицательной) внешней устойчивости орграфа производится по модифицированной матрице смежности (модификация заключается в добавлении единичной главной диагонали) с помощью покрытия. При этом покрытия столбцов строками порождают все множества положительной внешней устойчивости, а покрытия всех строк столбцами порождают все множества отрицательной внешней устойчивости.
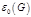 .
Пусть
.
Пусть  - некоторый граф,
- некоторый граф,  - некоторая вершина,
- некоторая вершина, 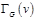 - окрестность вершины
- окрестность вершины  . Неокрестность (коокрестность) вершины
. Неокрестность (коокрестность) вершины  графа
графа 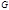 обозначим
обозначим 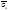 - подграф графа
- подграф графа  , порожденный
, порожденный 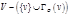 .
Теорема Пустой подграф, содержащий вершину
.
Теорема Пустой подграф, содержащий вершину 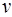 содержит по крайней мере одну вершину из коокрестности вершины
содержит по крайней мере одну вершину из коокрестности вершины  .
Алгоритм нахождения пустых подграфов
Начальный шаг: строится вершина – корень дерева, которой сопоставляется граф
.
Алгоритм нахождения пустых подграфов
Начальный шаг: строится вершина – корень дерева, которой сопоставляется граф  . Итерационный шаг: на
. Итерационный шаг: на 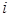 -ом ярусе есть вершина, которой сопоставлен граф
-ом ярусе есть вершина, которой сопоставлен граф 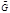 . а) Из
. а) Из  выбирается любая вершина
выбирается любая вершина  ярус. б) На
ярус. б) На  ярус выносятся все вершины, которые входят в
ярус выносятся все вершины, которые входят в 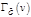 . в) Каждая из вершин
. в) Каждая из вершин 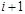 яруса взвешивается соответствующим графом – коокрестностью от графа
яруса взвешивается соответствующим графом – коокрестностью от графа  . Заключительный шаг: вершина дерева будет висячей, если соответствующий ей граф – пустой граф. Замечание В пункте а) желательно выбирать ту вершину, которая имеет минимальную степень.
. Заключительный шаг: вершина дерева будет висячей, если соответствующий ей граф – пустой граф. Замечание В пункте а) желательно выбирать ту вершину, которая имеет минимальную степень.
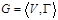 - некоторый граф. Максимальный по включению вершин подграф графа, любые две вершины которого смежны называется полным подграфом. Мощность максимального полного подграфа называется плотностью графа
- некоторый граф. Максимальный по включению вершин подграф графа, любые две вершины которого смежны называется полным подграфом. Мощность максимального полного подграфа называется плотностью графа 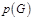 .
Алгоритм нахождения полных подграфов
Начальный шаг: строится вершина – корень дерева, которой сопоставляется граф
.
Алгоритм нахождения полных подграфов
Начальный шаг: строится вершина – корень дерева, которой сопоставляется граф 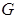 . Итерационный шаг: на
. Итерационный шаг: на 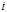 -ом ярусе есть вершина, которой сопоставлен граф
-ом ярусе есть вершина, которой сопоставлен граф 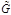 . а) Из
. а) Из 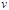 и выносится на
и выносится на 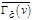 . в) Каждая из вершин
. в) Каждая из вершин  яруса взвешивается соответствующим графом – окрестностью от графа
яруса взвешивается соответствующим графом – окрестностью от графа 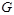 можно свести к задаче нахождения пустых подграфов в
можно свести к задаче нахождения пустых подграфов в  .
.
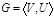 - некоторый граф. Назовем граф
- некоторый граф. Назовем граф  реберным графом
реберным графом 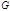 , если носитель графа
, если носитель графа 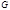 , и две вершины в
, и две вершины в  смежны, если соответствующие ребра смежны в
смежны, если соответствующие ребра смежны в 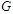 .
Пример
.
Пример
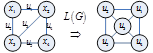 (это преобразование можно выполнить
всегда)
(это преобразование можно выполнить
всегда)
 обладает свойством реберности, если существует некоторый граф, реберный для которого является изоморфным для
обладает свойством реберности, если существует некоторый граф, реберный для которого является изоморфным для 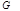 .
.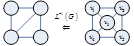
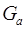 и
и 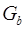 гомеоморфны, если они изоморфны с точностью до цепей степени 2.
Пусть
гомеоморфны, если они изоморфны с точностью до цепей степени 2.
Пусть 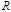 - некоторая поверхность. Род поверхности
- некоторая поверхность. Род поверхности 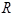 - это максимальное число простых замкнутых кривых, не разделяющих эту поверхность.
Род графа
- это максимальное число простых замкнутых кривых, не разделяющих эту поверхность.
Род графа 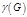 - минимальный род поверхности, на которой можно «уложить» граф
- минимальный род поверхности, на которой можно «уложить» граф 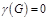 .
печатные платы – планарные графы;
микросхемы (на уровне технологии их изготовления) – планарные графы.
Критерий планарности графа (критерий Понтрягина-Куратовского)
Граф планарен тогда и только тогда, когда в нем отсутствуют подграфы, гомеоморфные
.
печатные платы – планарные графы;
микросхемы (на уровне технологии их изготовления) – планарные графы.
Критерий планарности графа (критерий Понтрягина-Куратовского)
Граф планарен тогда и только тогда, когда в нем отсутствуют подграфы, гомеоморфные 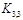 или
или 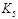 .
Алгоритм приведения графа
.
Алгоритм приведения графа 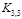 и
и 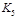 . 2) Построить таблицу покрытия найденных в п.1 подграфов ребрами, которые их образуют. 3) Найти минимальное покрытие подграфов ребрами (удалив ребра, образующие покрытие, получим планарный граф).
. 2) Построить таблицу покрытия найденных в п.1 подграфов ребрами, которые их образуют. 3) Найти минимальное покрытие подграфов ребрами (удалив ребра, образующие покрытие, получим планарный граф).
 - разбиение
- разбиение  на
на 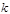 внутренне устойчивых множеств. В этом случае говорят, что вершины графа допускают раскраску в
внутренне устойчивых множеств. В этом случае говорят, что вершины графа допускают раскраску в 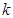 цветов (цвета по номерам
цветов (цвета по номерам  ). Хроматическое число
). Хроматическое число 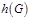 - минимальное значение
- минимальное значение  , которое допускает раскраску графа.
Хроматическое число пустого графа равно 1. Хроматическое число
, которое допускает раскраску графа.
Хроматическое число пустого графа равно 1. Хроматическое число 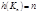 . Хроматическое число
. Хроматическое число 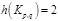 .
Алгоритм нахождения раскраски (хроматического числа)
1) Выделить все пустые подграфы графа. 2) Построить таблицу покрытий вершин графа пустыми подграфами. 3) Найти минимальное покрытие вершин графа пустыми подграфами (мощность минимального покрытия – это
.
Алгоритм нахождения раскраски (хроматического числа)
1) Выделить все пустые подграфы графа. 2) Построить таблицу покрытий вершин графа пустыми подграфами. 3) Найти минимальное покрытие вершин графа пустыми подграфами (мощность минимального покрытия – это 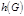 , а само покрытие определяет раскраску).
, а само покрытие определяет раскраску).
 ) тогда и только тогда, когда в
) тогда и только тогда, когда в  , где
, где 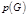 - плотность графа
- плотность графа 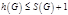 , где
, где 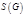 - степень графа
- степень графа  , где
, где 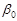 - число внешней устойчивости графа
- число внешней устойчивости графа  , где
, где  ,
,  .
. 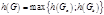 , где
, где 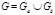 ,
, 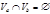 .
. 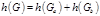 , где
, где  ,
, 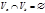 .
. 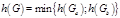 , где
, где  .
Алгоритм приближенной раскраски графа (алгоритм Ершова)
Алгоритм основан на стягивании несмежных вершин:
.
Алгоритм приближенной раскраски графа (алгоритм Ершова)
Алгоритм основан на стягивании несмежных вершин:

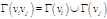 Стягивание проводить до тех пор, пока не получим полный граф. Мощность этого полного графа является оценкой хроматического числа сверху, а сам полный граф определяет приближенную раскраску графа.
Замечание В первую очередь желательно стягивать те вершины, расстояние между которыми четно.
Стягивание проводить до тех пор, пока не получим полный граф. Мощность этого полного графа является оценкой хроматического числа сверху, а сам полный граф определяет приближенную раскраску графа.
Замечание В первую очередь желательно стягивать те вершины, расстояние между которыми четно.
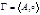 ), которая обладает следующими свойствами:
1) замкнутость
), которая обладает следующими свойствами:
1) замкнутость 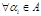 и
и 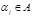
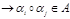 2) ассоциативность
2) ассоциативность 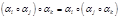 3) наличие нейтрального элемента
3) наличие нейтрального элемента 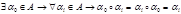 4) существование обратного элемента для
4) существование обратного элемента для 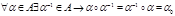 Группа подстановки. Пусть
Группа подстановки. Пусть 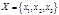 . Подстановкой назовем
. Подстановкой назовем 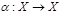 .
.
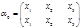


 Операция: произведение подстановок
Операция: произведение подстановок 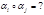


 - это изоморфизм на себя (с, сохраняющая отношение смежности между вершинами графа).
Пример
- это изоморфизм на себя (с, сохраняющая отношение смежности между вершинами графа).
Пример
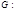

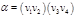 - не является автоморфизмом.
- не является автоморфизмом. 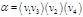 - автоморфизм.
Группа автоморфизмов графа
- автоморфизм.
Группа автоморфизмов графа 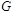 -
- 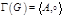 , где
, где  - множество всех автоморфизмов графа,
- множество всех автоморфизмов графа,  - операция произведения.
Пример
- операция произведения.
Пример


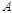 :
:
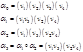
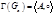 ,
, 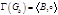 .
. 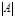 - порядок группы
- порядок группы  ,
, 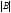 - порядок группы
- порядок группы  . Группа
. Группа  действует на множестве
действует на множестве 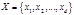 . Группа
. Группа  действует на множестве
действует на множестве 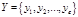 (
(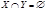 ).
). 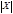 - степень группы
- степень группы  .
.  - степень группы
- степень группы 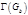 . Рассмотрим три операции над группами:
Сложение (объединение) групп – «
. Рассмотрим три операции над группами:
Сложение (объединение) групп – «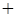 ».
Умножение групп – «
».
Умножение групп – «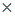 ».
».




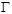 действует на
действует на 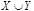
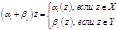
 , порядок
, порядок  равен
равен 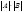
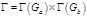
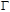 действует на
действует на 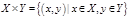
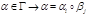

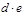 , порядок
, порядок 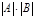 .
.